3.3: Functores, transformaciones naturales y bases de datos
- Page ID
- 112315
En la Sección 3.1 mostramos algunos esquemas de bases de datos: gráficas con ecuaciones de ruta. Entonces en la Sección 3.2.2 dijimos que las gráficas con ecuaciones de trayectoria corresponden a categorías finitamente presentadas. Ahora queremos explicar cuáles son los datos en una base de datos, como una forma de introducir funtores. Para ello, comenzamos notando que conjuntos y funciones los objetos y morfismos en la categoría Set pueden ser capturados por bases de datos particularmente simples.
Conjuntos y funciones como bases de datos
La primera observación es que cualquier conjunto puede entenderse como una tabla con una sola columna: la columna ID.
En lugar de poner los elementos del conjunto entre llaves, e.g. {2, 3, 5, 7, 11,.}, los escribimos como filas en una tabla.
En las bases de datos, las tablas de una sola columna a menudo se denominan vocabularios controlados o datos maestros. Ahora para ser honestos, solo podemos escribir cada entrada en una tabla cuando su conjunto de filas es finito. Un practicante de bases de datos podría encontrar la idea de nuestra tabla de números primos un poco poco realista. Pero somos matemáticos, así que como la idea tiene perfecto sentido de manera abstracta, seguiremos pensando en los conjuntos como tablas de una columna.
Las bases de datos anteriores tienen esquemas que constan de un solo vértice:
Obviamente, realmente no hay mucha diferencia entre estos esquemas, aparte de la etiqueta del vértice único. Entonces podríamos decir “los conjuntos son bases de datos cuyo esquema consiste en un solo vértice”. Pasemos a las funciones.
Una función f: A → B casi se puede representar como una tabla de dos columnas
excepto que no está claro si los elementos de la columna derecha agotan todo B. ¿Y si hay instrumentos de rock and roll que ninguno de los Beatles tocó? Entonces una función f: A → B requiere dos tablas, una para A y su columna f, y otra para B:
Por lo tanto, el esquema de base de datos para cualquier función es solo una versión etiquetada de 2:
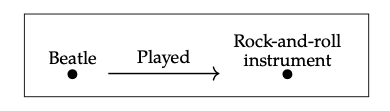
La lección es que una instancia de una base de datos toma una presentación de una categoría, y convierte cada vértice en un conjunto, y cada flecha en una función. Como tal, describe un mapa de la categoría presentada a la categoría Set. En la Sección 2.4.2 vimos que los mapas OFV-categorías son conocidos como V-Functors. De igual manera, llamamos mapas de categorías viejas llanas, funtores.
Funtores
Un functor es un mapeo entre categorías. Envía objetos a objetos y morfismos a morfismos, todo preservando identidades y composición. Aquí está la definición formal.
Que C y D sean categorías. Para especificar un functor de C a D, denotado F: C → D,
i) para cada objeto c\(\in\) Ob (C), se especifica un objeto F (c)\(\in\) Ob (D);
(ii) por cada morfismo f: c 1 → c 2 en C, se especifica un morfismo F (f): F (\(c_{1}\)) → F (\(c_{2}\)) en D.
Los componentes anteriores deben satisfacer dos propiedades:
(a) para cada objeto c\(\in\) Ob (C), tenemos F (\(id_{c}\)) =\(id_{F(c)}\).
b) por cada tres objetos\(c_{1}\),\(c_{2}\),\(c_{3}\)\(\in\) Ob (C) y dos morfismos f\(\in\) C (c 1, c 2), g\(\in\) C (\(c_{2}\),\(c_{3}\)), la ecuación F (f; g ) = F (f); F (f; g) se mantiene en D.
Por ejemplo, aquí dibujamos tres funtores F: 2 → 3:
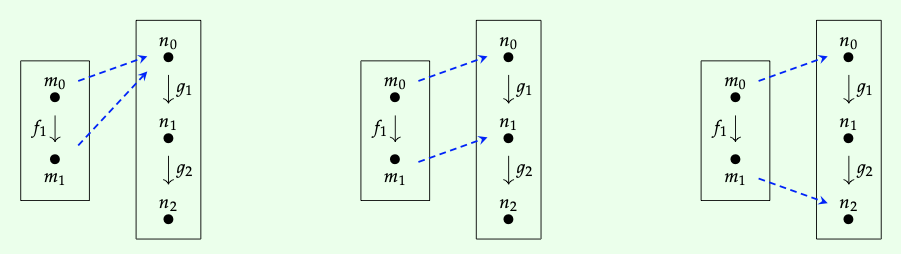
En cada caso, las flechas punteadas muestran lo que el functor F hace a los vértices en 2; una vez que se especifica esa información, resulta en este caso especial que lo que F hace a los tres caminos en 2 está completamente determinado. En el diagrama de la izquierda, F envía cada ruta a la ruta trivial, es decir, la identidad encendida\(n_{0}\). En el diagrama medio F (\(m_{0}\)) =\(n_{0}\), F (\(f_{1}\)) =\(g_{1}\), y F (\(m_{1}\)) =\(n_{1}\). En el diagrama de la derecha, F (\(m_{0}\)) =\(n_{0}\), F (\(m_{1}\)) =\(n_{2}\) y F (\(f_{1}\)) =\(g_{1}\);\(g_{2}\).
Arriba anotamos tres funtores 2 → 3. Encuentra y anota todos los funtores restantes 2 → 3 ♦
Recordemos las categorías presentadas por Free_square y COMM_square en la Sección 3.2.2. Aquí están de nuevo, con' añadido a las etiquetas en Free_square para ayudar a distinguirlos:
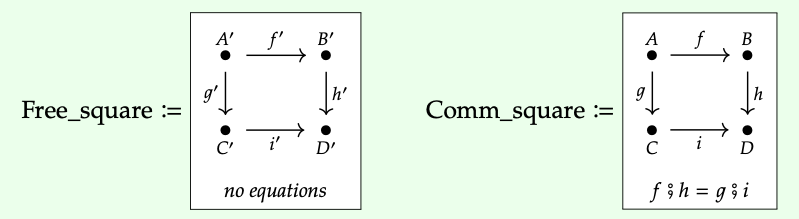
Hay muchos funtores desde la categoría cuadrado libre (llamémoslo F) hasta la categoría cuadrada conmutativa (llamémoslo C).
Sin embargo, hay exactamente un functor F: F → C que envía A ′ a A, B ′ a B, C ′ a C y D ′ a D. Es decir, una vez que hemos tomado esta decisión sobre cómo F actúa sobre los objetos, cada uno de los diez caminos en F se ve obligado a ir a un cierto camino en C: el que tiene la fuente y el objetivo correctos.
Decir a dónde se envía cada uno de los diez morfismos en F bajo el functor F del Ejemplo 3.38. ♦
Todos nuestros funtores de ejemplo hasta el momento han estado completamente determinados por lo que hacen en los objetos, pero este no suele ser el caso.
Considera las categorías gratuitas\(\mathcal{C}=\bullet \rightarrow \bullet \text { and } \mathcal{D}=\bullet \rightrightarrows \bullet\).
Dar dos funtores F, G: C → D que actúan igual sobre los objetos pero de manera diferente sobre los morfismos. ♦
También hay muchos funtores desde la categoría cuadrada conmutativa C hasta la categoría cuadrada libre F, pero ninguno que envíe A a A′, B a B ′, C a C ′ y D a D ′. La razón es que si F fuera tal functor, entonces desde f; h = g; i en C, tendríamos F (f; h) = F (g; i), pero entonces las reglas de los funtores harían razonemos de la siguiente manera:
La ecuación resultante, f'; h' = g '; i' no se sostiene en F porque es una categoría libre (no hay “ecuaciones”): cada dos caminos se consideran morfismos diferentes. Por lo tanto, nuestra F propuesta no es un funtor.
Recordemos de la Sección 3.2.3 que los pedidos por adelantado son categorías con como máximo un morfismo entre dos objetos cualesquiera. Un functor entre preordenes es exactamente un mapa monótona.
Por ejemplo, considere el preorden (\(\mathbb{N}\), ≤) considerado como una categoría N con objetos Ob (N) =\(\mathbb{N}\) y un morfismo único m → n iff m ≤ n. Un functor F: N → N envía cada objeto n\(\in\)\(\mathbb{N}\) a un objeto F (n)\(\in\)\(\mathbb{N}\). Debe enviar morfismos en N a morfismos en\(\mathbb{N}\). Esto significa que si hay un morfismo m → n entonces es mejor que haya un morfismo F (m) → F (n). Es decir, si m ≤ n, entonces mejor tendríamos que tener F (m) ≤ F (n). Pero mientras m ≤ n implique F (m) ≤ F (n), tenemos un functor.
Así un functor F: N → N y un mapa monótona\(\mathbb{N}\) →\(\mathbb{N}\) son lo mismo.
De vuelta en el supurado primordial, existe una categoría Gato en la que los objetos son en sí categorías. Su tarea aquí es construir esta categoría.
1. Dada cualquier categoría C, muestran que existe un functor\(id_{C}\): C → C, conocido como el functor de identidad en C, que mapea cada objeto a sí mismo y cada morfismo a sí mismo.
Tenga en cuenta que un functor C → D consiste en una función de Ob (C) a Ob (D) y para cada par de objetos\(c_{1}\),\(c_{2}\)\(\in\) C una función de C (\(c_{1}\),\(c_{2}\)) a D (\(c_{1}\),\(c_{2}\)).
2. Demostrar que dadas F: C → D y G: D → E, podemos definir un nuevo functor (F; G): C → E simplemente componiendo funciones.
3. Demostrar que hay una categoría, llámala Cat, donde los objetos son categorías, los mor- fismos son funtores, y las identidades y la composición se dan como arriba. ♦
Instancias de base de datos como funtores con valor de conjunto
Que C sea una categoría, y recuerde la categoría Set de Definición 3.24. Set es conocido como un functor de valor establecido en C. Gran parte de la teoría de bases de datos (no cómo hacerlos rápidos, sino qué son y qué haces con ellos) se puede lanzar bajo esta luz. A functor F: C → Set es conocido como un functor de valor establecido en C. De hecho, ya vimos en Observación 3.20 que cualquier esquema de base de datos puede considerarse como (presentando) una categoría C. Lo siguiente a notar es que los datos en sí cualquier instancia de la base de datos están dados por un valor conjunto functor I: C → Set. El único detalle adicional de cadena es que para cualquier nodo blanco, como\(c=\stackrel{\text { string }}{\circ}\), queremos forzar a I a mapear al conjunto de cadenas. Suprimimos este detalle en la siguiente definición.
Sea C un esquema, es decir, una categoría finitamente presentada. Una instancia C es un functor I: C → Set. \(^{5}\)
Que 1 denote la categoría con un objeto, llamado 1, un morfismo de identidad\(id_{1}\), y ningún otro morfismos. Para cualquier functor F: 1 → Set uno puede extraer un conjunto F (1). Mostrar que para cualquier conjunto S, hay un functor\(F_{S}\): 1 → Set tal que\(F_{S}\) (1) = S. ♦
El ejercicio anterior reafirma que el conjunto de planetas, el conjunto de números primos y el conjunto de cerdos voladores son todas instancias funtoras de valores establecidos en el esquema 1. Del mismo modo, los funtores de valor establecido en la categoría 2 son funciones. Todos nuestros ejemplos hasta el momento son para la situación en la que el esquema es una categoría libre (sin ecuaciones). Probemos un ejemplo de una categoría que no es gratuita.
Considere la siguiente categoría:
¿Qué es un functor de valor conjunto F: C → Set? Consiste en un conjunto Z: = F (z) y una función S: = F (s): Z → Z, sujeto al requisito de que S; S = S. Aquí hay algunos ejemplos
• Z es el conjunto de ciudadanos estadounidenses, y S envía a cada ciudadano a ella o a su presidente. El presidente del presidente es ella o él mismo.
• Z =\(\mathbb{N}\) es el conjunto de números naturales y S envía cada número a 0. En particular, 0 va a sí mismo.
• Z es el conjunto de todas las expresiones aritméticas bien formadas, como 13 + (2 ∗ 4) o −5, que se pueden escribir usando números enteros y los símbolos +, −, ∗, (,). La función S evalúa la expresión para devolver un entero, que en sí mismo es una expresión bien formada. La evaluación de un entero es en sí misma.
• Z =\(\mathbb{N}\)\(_{≥2}\), y S envía n a su factor primo más pequeño. El factor primo más pequeño de un primo es en sí mismo.
Arriba, pensamos en el tipo de datos que tendrían sentido para el esquema (3.47). Dé un ejemplo del tipo de datos que tendría sentido para los siguientes esquemas:
La idea principal es esta: un esquema de base de datos es una categoría, y una instancia en ese esquema los datos en sí son un functor de valor establecido. Todas las limitaciones, o reglas de negocio, están aseguradas por las reglas de los funtores, es decir, que los funtores preserven la composición. \(^{6}\)
Transformaciones naturales
Si C es un esquema, es decir, una categoría finitamente presentada entonces hay muchas instancias de base de datos en él, que podemos organizar en una categoría. Pero esto es parte de una historia más amplia, a saber, la de las transformaciones naturales. Una imagen abstracta a tener en mente es la siguiente:
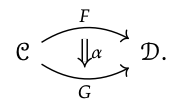
Que C y D sean categorías, y que F, G: C → D sean funtores. Para especificar una transformación natural α: F ⇒ G,
(i) para cada objeto c\(\in\) C, se especifica un morfismo\(α_{c}\): F (c) → G (c) en D, llamado el componente c de α.
Estos componentes deben cumplir lo siguiente, llamado la condición de naturalidad:
(a) por cada morfismo f: c → d en C, debe contener la siguiente ecuación:
F (f);\(α_{d}\) =\(α_{c}\); G (f).
Una transformación natural α: F → G se llama isomorfismo natural si cada componente\(α_{c}\) es un isomorfismo en D.
La condición de naturalidad también se puede escribir como un llamado diagrama conmutativo. Un diagrama en una categoría se dibuja como una gráfica cuyos vértices y flechas están etiquetados por objetos y morfismos en la categoría. Por ejemplo, aquí hay un diagrama que es relevante para la condición de naturalidad en la Definición 3.49:
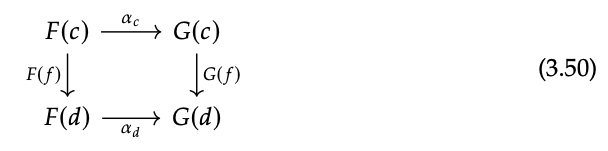
Un diagrama D en C es un functor D: J → C de cualquier categoría J, denominado categoría de indexación del diagrama D. Decimos que D viaja si D (f) = D (f ′) se mantiene por cada par paralelo de morfismos f, f ′: a → b en J.\(^{7}\)
En términos de la Ec. (3.50), el único caso de dos morfismos paralelos es el de F (c) ⇒ G (d), por así decirlo que el diagrama conmuta es decir que F (f)\(α_{c}\);\(α_{d}\) =; G (f) .Esto es exactamente el condición de naturalidad de la Definición 3.49.
Una imagen representativa es la siguiente:
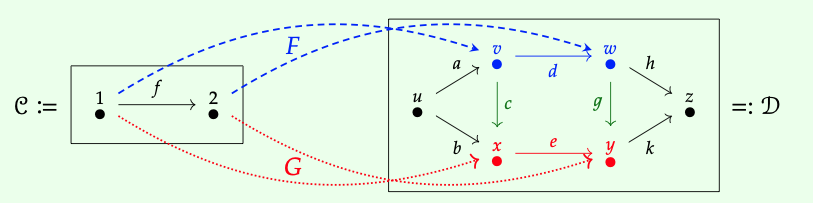
Hemos representado, en azul y rojo respectivamente, dos funtores F, G: C → D. Una transformación natural α: F ⇒ G se da eligiendo componentes\(α_{1}\): v → x y\(α_{2}\): w → y. Hemos resaltado la única opción para cada uno en verde; es decir,\(α_{1}\) = c y\(α_{2}\) = g.
El punto clave es que los funtores F y G son formas de ver la categoría C como que se encuentra dentro de la categoría D. La transformación natural α, entonces, es una forma de relacionar estas dos visiones usando los morfismos en D. ¿Esto te ayuda a ver y apreciar la notación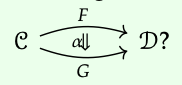 
Dijimos en el Ejercicio 3.45 que un functor 1 → Set se puede identificar con un conjunto. Entonces supongamos que A y B son conjuntos considerados como funtores A, B: 1 → Conjunto. Una transformación natural entre estos funtores es solo una función entre los conjuntos.
Que C y D sean categorías. Denotamos por\(D^{C}\) la categoría cuyos objetos son los funtores F: C → D y cuyos morfismos\(D^{C}\) (F, G) son las transformaciones naturales α: F → G. Esta categoría\(D^{C}\) se llama la categoría functor, o la categoría de funtores de C a D.
Veamos más a fondo cómo\(D^{C}\) es una categoría.
1. Averiguar cómo componer transformaciones naturales. (Pista: un experto te dice “para cada objeto c\(\in\) C, componga los c -componentes.”)
2. Proponer una transformación natural de identidad sobre cualquier objeto F\(\in\) \(D^{C}\), y verificar que es unital (es decir, que obedece a la condición (a) de la Definición 3.6) . ♦
En nuestro nuevo lenguaje, el Ejemplo 3.53 dice que\(Set^{1}\) es equivalente a Set.
Que N denote la categoría asociada al preorden (\(\mathbb{N}\), ≤), y recordemos del Ejemplo 3.42 que podemos identificar un funtor F: N → N con una secuencia no decreciente (\(F_{0}\), \(F_{1}\), \(F_{2}\),...) de números naturales, es decir\(F_{0}\) ≤\(F_{1}\) ≤ \(F_{2}\)≤ ···. Si G es otro functor, considerado como una secuencia no decreciente, entonces ¿qué es una transformación natural α: F → G? Como hay a lo sumo un morfismo entre dos objetos en un preorden, cada componente\(a_{n}\):\(F_{n}\) → no\(G_{n}\) tiene datos, simplemente nos dice un hecho: que\(F_{n}\) ≤\(G_{n}\). Y la condición de naturalidad es vaga: cada plaza en un preorden conmuta. Entonces existe una transformación natural entre F y G iff\(F_{n}\) ≤\(G_{n}\) para cada n, y cualesquiera dos transformaciones naturales F ⇒ G son las mismas. En otras palabras, la categoría\(N^{N}\) es en sí misma un preorden; es decir, el preorden de mapas monótonos\(\mathbb{N}\) →\(\mathbb{N}\).
Que C sea una categoría arbitraria y que P sea una preorden, pensada como una categoría. Considera las siguientes afirmaciones:
1. Para dos funtores cualesquiera F, G: C → P, hay como mucho una transformación natural F → G.
2. Para dos funtores cualesquiera F, G: P → C, hay como mucho una transformación natural F → G.
Para cada uno, si es cierto, digan por qué; si es falso, den un contraejemplo. ♦
OBSERVACIÓN 3.59. Recordemos que en Observación 2.71 dijimos que la categoría de preordenes es equivalente a la categoría de Bool -categorías. Ahora podemos exponer el significado preciso de esta frase. Primero, existe una categoría ProP en la que los objetos son preordenes y los morfismos son mapas monótonos. Segundo, existe una categoría Bool - Cat en la que los objetos son Bool -categorías y los morfismos son Bool -functores. Llamamos a estas dos categorías equivalentes porque existen los funtores F: ProP → Bool - Cat y G: Bool - Cat → ProP tal que existen isomorfismos naturales F; G\(\cong\)\(id_{PrO}\) y G; F\ (\ cong\)\(id_{Bool-Cat}\) en el sentido de la Definición 3.49.
La categoría de instancias en un esquema
Supongamos que C es un esquema de base de datos e I, J: C → Set son instancias de base de datos. Una instancia de homomorfismo entre ellos es una transformación natural α: I → J. Escribe C- Inst :=\(Set^{C}\) para denotar la categoría del functor como se define en la Definición 3.54.
Vimos en el Ejemplo 3.53 que 1 - Inst es equivalente a la categoría Set. En esta subsección, mostraremos que existe un esquema cuyas instancias son gráficas y cuyos homomorfismos de instancia son homomorfismos gráficos.
Ejemplo extendido: la categoría de gráficos como categoría functor. Es posible que te encuentres de nuevo en el supurado primordial (discutido primero en la Sección 2.3.2), porque mientras anteriormente hemos estado usando gráficas para presentar categorías, ahora obtenemos gráficas ellas mismas como instancias de base de datos en un esquema específico (que es a su vez una gráfica):
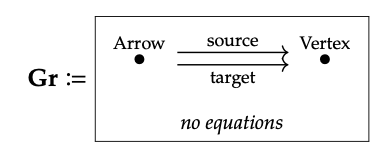
Aquí hay un ejemplo de Gr -instance, es decir, el functor de valor establecido I: Gr → Set, en forma de tabla:
Aquí I (Flecha) = {a, b, c, d, e}, y I (Vértice) = {1, 2, 3, 4}. Se puede dibujar la instancia I como gráfica:
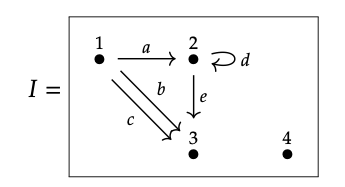
Cada fila de la tabla Vértice se dibuja como un vértice, y cada fila de la tabla Flecha se dibuja como una flecha, conectando su origen y destino especificados. Cada gráfico posible se puede escribir como una instancia de base de datos en el esquema Gr, y cada instancia Gr posible se puede representar como una gráfica.
En la Ec. (3.2), se muestra una gráfica (olvídate de la distinción entre nodos blanco y negro). Anote la instancia Gr correspondiente, como en la Ec. (3.61). (No te preocupes que estés en el supuro primordial. ♦
Así los objetos de la categoría Gr - Inst son gráficos. Los morfismos en Gr - Inst se denominan homomorfismos gráficos. Vamos a desenrollar esto. Supongamos que G, H: Gr → Set son functores (es decir, Gr -instancias); es decir, son objetos G, H\(\in\) Gr - Inst. Un morfismo G → H es una transformación natural α: G → H entre ellos; ¿qué implica eso?
Por Definición 3.49, dado que Gr tiene dos objetos, α consta de dos componentes,
\(α_{Vertex}\): G (Vértice) → H (Vértice) y\(α_{Arrow}\): G (Flecha) → H (Flecha),
ambos de los cuales son morfismos en Set. En otras palabras, α consiste en una función de vértices de G a vértices de H y una función de flechas de G a flechas de H. Para que estas funciones constituyan un homomorfismo gráfico, deben “respetar la fuente y el objetivo” en el sentido preciso que sostiene la condición de naturalidad, Ec. (3.50). Es decir, por cada morfismo en Gr, es decir, origen y destino, los siguientes diagramas deben conmutar:
Estos pueden parecer complicados, pero dicen exactamente lo que queremos. Queremos las funciones\(α_{Vertex}\) y\(α_{Arrow}\) respetar la fuente y los objetivos en G y H. El diagrama de la izquierda dice “comenzar con una flecha en G. Puedes aplicar α a la flecha y luego tomar su fuente en H, o puedes tomar su fuente en G y luego aplicar α a ese vértice; de cualquier manera obtienes la misma respuesta”. El diagrama de la derecha dice lo mismo de los objetivos.
Considere las gráficas G y H que se muestran a continuación
Aquí están, escritos como instancias de bases de datos —es decir, funtores de valor conjunto— en Gr:
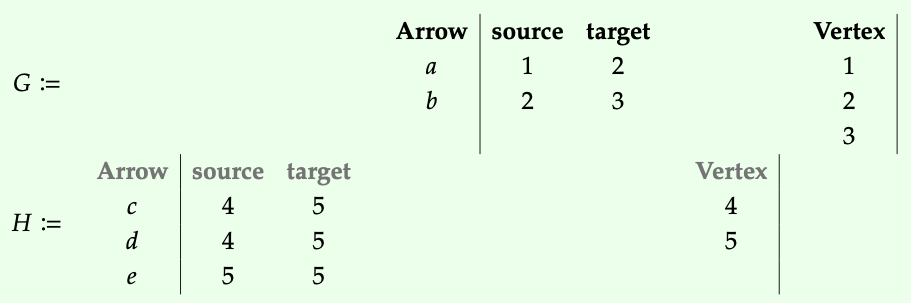
La fila superior es G y la fila inferior es H. Están compensadas para que puedas completar más fácilmente el siguiente ejercicio.
Afirmamos que con G, H como en el Ejemplo 3.63 hay exactamente una gráfica homomorfismo α: G → H tal que\(α_{Arrow}\) (a) = d.
- ¿Cuál es el otro valor de\(α_{Arrow}\), y cuáles son los tres valores de\(α_{Vertex}\)?
- En su propia copia de las tablas del Ejemplo 3.63, dibuje\(α_{Arrow}\) como dos líneas conectando las celdas en la columna ID de G (Flecha) a las de la columna ID de H (Flecha). Del mismo modo, dibuje\(α_{Vertex}\) como líneas de conexión.
- Verifique la columna de origen y la columna de destino y asegúrese de que las coincidencias sean naturales, es decir, que “alfa luego fuente es igual a fuente y luego alfa” y de manera similar para “objetivo. ” ♦