3.4: Adjunciones y migración de datos

Última actualización
Guardar como PDF

Page ID: 112302

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos hablado de cómo los funtores de valor establecido en un esquema pueden entenderse como llenar ese esquema con datos. Pero también hay funtores entre esquemas. Cuando se componen los dos tipos de funtores, los datos se migran. Esta es la forma más simple de migración de datos; formas más complejas de migrar datos provienen del uso de uniones. Todo lo anterior es el tema de esta sección.

Retirar datos a lo largo de un functor

Para comenzar, migraremos datos entre el esquema de indexación gráfica Gr y el esquema de bucle, al que llamamos DDS, que se muestra a continuación

$Screen Shot 2021-01-12 a las 4.37.23 PM.png$

Comenzamos por anotar una instancia de muestra I: DDS → Establecer en este esquema:

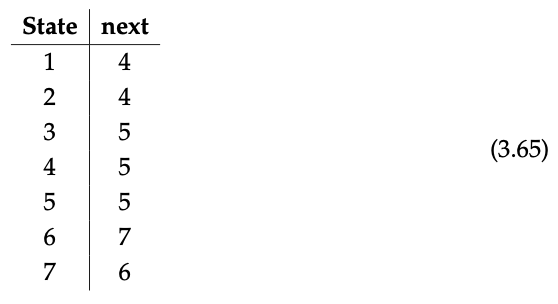
$Screen Shot 2021-01-12 a las 4.37.59 PM.png$

Llamamos al esquema DDS para que signifique sistema dinámico discreto. De hecho, podemos pensar en los datos en la instancia DDS de la Ec. (3.65) como una lista de los estados y movimientos de una máquina determinista: en cada punto en el tiempo la máquina está en uno de los estados enumerados, y dada la máquina en uno de los estados, en el siguiente instante se mueve a un siguiente determinado de manera única estado.

Nuestro objetivo es migrar los datos en la Ec. (3.65) a datos sobre Gr; esto nos dará los datos de una gráfica y así nos permitirá visualizar nuestra máquina.

Utilizaremos un functor que conecte estos esquemas para mover datos entre ellos. El lector puede crear cualquier functor que le guste, pero usaremos un functor específico F: Gr → DDS para migrar datos de una manera que tenga sentido para nosotros, los autores. Aquí dibujamos F, usando colores para, con suerte, ayudar a comprender:

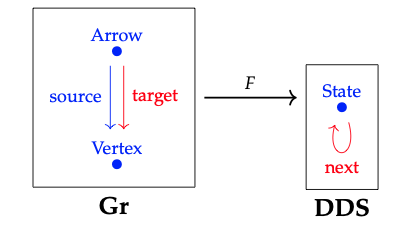
$Screen Shot 2021-01-12 en 4.38.37 PM.png$

El functor F envía ambos objetos de Gr al objeto 'Estado' de DDS (como debe). Sobre los morfismos, envía el morfismo 'fuente' al morfismo identitario sobre 'Estado', y el morfismo 'blanco' al morfismo 'próximo'.

Se dio una instancia de base de datos de muestra en DDS en la Ec. (3.65); recuerde que este es un functor I: DDS → Set. Entonces ahora tenemos dos funtores de la siguiente manera:

$\mathbf{G r} \stackrel{F}{\longrightarrow} \mathbf{D D S} \stackrel{I}{\longrightarrow} \text { Set. }$(3.66)

Los objetos en Gr son enviados por F a objetos en DDS, los cuales son enviados por I a objetos en Set, que son conjuntos. Los morfismos en Gr son enviados por F a morfismos en DDS, los cuales son enviados por I a morfismos en Set, que son funciones. Esto define un functor compuesto F; I: Gr → Set. Tanto F como yo respetamos las identidades y la composición, así que F; yo también. Así hemos obtenido una instancia sobre Gr, es decir, ¡hemos convertido nuestro sistema dinámico discreto de la Ec. (3.65) en una gráfica! ¿Qué gráfica es?

Para una instancia en Gr, necesitamos llenar una tabla Flecha y una tabla Vertex. Ambas son enviadas por F a Estado, así que llenemos ambas con las filas de Estado en la Ec. (3.65). De igual manera, como F envía 'fuente' a la identidad y envía 'target' a 'next', obtenemos las siguientes tablas:

$Screen Shot 2021-01-12 en 4.46.55 PM.png$

Ahora que tenemos una gráfica, la podemos dibujar.

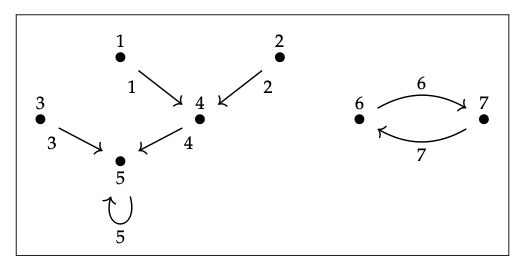
$Screen Shot 2021-01-12 a las 4.49.11 PM.png$

Cada flecha está etiquetada por su vértice fuente, como si dijera: “Lo que hago a continuación está determinado por lo que soy ahora”.

Ejercicio 3.67.

Considera el functor G: Gr → DDS dado enviando 'fuente' a 'siguiente' y enviando 'target' a la identidad en 'Estado'. Migrar los mismos datos, llamados I en la Ec. (3.65), usando el functor G. Anote las tablas y dibuje la gráfica correspondiente. ♦

Nos referimos al procedimiento anterior, básicamente simplemente componiendo funtores como en la Ec. (3.66) como “retroceder datos a lo largo de un functor”. Justo ahora sacamos datos I a lo largo del functor F.

Definición: 3.68.

Que C y D sean categorías y que F: C → D sea un functor. Para cualquier functor de valor establecido I: D → Set, nos referimos al functor compuesto F; I: C → Establecer como el retroceso de I a lo largo de F.

Dada una transformación natural α: I ⇒ J, hay una transformación natural$α_{F}$: F; I ⇒ F; J, cuyo componente (F; I) (c) → (F; J) (c) para cualquier c$\in$ Ob (C) viene dado por ($α_{F}$)$_{c}$ :=$α_{Fc}$

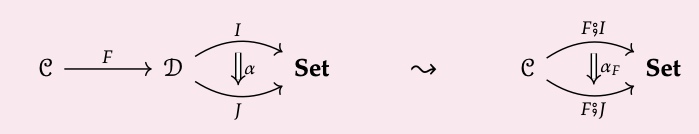
$Screen Shot 2021-01-12 a las 5.10.51 PM.png$

Esto utiliza los datos de F para definir un funtor ∆F: D- Inst → C- Inst.

Tenga en cuenta que el término pullback también se usa para cierto tipo de límite, para más detalles consulte Observación 3.100.

Adjunciones

En la Sección 1.4 discutimos las conexiones Galois, que son adjuntos entre pre- órdenes. Ahora que hemos definido categorías y funcionantes, podemos discutir adjuntos en general. La relevancia para las bases de datos es que el functor migratorio de datos de Defi- nición 3.68 siempre tiene dos anexos propios: un colindante izquierdo que denotamos σ y otro colindante derecho que denotamos π.

Recordemos que un adjunction entre preordenes P y Q es un par de mapas monótonos f: P → Q y g: Q → P que son casi inversos: tenemos

f (p) ≤ q si y sólo si p ≤ g (q). (3.69)

Recordemos de la Sección 3.2.3 que en un preorden P, un hom-set P (a, b) tiene un elemento cuando a ≤ b, y ningún elemento de otra manera. Podemos así replantear la Eq. (3.69) como un isomorfismo de conjuntos Q (f (p), q)$\cong$ P (p, g (q)): o ambos son conjuntos de un elemento o ambos son conjuntos de 0-elementos. Esto sugiere cómo definir adjuntos en el caso general.

Definición: 3.70.

Que C y D sean categorías, y L: C → D y R: D → C sean funtores. Decimos que L se deja unido a R (y que R es derecho contiguo a L) si, para cualquier c$\in$ C y d$\in$ D, hay un isomorfismo de hom-sets

$\alpha_{c, d}: \mathcal{C}(c, R(d)) \stackrel{\cong}{\rightarrow} \mathcal{D}(L(c), d)$

eso es natural en c y d. $^{8}$

Dado un morfismo f: c → R (d) en C, su imagen g :=$α_{c,d}$ (f) se llama su pareja. De igual manera, el mate de g: L (c) → d es f.

Para denotar un exhorto escribimos L R, o en diagramas,

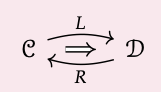
$Screen Shot 2021-01-12 a las 5.12.21 PM.png$

con el ⇒ en dirección a la izquierda colindante.

Ejemplo 3.71.

Recordemos que cada preorden P puede considerarse como una categoría. Las conexiones de Galois entre preordenes y adjuntos entre las categorías correspondientes son exactamente lo mismo.

Ejemplo 3.72.

Deje que B$\in$ Ob (Set) sea cualquier conjunto. Hay un exhorto llamado 'Curry B', después del lógico Haskell Curry:

$Screen Shot 2021-01-12 a las 5.17.23 PM.png$

De manera abstracta lo escribimos como a la izquierda, pero lo que esto significa es que para cualquier conjunto A, C, hay un isomorfismo natural como a la derecha.

Para explicar esto, necesitamos hablar de objetos exponenciales en Set. Supongamos que B y C son conjuntos. Entonces el conjunto de funciones B → C también es un conjunto; vamos a denotarlo C B. Está escrito de esta manera porque si C tiene 10 elementos y B tiene 3 elementos entonces C B tiene 103 elementos, y más generalmente para dos conjuntos finitos cualesquiera |$C^{B}$ | = |C|$_{|B|}$.

La idea de currying es que dados los conjuntos A, B y C, hay una correspondencia uno a uno entre las funciones (A × B) → C y las funciones A →$C^{B}$. Intuitivamente, si tengo una función f de dos variables a, b, puedo “posponir” ingresar a la segunda variable: si me das solo a, devolveré una función B → C que está esperando la entrada B. Esta es la versión al curry de f. Como se podría adivinar, existe una conexión formal entre los objetos exponenciales y lo que llamamos hom-elements b -o c en la Definición 2.79.

Ejercicio 3.73.

En el Ejemplo 3.72, discutimos un adjunction entre los funtores − × B y$(−)^{B}$. Pero sólo dijimos cómo funcionaban estos funtores en los objetos: para un conjunto arbitrario X, devuelven conjuntos X × B y X$^{B}$ respectivamente.

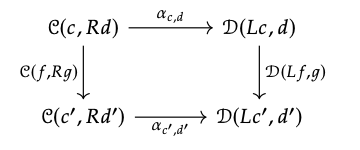
$Screen Shot 2021-01-12 a las 5.22.52 PM.png$

Ante un morfismo f: X → Y, ¿qué morfismo debería − × B: X × B → Y × B regresar?
Ante un morfismo f: X → Y, ¿qué morfismo debería (−)$^{B}$:$^X_{B}$ →$Y^{B}$ regresar?
Considera la función +:$\mathbb{N}$ ×$\mathbb{N}$ →$\mathbb{N}$, que envía (a, b) → a + b. Curriendo +, obtenemos cierta función p:$\mathbb{N}$ →$\mathbb{N}$$^{\mathbb{N}}$. ¿Qué es p (3)? ♦

Ejemplo 3.74.

Si conoces algún álgebra o topología abstracta, aquí hay algunos otros ejemplos de adjuntos.

Construcciones libres: dado cualquier conjunto obtienes un grupo gratis, monoide libre, anillo libre, espacio vectorial libre, etc.; cada uno de estos es un colindante izquierdo. El adjunto derecho correspondiente toma un grupo, un monoide, un anillo, un espacio vectorial, etc. y olvida la estructura algebraica para devolver el conjunto subyacente.
De igual manera, se da agrafreepreordenororafreecategoría, como se discutió en la Sección 3.2.3; cada uno es un adjunto a la izquierda. El derecho adjunto correspondiente es la gráfica subyacente de una preorden o de una categoría.
Cosas discretas: dado cualquier conjunto se obtiene un preorden discreto, gráfico discreto, espacio métrico discreto, categoría discreta, espacio topológico discreto; cada uno de estos es un adjunto izquierdo. El adjunto derecho correspondiente vuelve a ser conjunto subyacente.
Cosas codiscretas: dado cualquier conjunto obtienes un preorden codiscreto, un grafo completo, una categoría codiscreta, un espacio topológico codiscreto; cada uno de estos es un derecho contiguo. El adjunto izquierdo correspondiente es el conjunto subyacente.
Dado un grupo, se puede cociente por su subgrupo conmutador para obtener un grupo abeliano; este es un colindante izquierdo. El derecho adjunto es la inclusión de grupos abelianos en grupos.

Functores de avance izquierdo y derecho,$\Sigma$ y π

Dado F: C → D, el functor de migración de datos ∆F convierte las instancias D en instancias C. Este functor tiene un lado izquierdo y otro derecho colindantes:

$Screen Shot 2021-01-12 at 5.32.03 PM.png$

El uso de los nombres$\Sigma$ y π en este contexto es bastante estándar en la teoría de categorías. En el caso de las bases de datos, tienen los siguientes mnemotécnicos útiles:

$Screen Shot 2021-01-12 at 5.32.48 PM.png$

Al igual que usamos ∆F para retroceder cualquier sistema dinámico discreto a lo largo de F: Gr → DDS y obtener una gráfica, los funtores de migración σ F y π F se pueden usar para convertir cualquier gráfico en un sistema dinámico discreto. Es decir, dada una instancia J: Gr → Set, podemos obtener instancias$\Sigma$ F (J) y Π F (J) en DDS. Esto, sin embargo, es bastante técnico, y dejamos que el lector aventurero calme un ejemplo, con ayuda quizás de [Spi14a], que explora en detalle las definiciones de σ y π. Un atajo menos técnico es simplemente codificar el cálculo en el software FQL de código abierto.

Para dar a conocer la idea básica sin meternos en detalles técnicos, aquí discutiremos en cambio un ejemplo muy sencillo. Recordemos los esquemas de la Ec. (3.5). Podemos configurar un functor entre ellos, el que envía puntos negros a puntos negros y puntos blancos a puntos blancos:

$Screen Shot 2021-01-12 a las 5.36.07 PM.png$

Con este functor F en la mano, podemos transformar cualquier instancia B en una instancia A usando ∆F. Mientras que en la Sección 3.4.1 resultó interesante el caso de convertir sistemas dinámicos discretos en gráficas, no es muy interesante en este caso. De hecho, solo copiará a un duplicado: las filas en el asiento de la aerolínea tanto en Economy como en First Class.

∆F tiene dos anexos,$\Sigma$ F y Π F, los cuales transforman cualquier instancia A I en una instancia B. El functor$\Sigma$ F hace lo que más cabría esperar de leer los nombres en cada objeto: pondrá en Airline Seat la unión de Economy y First Class:

$\sigma$F (I) (Asiento de Aerolínea) = I (Económico) I (Primera Clase).

El functor π F pone en Airline Seat el conjunto de esos pares (e, f) donde e es un asiento Economy, f es un asiento de Primera Clase, y e y f tienen el mismo precio y posición.

En este ejemplo particular, se imagina que no debería haber tales asientos en una instancia válida I, en cuyo caso Π F (I) (Asiento de aerolínea) estaría vacío. Pero en otros usos de estos mismos esquemas, π F puede ser una operación útil. Por ejemplo, en el esquema A reemplace la etiqueta 'Economy' por 'Programa de Recompensas', y en B reemplace 'Asiento de Aerolínea' por 'Asientos de Primera Clas'. Entonces la operación π F encuentra aquellos asientos de primera clase que también son asientos del programa de recompensas. Esta operación es una especie de consulta de base de datos; la consulta es la operación para la que se construyen las bases de datos.

La moraleja es que las migraciones de datos complejas pueden especificarse construyendo los funtores F entre esquemas y usando los funcionadores “inducidos” $\Sigma$F, F y Π F. De hecho, en la práctica esencialmente todas las migraciones útiles se pueden construir a partir de estas. De ahí que el lenguaje de las categorías proporcione un marco para especificar y razonar sobre las migraciones de datos.

Resúmenes de bases de datos de un solo conjunto

Para dar una idea más fuerte del sabor de$\Sigma$ y π, consideramos otro caso especial, a saber, donde la categoría objetivo D es igual a 1; ver Ejercicio 3.12. En este caso, hay exactamente un functor C → 1 para cualquier C; vamos a denotarlo

! : C → 1. (3.75)

Ejercicio 3.76.

¡Describa al funtor! : C → 1 de la Ec. (3.75). ¿A dónde envía cada objeto? ¿Qué pasa con cada morfismo? ♦

¡Queremos considerar los funtores de migración de datos$\Sigma$! : C- Inst → 1 - Inst y π! : C- Inst → 1 - Inst. En el Ejemplo 3.53, vimos que una instancia en 1 es lo mismo que un conjunto. Así que identifiquemos 1 - Inst con Set, y por lo tanto discutamos

$\Sigma$! : C- Inst → Set y π! : C- Inst → Set.

Dado cualquier esquema C e instancia I: C → Set, ¡obtendremos conjuntos$\Sigma$! (I) y Π! (I). Pensando en estos conjuntos como instancias de base de datos, cada uno corresponde a una sola tabla de una columna un vocabulario controlado que resume una instancia de base de datos completa en el esquema C.

Considera el siguiente esquema

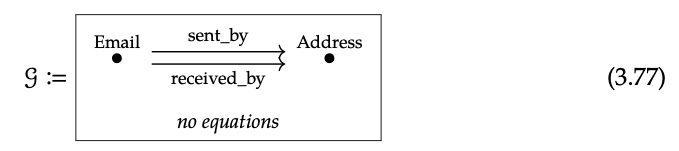
$Screen Shot 2021-01-12 a las 5.51.57 PM.png$

Aquí hay una instancia de muestra I: G → Set:

$Screen Shot 2021-01-12 a las 5.52.51 PM.png$

Ejercicio 3.78.

Obsérvese que G de la Ec. (3.77) es isomórfica al esquema Gr. En la Sección 3.3.5 vimos que las instancias sobre Gr son gráficas.

Dibuja la anterior instancia I como gráfica. ♦

¡Ahora tenemos un functor único! : G → 1, ¡y queremos decir qué$\Sigma$! (I) y Π! (I) darnos como resúmenes de un solo conjunto. Primero,$\Sigma$! (I) nos dice a todos los grupos de correo electrónico los “componentes conectados” en I:

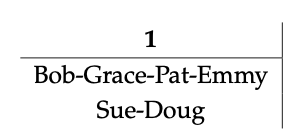
$Screen Shot 2021-01-12 at 6.01.42 PM.png$

Esta forma de resumen, que implica identificar entradas en grupos comunes, o cocientes, es típica de$\Sigma$ -operaciones. El functor π! (I) enumera los correos electrónicos de I que fueron enviados por una persona a ella o a sí mismo.

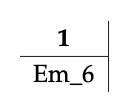
$Screen Shot 2021-01-12 a las 6.02.37 PM.png$

Esto vuelve a ser una especie de consulta, seleccionando las entradas que se ajustan al criterio de los correos electrónicos de uno mismo. Nuevamente, esto es típico de las π-operaciones.
¿Dónde están estos hechos, ese π! y σ! actuar de la manera que decíamos, ¿vienen de? Todo se desprende de la definición de funtores adjuntos (3.70): efectivamente esperamos que esto, junto con los ejemplos dados en el Ejemplo 3.74, den al lector una idea de cuán generales y útiles son las adjuntos, tanto en matemáticas como en teoría de bases de datos.

Un punto más: si bien no vamos a detallar los detalles, observamos que estas operaciones son también ejemplos de construcciones conocidas como colímites y límites en Set. Terminamos este capítulo con material bonus, explorando estas construcciones teóricas de categoría clave. El lector debe tener en cuenta que, en general y no solo para los funtores a 1, las operaciones σse construyen a partir de corlimits en Set, y π-operaciones se construyen a partir de límites en Set.