3.5: Bonificación- Una introducción a los límites y colímites
- Page ID
- 112314
¿Qué hacen los productos de conjuntos, los resultados de π -operaciones en instancias de base de datos, y cumple! en un preorden todos tienen en común? La respuesta, como veremos, es que todos son ejemplos de límites. De igual manera, uniones disjuntas de conjuntos, los resultados de σ -operaciones en! las instancias de base de datos y las combinaciones en un preorden son todos colímites. Empecemos por los límites. Recordemos que π! toma una instancia de base de datos I: C → Set y la convierte en un conjunto π! (I).
De manera más general, un límite convierte a un functor F: C → D en un objeto de D.
Objetos y productos terminales
Los objetos terminales y los productos son cada uno una especie de límite. Vamos a discutirlos a su vez.
Objetos terminales. El límite más básico es un objeto terminal.
Que C sea una categoría. Entonces un objeto Z en C es un objeto terminal si, para cada objeto C de C, ¡existe un morfismo único! : C → Z.
Dado que este morfismo único existe para todos los objetos en C, decimos que los objetos terminales tienen una propiedad universal.
En Set, cualquier conjunto con exactamente un elemento es un objeto terminal. ¿Por qué? Considera algunos de esos conjuntos {•}. Entonces para cualquier otro conjunto C necesitamos verificar que hay exactamente una función! : C → {•}. Esta función única es la que hace lo único que se puede hacer: mapea cada elemento c\(\in\) C al elemento •\(\in\) {•}.
Sea (P, ≤) un preorden, que z\(\in\) P sea un elemento y que P sea la categoría correspondiente (ver Sección 3.2.3). Mostrar que z es un objeto terminal en P si y solo si es un elemento superior en P: es decir, si y solo si para todos c\(\in\) P tenemos c ≤ z. ♦
Nombra un objeto terminal en la categoría Cat. (Pista: recordar Ejercicio 3.76. ) ♦
No todas las categorías tienen un objeto terminal. Encuentra uno que no lo haga. ♦
Todos los objetos terminales en una categoría C son isomórficos.
Prueba. Este es un argumento estándar simple, pero poderoso. Supongamos que Z y Z ′ son ambos objetos terminales en alguna categoría C. Entonces existen mapas (únicos) a: Z → Z ′ y b: Z ′ → Z. Al componer estos, obtenemos un mapa a; b: Z → Z. Ahora como Z es terminal, este mapa Z → Z debe ser único. Pero también\(id_{Z}\) es tal mapa. Entonces debemos tener a; b =\(id_{Z}\). De igual manera, encontramos que b; a =\(id_{Z'}\). Así a es un isomorfismo, con b inverso. □
Comentario 3.85 (“El límite” vs. “un límite”). No sólo todos los objetos terminales son isomórficos, hay un isomorfismo único entre dos cualesquiera. Por lo tanto, decimos que “los objetos terminales son únicos hasta el isomorfismo único”. Para un teórico de categoría, esto es casi lo mismo que decir “todos los objetos terminales son iguales”. Por lo tanto, a menudo abusamos de la terminología y hablamos de 'el' objeto terminal, en lugar de “un” objeto terminal. Haremos lo mismo para cualquier tipo de límite o colimit, por ejemplo, hablar de “el producto” de dos conjuntos, en lugar de “un producto”. Vimos un fenómeno similar en la Definición 1.81.
Productos. Los productos son un poco más complicados de formalizar que los objetos terminales, pero son familiares en la práctica.
Sea C una categoría, y que X, Y sean objetos en C. Un producto de X e Y es un objeto, denotado X × Y, junto con morfismos\(p_{X}\): X × Y → X y\(p_{Y}\): X × Y → Y tal que para todos los objetos C junto con los morfismos f: C → X y g: C → Y, existe un morfismo único C → X × Y, denotado f, g ⟩, para lo cual se conmuta el siguiente diagrama:
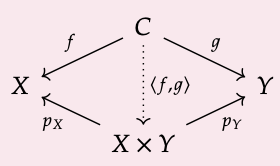
Intentaremos llevar esto a la tierra en el Ejemplo 3.87. Antes de hacerlo, tenga en cuenta que X × Y es un objeto equipado con morfismos a X e Y. En términos generales, es como “el mejor objeto equipado con morfismos a X e Y” en todo C, en el sentido de que cualquier otro objeto equipado con morfismos a X e Y le asigna de manera única. A esto se le llama propiedad universal. Es costumbre usar una línea punteada para indicar el morfismo único que existe por alguna propiedad universal.
En Set, un producto de dos juegos X e Y es su producto cartesiano habitual
X × Y := {(x, y) | x\(\in\) X, y\(\in\) Y},
que viene con dos proyecciones p X: X × Y → X y p Y: X × Y → Y, dadas por\(_{pX}\) (x, y) := x y\(_{pY}\) (x, y) := y.
Dado cualquier conjunto C con funciones f: C → X y g: C → Y, el mapa único de C a X × Y tal que el diagrama requerido se conmuta viene dado por
f, g ⟩ (c) := (f (c), g (c)).
Aquí hay una imagen del producto\(\underline{6}\) ×\(\underline{4}\) de conjuntos\(\underline{6}\) y\(\underline{4}\).
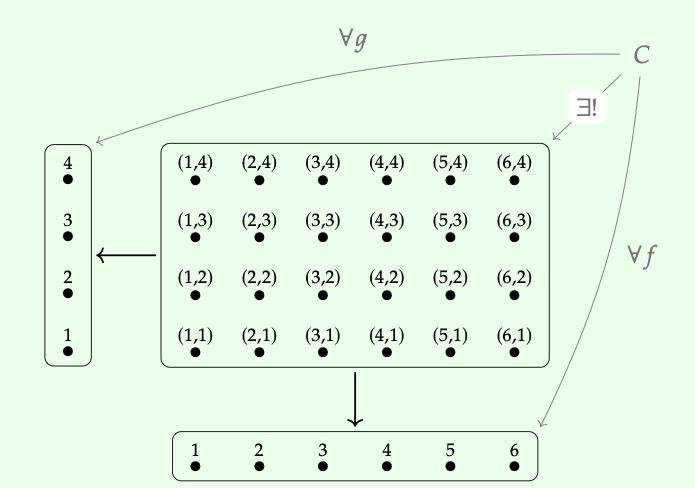
Sea (P, ≤) un preorden, que x, y\(\in\) P sean elementos, y que P sea la categoría correspondiente. Mostrar que el producto x × y en P concuerda con su encuentro x\(\wedge\) y en P. ♦
Dadas dos categorías C y D, su producto C × D se puede dar de la siguiente manera. Los objetos de esta categoría son pares (c, d), donde c es un objeto de C y d es un objeto de D. Del mismo modo, los morfismos (c, d) → (c′, d ′) son pares (f, g) donde f : c → c′ es un morfismo en C y g: d → d ′ es un morfismo en D. La composición de los morfismos se da simplemente componiendo cada entrada en el par por separado, entonces (f, g); (f ′, g ′) = ( f; f ′, g'; g ′).
- ¿Cuáles son los morfismos de identidad en una categoría de producto C × D?
- ¿Por qué la composición en una categoría de producto es asociativa?
- ¿Cuál es la categoría de producto 1 × 2?
- ¿Cuál es la categoría de producto P × Q cuando P y Q son prepedidos y P y Q son las categorías correspondientes? ♦
Estas dos construcciones, objetos terminales y productos, están subsumidos por la noción de límite.
Límites
Nos pondremos un poco abstractos. Considera la definición de producto. Esto dice que dado cualquier par de mapas\(X \leftarrow C \stackrel{g}{\rightarrow} Y\), existe un mapa único C → X × Y tal que ciertos diagramas conmutan. Esto tiene el sabor de ser terminal —hay un mapa único a X × Y —pero parece un poco más complicado. ¿Cómo se relacionan las dos ideas?
Resulta que los productos son objetos terminales, pero de una categoría diferente, que llamaremos Cono (X, Y), la categoría de conos sobre X e Y en C. Veremos en el Ejercicio 3.91 que \(X \stackrel{p_{X}}{\longleftarrow} X \times Y \stackrel{p_{Y}}{\longrightarrow} Y\)es un objeto terminal en Cono (X, Y). Un objeto de Cono (X, Y) es simplemente un par de mapas\(X \stackrel{f}{\longleftarrow} X \times Y \stackrel{g}{\longrightarrow} Y\). Un morfismo de\(X \stackrel{f}{\longleftarrow} X \times Y \stackrel{g}{\longrightarrow} Y\) a\(X \stackrel{f'}{\longleftarrow} X \times Y \stackrel{g'}{\longrightarrow} Y\) en cono (X, Y) isamorfismo a: C → C incsuchQue el siguiente diagrama conmuta:
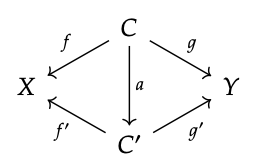
Comprobar que un producto\(X \stackrel{p_{X}}{\longleftarrow} X \times Y \stackrel{p_{Y}}{\longrightarrow} Y\) es exactamente igual que un objeto terminal en Cono (X, Y) . ♦
Ya estamos listos para la definición abstracta. No te preocupes si los detalles no están claros; el punto principal es que es posible unificar objetos terminales, elementos máximos, y meets, productos de conjuntos, preordenes y categorías, y muchos otros amigos familiares bajo el alcance de una sola definición. De hecho, todos son solo objetos terminales en diferentes categorías. Recordemos de la Definición 3.51 que formalmente hablando, un diagrama en C es solo un functor D: J → C. Aquí J se llama la categoría de indexación del diagrama D.
Sea D: J → C un diagrama. Un cono (C, c ∗) sobre D consiste en
i) un objeto C\(\in\) C;
(ii) para cada objeto j\(\in\) J, un morfismo\(c_{j}\): C → D (j).
Para ser un cono, estos deben satisfacer la siguiente propiedad:
(a) por cada f: j → k en J, tenemos\(c_{k}\) =\(c_{j}\); D (f).
Un morfismo de conos (C, c ∗) → (C′, c *′) es un morfismo a: C → C′ en C tal que para todos \(\in\)j J tenemos\(c_{j}\) = a; \(c'_{j}\). Los conos sobre D, y sus morfismos, forman una categoría Cono (D). El límite de D, denotado lim (D), es el objeto terminal en la categoría Cono (D). Digamos que es el cono lim (D) = (C, c ∗); nos referimos a C como el objeto límite y al mapa\(c_{j}\) para cualquier j\(\in\) J como mapa de\(j^{th}\) proyección.
Para fines de visualización, si J es la categoría libre en la gráfica
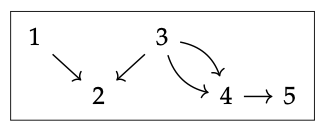
con cinco objetos y cinco morfismos no identitarios, entonces podemos dibujar un diagrama D: J → C dentro de C como a la izquierda de abajo, y un cono sobre él como a la derecha:
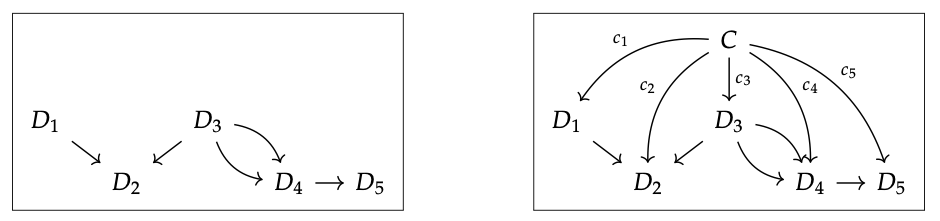
Aquí, dos caminos paralelos cualesquiera que comiencen en C se consideran iguales. Tenga en cuenta que ambos diagramas representan una colección de objetos y morfismos dentro de la categoría C.
Los objetos de borna son límites donde la categoría de indexación está vacía, J = Ø.
Los productos son límites donde la categoría de indexación consta de dos objetos v, w y sin flechas,
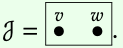
Límites finitos en Set
Recordemos que esta discusión se inspiró en querer entender π-operaciones, y en particular π!. Ya podemos ver que una instancia de base de datos I: C → Set es un diagrama en Set. El functor π! toma el límite de este diagrama. En esta subsección damos una fórmula que describe el resultado. Esto captura todos los límites finitos en Set.
En teoría de bases de datos, se trabaja con categorías C que son presentadas por una gráfica finita más ecuaciones. No vamos a explicar los detalles, pero de hecho basta con trabajar con la parte gráfica: en lo que respecta a los límites, las ecuaciones en C no importan. Para consistencia con el resto de esta sección, denotemos el esquema de la base de datos por J en lugar de C.
Que J sea una categoría presentada por la gráfica finita (V, A, s, t) junto con algunas ecuaciones, y que D: J → Set sea un funtor de valor establecido. Escribir V = {v 1,... , v n}. El conjunto
\ (\ begin {aligned} &\ lim _ {g} D: =\ left\ {\ left (d_ {1},\ ldots, d_ {n}\ right)\ mid d_ {i}\ in D\ left (v_ {i}\ right)\ text {para todos} 1\ leq i\ leq n\ derecho. \ texto {y}\\
&\ texto {para todos} a: v_ {i}\ fila derecha v_ {j}\ en A,\ texto {tenemos}\ izquierda.d (a)\ izquierda (d_ {i}\ derecha) =d_ {j}\ derecha\ derecha\}
\ fin {alineada}\)
junto con los mapas de proyección\(p_{i}\): (\(lim_{J}\)D) → D (v i) dado por\(p_{i}\) (d 1,.., d n) := d i, es un límite de D.
Si J es la gráfica vacía\(\square\), entonces n = 0: no hay vértices. Hay ex- actamente una tupla vacía (), que satisface vacuamente las propiedades, así que hemos construido el límite como el conjunto de singleton {()} que consiste solo en la tupla vacía. Así, el límite del diagrama vacío, es decir, el objeto terminal en Set es el conjunto singleton. Ver Observación 3.85.
Demostrar que la fórmula límite en Teorema 3.95 funciona para productos. Ver Ejemplo 3.94. ♦
Si D: 1 → Set es un functor, ¿cuál es el límite de D? Cómplelo usando el Teorema 3.95, y verifique su respuesta contra la Definición 3.92. ♦
Pullbacks. En particular, la condición de que el límite de D: J → Conjunto seleccione tuplas (d 1,... , d n) tal que D (a) (\(d_{i}\)) = d j por cada morfismo a: i → j en J nos permite usar límites para seleccionar datos que satisfagan ciertas ecuaciones o restricciones. Esto es lo que nos permite expresar consultas en términos de límites. Aquí hay un ejemplo.
Si J es presentado por la gráfica de cospan\(\stackrel{x}{\bullet} \stackrel{f}{\longrightarrow} \stackrel{a}{\bullet} \stackrel{g}{\longleftarrow} y\), entonces su límite se conoce como un retroceso. Dado el diagrama\(X \stackrel{f}{\rightarrow} A \stackrel{g}{\leftarrow} Y\), el retroceso es el cono que se muestra a la izquierda a continuación:

El hecho de que el diagrama conmute significa que la flecha diagonal c a es en cierto sentido superflua, por lo que uno generalmente denota retrocesos al soltar la flecha diagonal, nombrar el punto de cono X ×\(_{A}\) Y, y agregar el\(\text { I }\) símbolo, como que se muestra arriba a la derecha. Aquí hay una imagen para ayudarnos a desempacar la definición en Set. Tomamos X =\(\underline{6}\), Y =\(\underline{4}\), y A para ser el conjunto de colores {rojo, azul, negro}.
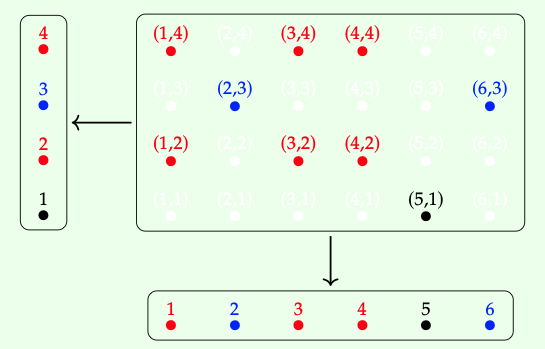
Las funciones f:\(\underline{6}\) → A y g:\(\underline{4}\) → A se expresan en la coloración de los puntos: por ejemplo, g (2) = g (4) = rojo, mientras que f (5) = negro. El pullback selecciona pares (i, j)\(\in\)\(\underline{6}\) × de\(\underline{4}\) tal manera que f (i) y g (j) tengan el mismo color.
OBSERVACIÓN 3.100. Como se menciona a continuación de la Definición 3.68, esta definición de pullback no debe confundirse con el retroceso de un funtor de valor establecido a lo largo de un functor; son por ahora mejor pensados como conceptos diferentes que accidentalmente tienen el mismo nombre. Sin embargo, debido al poder del rezumado primordial, el pullback a lo largo de un functor es un caso especial de pullback como límite de un cospan: puede entenderse como el retroceso de cierto cospan en Cat. Para desempacar esto, sin embargo, se requieren las nociones de categoría de elementos y opfibración discreta; pregúntale a tu amigable teórico de categoría de barrio.
breve nota sobre colímites
Al igual que los límites superiores tienen un concepto dual, es decir, el de los límites inferiores, los límites tienen un concepto dual: los corlímites. Para exponer al lector a este concepto, proporcionamos una definición sucinta de estos utilizando categorías opuestas y funcionantes opuestos. El punto, sin embargo, es solo la exposición; volveremos a explorar los corlímites en detalle en el Capítulo 6.
Recordemos del Ejemplo 3.27 que cada categoría C tiene un Cop opuesto. Que F: C → D sea un funtor. ¿Cómo debemos definir su opuesto, F\(^{op}\): C\(^{op}\) → D\(^{op}\)? Es decir, ¿cómo debería\(^{op}\) actuar F sobre los objetos y cómo debería actuar sobre los morfismos? ♦
Dada una categoría C decimos que un cocono en C es un cono en\(^{op}\) C. Dado un diagrama D: J → C, podemos tomar el límite del functor D\(^{op}\): J\(^{op}\) →\(^{op}\) C.
Este es un cono en C\(^{op}\), y así por definición un cocono en C. El colímite de D es este cocono.
La definición 3.102 es como un archivo comprimido: útil para transmitir rápidamente, pero muy inútil para trabajar con él, a menos que pueda desempaquetarlo con éxito. Lo desempacaremos más adelante en el Capítulo 6 cuando discutamos los circuitos eléctricos.


