4.3: Categorías de Profunctors

Última actualización
Guardar como PDF

Page ID: 112137

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Existe una categoría Feas cuyos objetos son preordenes y cuyos morfismos son relaciones feasi- bles. Para describirlo, debemos dar la fórmula de composición y las identidades, y demostrar que satisfacen las propiedades de ser una categoría: la unidad y la asociatividad.

Profuntores de composición

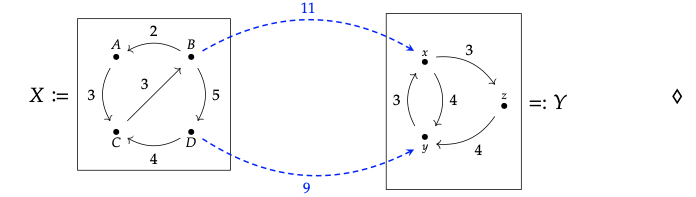
Si las relaciones de factibilidad van a ser morfismos, necesitamos dar una fórmula para componer dos de ellas en serie. Imagina que tienes ciudades P, Q y R y tienes puentes y por lo tanto matrices de factibilidad que conectan estas ciudades, digamos Φ: P → Q y ψ: Q → R.

$Screen Shot 2021-01-17 at 1.58.57 PM.png$

Las matrices de factibilidad para Φ (en azul) y ψ (en rojo) son:

$Screen Shot 2021-01-17 at 1.59.49 PM.png$

Al igual que en la observación 2.95, personificamos una quantale como navegante. Así que imagina que un navegante está tratando de dar una matriz de factibilidad Φ; ψ para pasar de P a R. ¿Cómo se debe hacer esto? Básicamente, por cada par p$\in$ P y r$\in$ R, el navegador busca a través de Q un way-point q, en algún lugar tanto al que podemos llegar desde p Y desde el que podemos llegar a r. Es cierto que podemos navegar de p a r iff hay un way-point q a través del cual transitar; este es un gran OR sobre todo q posible. La fórmula de la composición es así:

$\left(\Phi_{9}^{\circ} \Psi\right)(p, r):=\bigvee_{q \in \mathbb{Q}} \Phi(p, q) \wedge \Psi(q, r)$(4.20)

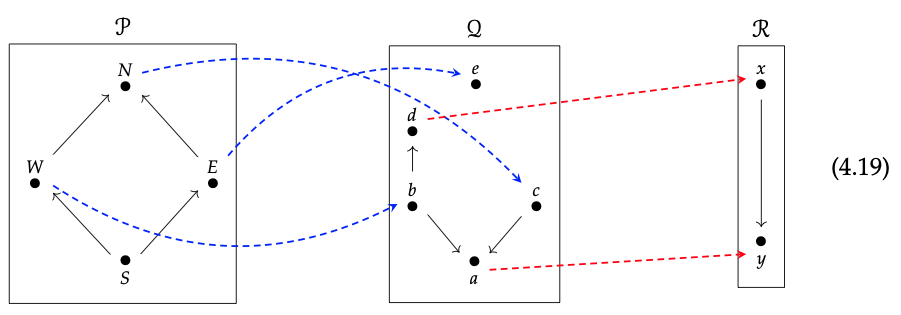
Pero como dijimos en la ecuación (2.101), esto puede pensarse como multiplicación matricial. En nuestro ejemplo, el resultado es

$Screen Shot 2021-01-17 a las 2.00.46 PM.png$

y uno puede comprobar que esto responde a la pregunta, “se puede llegar de aquí para allá” en la Ec. (4.19): no se puede obtener de N a x pero se puede obtener de N a y.

La fórmula (4.20) está escrita en términos de la quantale Bool, pero funciona para quantales arbitrarios (unital conmutativos). Damos la siguiente definición.

Definición: 4.21.

Que V sea una cantidad, que X, Y y Z sean categorías V, y que Φ: X → Y y ψ: Y → Z sean profunctores V.

Definimos su compuesto, denotado Φ; ψ: X → Z por la fórmula

$\left(\Phi_{9} \Psi\right)(p, r)=\bigvee_{q \in Q}(\Phi(p, q) \otimes \Psi(q, r))$

Ejercicio 4.22.

Considere los Profunctores Costo Φ: X → Y y ψ: Y → Z que se muestran a continuación:

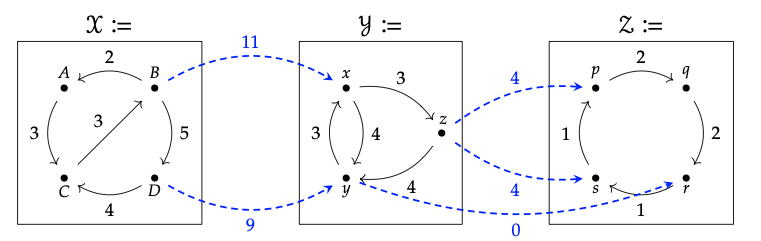
$Screen Shot 2021-01-17 a las 2.06.06 PM.png$

Rellene la matriz para el profunctor compuesto:

$Screen Shot 2021-01-17 a las 2.06.30 PM.png$

Las categorías V - Prof y Feas

Una regla de composición sugiere una categoría, y de hecho hay una categoría donde los objetos son categorías Bool y los morfismos son Bool -profunctors. Para que esto funcione de manera más general, sin embargo, necesitamos agregar una condición técnica.

Recordemos de Observación 1.35 que un preorden es un preorden esquelético si siempre que x ≤ y y ≤ x, tenemos x = y. Los preordenes esqueléticos también se conocen como posets. Decimos que un quantale es esquelético si su preorden subyacente es esquelético; Bool y Cost son quantales esqueléticos.

Teorema 4.23.

Para cualquier quantale esquelético V, existe una categoría Prof$_{V}$ cuyos objetos son categorías V X, cuyos morfismos son Profuntores V X → Y, y con composición definida como en la Definición 4.21.

Definición: 4.24.

Definimos Feas = Prof$_{Bool}$.

En este punto quizás tengas dos preguntas en mente. ¿Cuáles son los morfismos de identidad? ¿Y por qué necesitábamos especializarnos en quantales esqueléticos? Resulta que estas dos preguntas están estrechamente relacionadas.

Definir el profunctor de unidad U$_{X}$: X → X en una categoría V X por la fórmula

U$_{X}$ (x, y) := X (x, y) . (4.25)

¿Cómo interpretamos esto? Recordemos que, por la Definición 2.46, X ya asigna a cada par de elementos x, y$\in$ X un hom-object X (x, y)$\in$ V. El profunctor de unidad UX sólo asigna a cada par (x, y) ese mismo objeto.

En el caso Bool el profunctor de la unidad en algún preorden X se puede dibujar así:

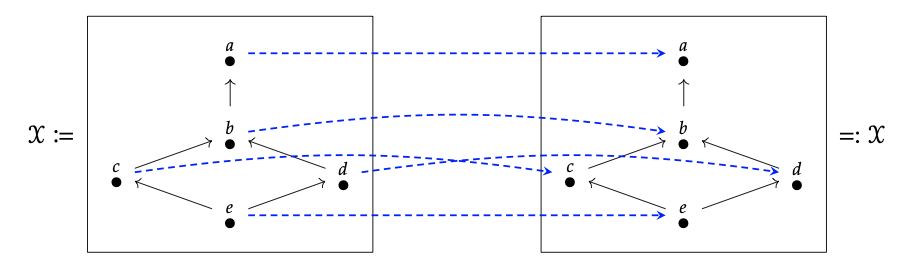
$Screen Shot 2021-01-17 a las 2.14.34 PM.png$

Obviamente, componer una relación de factibilidad con la unidad la deja sin cambios; este es el contenido de Lemma 4.27.

Ejercicio 4.26.

Elija una categoría de costo no muy simple X. Dar un diagrama estilo puente para el profunctor de unidad U$_{X}$: X → X. ♦

Lema 4.27.

Al componer cualquier profunctor Φ: P → Q con el profunctor de unidad, U$_{P}$ o U$_{Q}$, devuelve Φ:

$\mathrm{U}_{\mathcal{P}} \text { ; } \Phi=\Phi=\Phi_{\text {9 }}^{\circ} \mathrm{U}_{\mathrm{Q}}$

Comprobante. Mostramos que U$_{P}$; Φ = Φ sostiene; demostrando Φ = Φ; U$_{Q}$ es similar. Fijar $\in$p P y q$\in$ Q. Dado que V es esquelético, para demostrar la igualdad basta con mostrar Φ ≤ U$_{P}$; Φ y U$_{P}$; Φ ≤ Φ. Tenemos una dirección:

$\Phi(p, q)=I \otimes \Phi(p, q) \leq \mathcal{P}(p, p) \otimes \Phi(p, q) \leq \bigvee_{p_{1} \in P}\left(\mathcal{P}\left(p, p_{1}\right) \otimes \Phi\left(p_{1}, q\right)\right)=\left(\mathrm{U}_{\mathcal{P}} \text { ; } \Phi\right)(p, q)$(4.28)

Para la otra dirección, debemos mostrar$\bigvee_{p1 \(\in$ P}\) (P (p, p) Φ (p, q$_{1}$)) ≤ Φ (p$_{1}$, q)) ≤ Φ (p, q).

Pero por definición de unión, esto sostiene iff P (p, p$_{1}$) Φ (p$_{1}$, q) ≤ Φ (p, q) es cierto para cada p$_{1}$$\in$ P. Esto se desprende de las Definiciones 2.46 y 4.8:

$\mathcal{P}\left(p, p_{1}\right) \otimes \Phi\left(p_{1}, q\right)=\mathcal{P}\left(p, p_{1}\right) \otimes \Phi\left(p_{1}, q\right) \otimes I \leq \mathcal{P}\left(p, p_{1}\right) \otimes \Phi\left(p_{1}, q\right) \otimes 2(q, q) \leq \Phi(p, q)$(4.29)$\square$

Ejercicio 4.30.

Justificar cada uno de los cuatro pasos (=, ≤, ≤, =) en la Ec. (4.28).
En el caso V = Bool, podemos mostrar directamente cada uno de los cuatro pasos en la Ec. (4.28) es en realidad una igualdad. ¿Cómo?
Justificar cada uno de los tres pasos (=, ≤, ≤) en la Ec. (4.29) . ♦

La composición de los profunctores también es asociativa; te dejamos la prueba a ti.

Lema 4.3.1.

La composición serial de los profunctores es asociativa. Es decir, dados los profunctores Φ: P → Q, ψ: Q → R, y: R → S, tenemos

(Φ; Ψ); Y = Φ; (Ψ; Y)

Ejercicio 4.3.2.

Demostrar Lema 4.31. (Pista: recuerda usar el hecho de que V es esquelético. ) ♦

Entonces, las relaciones de factibilidad forman una categoría. Como este es el caso, podemos describir las relaciones de factibilidad utilizando diagramas de cableado para categorías (ver también Sección 4.4.2), que son muy simples. De hecho, cada caja solo puede tener una entrada y una salida, y están conectadas en una línea:

$Screen Shot 2021-01-17 en 2.42.15 PM.png$

Por otro lado, hemos visto que las relaciones de factibilidad son los bloques de construcción de los problemas de co-diseño, y sabemos que los problemas de co-diseño se pueden representar con un diagrama de cableado mucho más rico, por ejemplo:

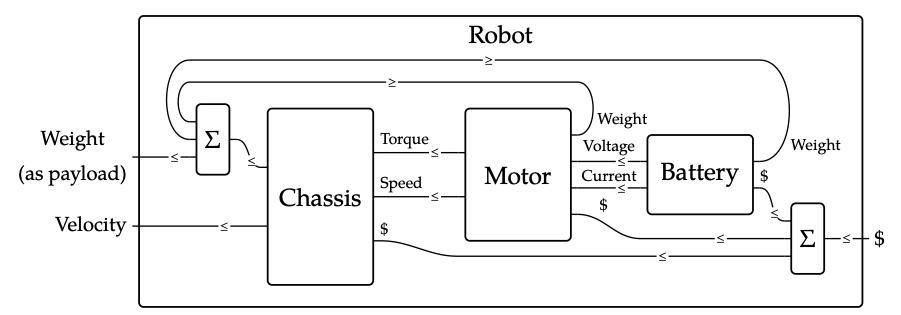
$Screen Shot 2021-01-17 en 2.42.52 PM.png$

Esto insinúa que la categoría Feas tiene más estructura. Hemos visto diagramas de cableado donde las cajas pueden tener múltiples entradas y salidas antes, en el Capítulo 2; allí representaban morfismos en un preorden monoidal. Por otro lado las cajas en los diagramas de cableado del Capítulo 2 no podían tener etiquetas distintas, como las cajas en un problema de co-diseño: todas las cajas en un diagrama de cableado para preordenes monoidales indican el orden ≤, mientras que arriba vemos cajas etiquetadas con “Chasis”, “Motor”, y así sucesivamente. De igual manera, sabemos que Feas es una categoría adecuada, no sólo una preorden. Para entender entonces estos diagramas, debemos introducir una nueva estructura, llamada categoría monoidal. Una categoría monoidal es un preorden monoidal categorizado.

OBSERVACIÓN 4.33. Si bien hemos optado por definir al Prof$_{V}$ solo para quantales esqueléticos en el Teorema 4.23, no es demasiado difícil trabajar con los no esqueléticos. Hay dos formas simples de hacer esto. Primero, podríamos dejar que los morfismos del Prof$_{V}$ sean clases de isomorfismo de profunctores V. Esto es análogo al truco que usaremos al definir la categoría Cospan$_{C}$ en la Definición 6.45. Segundo, podríamos relajar lo que entendemos por categoría, solo requiriendo que la composición sea unital y asociativa 'hasta el isomorfismo'. Este es también un tipo de categorización, conocida como teoría bicategoria.

En la siguiente sección discutiremos la categorización e introduciremos categorías monoidales. Pero primero, terminamos esta sección discutiendo por qué los profunctores son llamados profuntores, y introduciendo formalmente algo llamado collage de un profuntor.

Datos divertidos del profunctor: compañeros, conjuntos, collages

Compañeros y juntas. Recordemos que un preorden es una categoría Bool y un mapa monótono es un Bool -functor. Nosotros dijimos anteriormente que un profunctor es una generalización de un funtor; ¿cómo es así?

De hecho, cada funtor V da lugar a dos profunctores V, llamados el compañero y el conjunto.

Definición: 4.34.

Que F: P → Q sea un funtor V. El compañero de F, denotado$widehat{F}$: P → Q y el conjunto de$widehat{F}$, denotado$\breve{F}$: Q P se definen como los siguientes Profunctores V:

$\widehat{F}(p, q):=Q(F(p), q) \text { and } \breve{F}(q, p):=Q(q, F(p))$

Consideremos de nuevo el caso Bool.

Se puede pensar en un mapa monótono F: P → Q como un manojo de flechas, una que sale de cada vértice p$\in$ P y aterriza en algún vértice F (p)$\in$ Q.

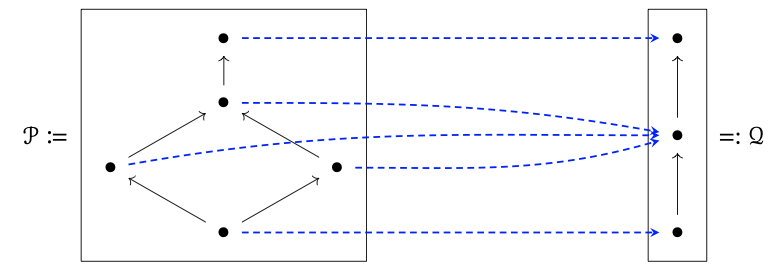
$Screen Shot 2021-01-17 en 2.53.48 PM.png$

Esto se parece a las fotos de puentes que conectan ciudades, y si uno considera la imagen de arriba en esa luz, están viendo al compañero$\widehat{F}$. Pero ahora mentalmente revertir cada flecha punteada, y el resultado serían puentes Q a P. Esto es un profuso Q → P! Nosotros lo llamamos$\breve{F}$.

Ejemplo 4.35.

Para cualquier preorden P, hay un functor de identidad id: P → P. Su compañero y conjunto acuerdan$\widehat{id}$ =$\breve{id}$: P → P. El profunctor resultante es de hecho el profunctor de unidad, U$_{P}$, como se define en la Ec. (4.25).

Ejemplo 4.36.

Comprueba que el compañero$\widehat{id}$ de id: P → P realmente tenga la fórmula del profunctor de la unidad dada en la Ec. (4.25) . ♦

Ejemplo 4.37.

Considera la función +:$\mathbb{R}$$\mathbb{R}$ × ×$\mathbb{R}$ →$\mathbb{R}$, enviando un triple (a, b, c) de números reales a a + b + $\in$$\mathbb{R}$c.

Esta función es monótona, porque si (a, b, c) ≤ (a ′, b ′, c ′) —es decir, si a ≤ a y b ≤ b, y c ≤ c entonces obviamente a + b + c ≤ a + b + c. Así tiene un compañero y un conjunto.

Su compañero$\widehat{+}$: ($\mathbb{R}$×$\mathbb{R}$ ×$\mathbb{R}$) →$\mathbb{R}$ es la función que envía (a, b, c, d) a true si a + b + c ≤ d y a false en caso contrario.

Ejercicio 4.38.

Dejar +:$\mathbb{R}$ ×$\mathbb{R}$ ×$\mathbb{R}$ →$\mathbb{R}$ ser como en el Ejemplo 4.37. ¿Cuál es su conjunto$\breve{+}$? ♦

OBSERVACIÓN 4.39 (V-Adjoint). Recordemos de la Definición 1.95 la definición de connec- ción de Galois entre preordenes P y Q. La definición de adjunto puede extenderse desde el entorno enriquecido en Bool (de preordenes y mapas monótonos) hasta el ajuste enriquecido en V para preordenes monoidales arbitrarios V. En ese caso, la definición de una V -adjunction es un par de funtores V F: P → Q y G: Q → P tal que se mantiene lo siguiente para todos los p$\in$ P y q$\in$ Q.

P (p, G (q))$\cong$ Q (F (p), q) (4.40)

Ejercicio 4.41.

Que V sea una quantale esquelética, que P y Q sean categorías V, y que F: P → Q y G: Q → P sean funtores V.

Mostrar que F y G son uniones V (como en la Ec. (4.40)) si y solo si el compañero q del primero es igual al conjunto de este último:$\widehat{F}$ =$\breve{G}$.
Use esto para probar que$\widehat{id}$ =$\breve{id}$, como se indicó en el Ejemplo 4.35. ♦

Collage de un profunctor. Hemos estado dibujando profunctores como puentes que conectan ciudades. Uno puede tener una idea de que dado un profunctor V Φ: X → Y entre las categorías V X e Y, hemos convertido Φ en una especie de nueva categoría V que tiene X a la izquierda e Y a la derecha. Esto funciona para cualquier V y profunctor Φ, y se llama la construcción collage.

Definición: 4.42.

Que V sea una quantale, que X e Y sean categorías V, y que Φ: X → Y sea un profunctor V. El collage de Φ, denotado Col (Φ) es la categoría V definida de la siguiente manera:

(i) Ob (Col (Φ)) := Ob (X) Ob (Y);
(ii) Para cualquier a, b$\in$ Ob (Col (Φ)), defina Col (Φ) (a, b)$\in$ V como

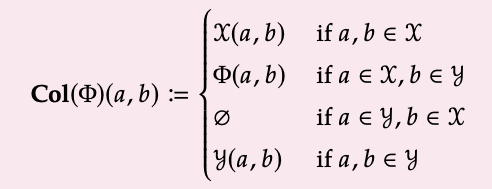
$Screen Shot 2021-01-17 a las 3.32.30 PM.png$

Hay funtores obvios$i_{x}$: X → Col (Φ) y$i_{y}$: Y → Col (Φ), enviando cada objeto y morfismo a “sí mismo”, llamadas inclusiones de collage.

Algunas imágenes ayudarán a aclarar esto.

Ejemplo 4.43.

Considere la siguiente imagen de un Profunctor de Costo Φ: X → Y:

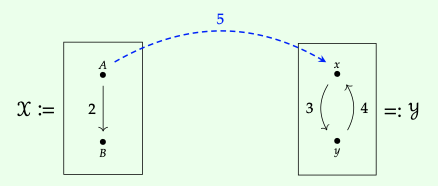
$Screen Shot 2021-01-17 a las 3.39.34 PM.png$

Corresponde a las siguientes matrices

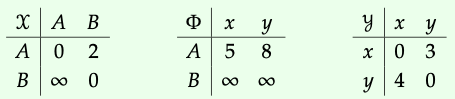
$Screen Shot 2021-01-17 a las 3.40.07 PM.png$

Se puede obtener un diagrama generalizado de Hasse del collage simplemente tomando la unión de los diagramas de Hasse para X e Y, y agregando los puentes como flechas. Dado el anterior Profunctor Φ, dibujamos el diagrama de Hasse para Col (Φ) abajo a la izquierda, y la representación Costo-matriz de la categoría Costo resultante a la derecha:

Ejercicio 4.44.

Dibuja un diagrama de Hasse para el collage del profunctor que se muestra aquí:

$Screen Shot 2021-01-17 a las 3.48.09 PM.png$