4.4: Categorización

Aquí cambiamos de marcha, para discutir un concepto general llamado categorización. Empezaremos de nuevo con lo básico, categorizando varias de las nociones que ya nos hemos encontrado. El objetivo es definir categorías cerradas compactas y sus diagramas de cableado estilo retroalimentación. En ese punto volveremos a la historia del co-diseño, y los profunctores V en general, y demostraremos que de hecho forman una categoría compacta cerrada, y así interpretar los diagramas que hemos estado dibujando desde la Ec. (4.1).

La idea básica de la categorización

La idea general de la categorización es que tomamos algo que conocemos y le agregamos estructura, para que lo que antes eran propiedades se conviertan en estructuras. Esto lo hacemos de tal manera que podemos recuperar lo que categorizamos olvidando esta nueva estructura. Esto es bastante vago; vamos a dar un ejemplo. La aritmética básica se refiere a las propiedades de los números naturales N, como el hecho de que 5 + 3 = 8. Una forma de categorizar N es usar la categoría FinSet de conjuntos finitos y funciones. Para obtener una categorización, reemplazamos los brutos 5, 3 y 8 con conjuntos de tantos elementos, digamos\(\underline{5}\) = {manzana, plátano, cereza, libélula, elefante},\(\underline{3}\) = {manzana, tomate, melón}, y\(\underline{8}\) = {Ali, Bob, Carl, Deb, Eli, Fritz, Gem, Helen} respectivamente. También reemplazamos + con unión disjunta de conjuntos, y la propiedad bruta de igualdad con la estructura de un isomorfismo. Lo que hace de esto una buena categorización es que, habiendo hecho estos reemplazos, el análogo de 5 + 3 = 8 sigue siendo cierto\(\underline{5}\):\(\underline{3}\)\(\cong\)\(\underline{8}\).

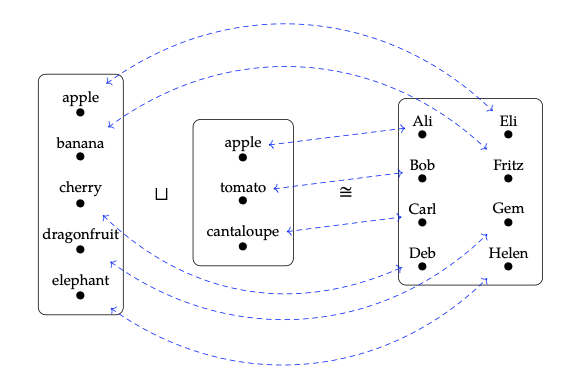
En este mundo categorizado, tenemos más estructura disponible para hablar de la relación- naves entre los objetos, así podemos ser más precisos sobre cómo se relacionan entre sí. Por lo tanto, no\(\underline{3}\) es el caso de que\(\underline{5}\) sea igual a nuestro conjunto de ocho elementos elegido 8, sino más precisamente que existe una función invertible comparando los dos, mostrando que son isomórficos en la categoría FinSet.

Tenga en cuenta que en la construcción anterior hicimos una serie de elecciones; aquí debemos tener cuidado. Elegir una buena categorización, como diseñar una buena estructura algebraica como la de preordenes o cuánticas, es parte del arte de las matemáticas. No hay una forma prescrita de categorizar, y el éxito de una categorización elegida suele ser empírico: su estructura más rica debería permitirnos una mayor comprensión del tema que queremos modelar.

Como otro ejemplo, una forma empíricamente agradable de categorizar los preordenes es cat- egorificarlos como, bien, categorías. En este caso, más que la propiedad bruta “existe un morfismo a → b”, denotado a ≤ b o P (a, b) = verdadero, en cambio decimos “aquí hay un conjunto de morfismos a → b”. Obtenemos un hom-set en lugar de un hom-booleano. De hecho, para afirmar esto de una manera directamente del ooze primordial, así como los pedidos anticipados son categorías Bool, las categorías ordinarias son en realidad Categorías Set.

reflexión sobre diagramas de cableado

Supongamos que tenemos una preorden. Introdujimos un tipo de diagrama de cableado muy simple en la Sección 2.2.2. Estos nos permitieron dibujar una caja

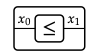
siempre que x\(_{0}\) ≤ x\(_{1}\). Encadanándolos juntos, podríamos probar hechos en nuestro preorden. Por ejemplo

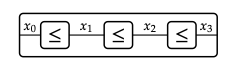
proporciona una prueba de que x\(_{0}\) ≤ x\(_{3}\) (la caja exterior) usando tres hechos (las cajas interiores), x\(_{0}\) ≤ x\(_{1}\)\(_{2}\), x\(_{1}\) ≤ x y x\(_{2}\) ≤ x \(_{3}\).

Como pedidos anticipados categorizados, las categorías tienen básicamente el mismo tipo de diagrama de cableado que los pedidos anticipados, es decir, secuencias de cajas dentro de una caja. Pero como hemos reemplazado el hecho de que x\(_{0}\) ≤ x\(_{1}\) por la estructura de un conjunto de morfismos, necesitamos poder etiquetar nuestras cajas con nombres de morfismo:

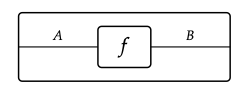
Supongamos dados morfismos adicionales g: B → C, y h: C → D. Representando estas cada una como cajas como hicimos para f, podríamos tener la tentación de pegarlas juntas para formar una nueva caja:

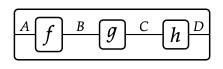
Idealmente esto también sería un morfismo en nuestra categoría: después de todo, hemos dicho que podemos representar morfismos con cajas con una entrada y una salida. ¡Pero espera, dices! No sabemos qué morfismo es. ¿Es f; (g; h)? O (f; g); h? Es bueno que seas tan cuidadoso. Por suerte, estamos salvados por las propiedades que debe tener una categoría.

La asociatividad dice f; (g; h) = (f; g); h, así que no importa de qué manera elegimos intentar decodificar la caja.

De igual manera, el morfismo de identidad sobre un objeto x se dibuja como a la izquierda de abajo, pero veremos que no es dañino dibujar id\(_{x}\) de ninguna de las siguientes tres formas:

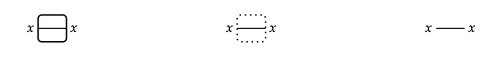
Por Definición 3.6 los morfismos en una categoría satisfacen dos propiedades, denominadas propiedad de unidad y propiedad de asociatividad.

La unidad dice que id\(_{x}\); f = f = f = id\(_{y}\) para cualquier f: x → y. En cuanto a diagramas esto diría

Esto significa que puedes insertar o descartar cualquier morfismo de identidad que veas en un diagrama de cableado. Desde esta perspectiva, las leyes de coherencia de una categoría es decir, la ley de asociatividad y la ley de unidad son precisamente lo que se necesita para asegurar que podamos alargar y acortar cables sin ambigüedades.

En la Sección 2.2.2, también vimos diagramas de cableado para preordenes monoidales. Aquí se nos permitió dibujar cajas que pueden tener múltiples entradas y salidas mecanografiadas, pero sin elección de etiqueta (siempre ≤):

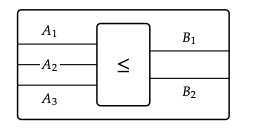
Si combinamos estas ideas, obtendremos una categorización de preordenes monoidales simétricos: categorías monoidales simétricas. Una categoría monoidal simétrica es una estructura algebraica en la que hemos etiquetado cajas con múltiples entradas y salidas mecanografiadas:

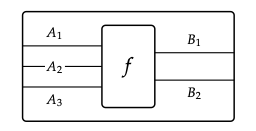
Además, una categoría monoidal simétrica tiene una regla de composición y un producto monoidal, lo que nos permite combinar estas cajas para interpretar diagramas como este:

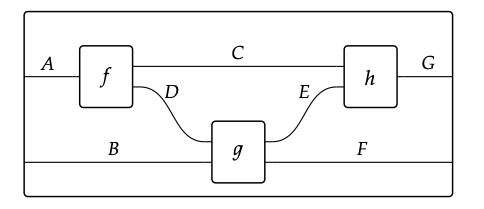
Por último, esta estructura debe obedecer leyes de coherencia, análogas a la asociatividad y a la unidad en categorías, que permitan interpretar dichos diagramas de manera inequívoca. En la siguiente sección seremos un poco más formales, pero es útil tener presente que, cuando decimos que nuestros datos deben estar “bien portados”, esto es lo único que queremos decir.

Categorías monoidales

Definimos categorías V, para un preorden monoidal simétrico V en la Definición 2.46. Al igual que los pedidos anticipados resultaron ser tipos especiales de categorías (ver Sección 3.2.3), los preordenes monoidales son tipos especiales de categorías monoidales. Y así como podemos considerar categorías V para un preorden monoidal, también podemos considerar categorías V cuando V es una categoría monoidal. Este es otro tipo de categorización.

Pronto conoceremos la categoría monoidal (Set, {1}, ×). El producto monoidal tomará dos juegos, S y T, y devolverá el conjunto S × T = {(s, t) | s\(\in\) S, t\(\in\) T}. Pero mientras que para los preordenes monoidales teníamos la propiedad asociativa bruta (p q) r = p (q r), la idea correspondiente en Set no es del todo cierta:

\ (\ comenzar {alineado}
& S\ veces (T\ veces U) :=\ {(s, (t, u))\ mediados s\ en S, t\ en T, u\ en U\}\\
=? & (S\ veces T)\ veces U: =\ {((s, t), u)\ mediados s\ en S, t\ en T, u\ en U\}
\ final {alineado}\)

Son conjuntos ligeramente diferentes: el primero contiene pares que consisten en un elemento en S y un elemento en T × U, mientras que el segundo contiene pares que consisten en un elemento en S × T y un elemento en U. Los conjuntos no son iguales, pero son claramente isomórficos, es decir, la diferencia entre ellos es “solo cuestión de contabilidad”. Por lo tanto, necesitamos una estructura un isomorfismo contable para hacer un seguimiento de la asociatividad:

\(\alpha_{s, t, u}:\{(s,(t, u)) \mid s \in S, t \in T, u \in U\} \stackrel{\cong}{\rightarrow}\{((s, t), u) \mid s \in S, t \in T, u \in U\}\)

Hay un par de cosas que mencionar antes de sumergirnos en estas ideas. Primero, solo porque reemplaces cosas y propiedades brutas por estructuras, no significa que ya no tengas cosas y propiedades brutas: ¡emergen otras nuevas! No sólo eso, sino segundo, las nuevas cosas brutas tienden a ser más complejas de lo que empezaste con. Por ejemplo, arriba reemplazamos la ecuación de asociatividad por un isomorfismo α s, t, u, ¡pero ahora necesitamos una propiedad más compleja para asegurar que todos estos α se comporten razonablemente! La única manera de salir de este pantano es agregar infinitamente mucha estructura, lo que lleva a uno a “∞ -categorías”, pero no vamos a discutir eso aquí.

En cambio, continuaremos con nuestra categorización de preordenes monoidales, comenzando con una definición aproximada de categorías monoidales simétricas. Es rudo en el sentido de que suprimimos la contabilidad técnica, ocultándola bajo el nombre de “bien portado”.

Definición aproximada: 4.45.

Que C sea una categoría. Una estructura monoidal simétrica en C consta de los siguientes constituyentes:

(i) un objeto I\(\in\) Ob (C) llamado unidad monoidal, y

(ii) un funtor: C × C → C, llamado el producto monoidal

sujeto a isomorfismos naturales de buen comportamiento

(a) λ\(_{c}\): I c \(\cong\)c por cada c\(\in\) Ob (C),

b) ρ\(_{c}\): c I\(\cong\) c por cada c\(\in\) Ob (C),

(c) α\(_{c,d,e}\) :( c d) e\(\cong\) c (d e) por cada c, d, e\(\in\) Ob (C), y

(d) σ\(_{c,d}\): c d \(\cong\)d c por cada c, d\(\in\) Ob (C), llamado mapa de swap, de tal manera que σ ◦ σ = id.

Una categoría equipada con una estructura monoidal simétrica se denomina categoría monoidal simétrica.

Obración 4.46. Si los isomorfismos en (a), (b) y (c) —pero no (d) —son reemplazados por igualdades, entonces decimos que la estructura monoidal es estricta, y esta es una definición completa (no aproximada) de categoría monoidal estricta simétrica. De hecho, las categorías monoidales estrictas simétricas son casi lo mismo que las categorías monoidales simétricas, a través de un resultado conocido como teorema de coherencia de Mac Lane. Un resultado de este teorema es que podemos, cuando nos sea útil, pretender que nuestras categorías monoidales son estrictas: por ejemplo, lo hacemos implícitamente cuando dibujamos diagramas de cableado. ¡Pide a tu amable teórico de la categoría de barrio que te explique cómo!

Obración 4.47. Para aquellos que aún no han encontrado un experto amigable teórico de la categoría, hacemos el siguiente comentario. Una definición completa (no aproximada) de categoría monoidal simétrica es que una categoría monoidal simétrica es una categoría equipada con una equivalencia a (la categoría subyacente de) una categoría monoidal estricta simétrica. Esto se puede desempaquetar, usando Observación 4.46 y nuestro comentario sobre equivalencia de categorías en Observación 3.59, pero no esperamos que lo haga. En cambio, ¡esperamos que esto te dé más incentivo para preguntarle a un amable teórico de categoría experto!

Ejercicio 4.48.

Comprobar que las categorías monoidales de hecho generalizan preordenes monoidales: un preorden monoidal es una categoría monoidal (P, I,) donde,

por cada p, q\(\in\) P, el conjunto P (p, q) tiene como máximo un elemento. ♦

Ejemplo 4.49.

Como dijimos anteriormente, hay una estructura monoidal en Set donde la unidad monoidal es alguna elección de conjunto singleton, digamos I := {1}, y el producto monoidal es: = ×. Lo que significa que × es un functor es que:

• Para cualquier par de objetos, es decir, conjuntos, (S, T)\(\in\) Ob (Set × Set), se obtiene un conjunto (S × T)\(\in\) Ob (Set). Sabemos lo que es: el conjunto de pares {(s, t) | s\(\in\) S, t\(\in\) T}.
• Para cualquier par de morfismos, es decir funciones, f: S → S ′ y g: T → T ′, se obtiene una función (f × g): (S × T) → (S ′× T ′). Funciona puntualmente: (f × g) (s, t) := (f (s), g (t)).
• Estos deben preservar las identidades: id\(_{S}\) × id\(_{T}\) = id\(_{S×T}\) para cualquier conjunto S, T.
• Estos deben preservar la composición: para cualquier función\(S \stackrel{f}{\rightarrow} S^{\prime} \stackrel{f^{\prime}}{\rightarrow} S^{\prime \prime} \text { and } T \stackrel{g}{\rightarrow} T^{\prime} \stackrel{g^{\prime}}{\rightarrow} T^{\prime \prime}\), uno tiene

(f × g); (f '× g') = (f; g) × (f'; g').

Las cuatro condiciones, (a), (b), (c) y (d) dan isomorfismos {1} × \(\cong\)S S, etc.

Estos mapas son obvios en el caso de Set, por ejemplo la función {(1, s) | \(\in\)s S} → S enviando (1, s) a s. Hemos estado llamando a tales cosas teneduría de libros.

Ejercicio 4.50.

Considera la categoría monoidal (Set, 1, ×), junto con el diagrama

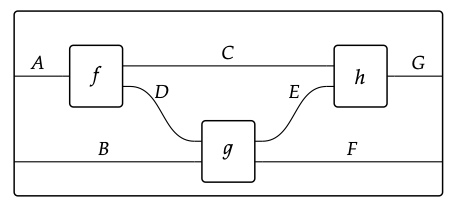
Supongamos que A = B = C = D = F = G = Z y E\(\mathbb{B}\) = = {verdadero, falso}, y supongamos que f\(_{C}\) (a) = | a |, f\(_{D}\) (a) = a ∗ 5, g\(_{E}\) (d, b) = “d ≤ b”, g\(_{F}\) (d, b) = d − b, y h (c, e) = si e entonces c else 1 − c.

1. ¿Qué son g\(_{E}\) (5,3) y g\(_{F}\) (5,3)?

2. ¿Qué son g\(_{E}\) (3,5) y g\(_{F}\) (3,5)?

3. ¿Qué es h (5, true)?

4. ¿Qué es h (−5, true)?

5. ¿Qué es h (−5, false)?

Todo el diagrama define ahora una función A × B → G × F; llámala q.

6. ¿Qué son q\(_{G}\) (−2, 3) y q\(_{F}\) (−2, 3)?

7. ¿Qué son q\(_{G}\) (2, 3) y q\(_{F}\) (2, 3)?

Veremos más categorías monoidales a lo largo del resto de este libro. ♦

Categorías enriquecidas en una categoría monoidal simétrica

No volveremos a necesitar esto, pero alguna vez nos comprometimos a explicar por qué las categorías V, donde V es un preorden monoidal simétrico, merecen ser vistas como tipos de categorías. La razón, como hemos insinuado, es que las categorías deberían llamarse realmente Set -categories. Pero espera, ¡Set no es un preorder! Tendremos que generalizar—categorizar—V-categorías.

Ahora damos una definición aproximada de categorías enriquecidas en una categoría monoidal simétrica V. Al igual que en la Definición 4.45, suprimimos algunas partes técnicas en este boceto, ocultándolas bajo el nombre de “leyes asociativas y unitales habituales”.

Definición aproximada: 4.51.

Que V sea una categoría monoidal simétrica, como en la Definición 4.45. Para especificar una categoría enriquecida en V, o una categoría V, denotada X,

i) se especifica una colección Ob (X), cuyos elementos se denominan objetos;

(ii) para cada par x, y\(\in\) Ob (X), se especifica un objeto X (x, y)\(\in\) V, llamado hom-object para x, y;

iii) por cada x\(\in\) Ob (X), se especifica un id de morfismo\(_{x}\): I → X (x, x) en V, denominado elemento de identidad;

(iv) por cada x, y, z\(\in\) Ob (X), se especifica un morfismo;: X (x, y) X (y, z) → X (x, z), denominado morfismo de composición.

Estos constituyentes están obligados a satisfacer las leyes asociativas y unitarias habituales.

La definición precisa, no aproximada, se puede encontrar en otras fuentes, por ejemplo [nLa18], [Wik18], [Kel05].

Ejercicio 4.52.

Recordemos del Ejemplo 4.49 que V = (Set, {1}, ×) es una categoría monoidal simétrica. Esto significa que podemos aplicar la Definición 4.51. ¿La definición (aproximada) concuerda aproximadamente con la definición de categoría dada en la Definición 3.6? ¿O hay una diferencia sutil? ♦

Obración 4.53. Primero definimos las categorías V en la Definición 2.46, donde se requería que V fuera un preorden monoidal. Para verificar que no estamos abusando de nuestros términos, es una buena idea asegurarse de que las categorías V según la Definición 2.46 siguen siendo categorías V según la Definición 4.51.

Lo primero que hay que observar es que cada preorden monoidal simétrico es una categoría monoidal simétrica (Ejercicio 4.48). Entonces dado un preorden monoidal simétrico V, podemos aplicar la Definición 4.51. Los datos requeridos (i) y (ii) luego nos llevan a un buen comienzo: ambas definiciones de categoría V requieren objetos y hom-objects, y se especifican de la misma manera. Por otra parte, la Definición 4.51 requiere de dos datos adicionales: (iii) elementos de identidad y (iv) morfismos de composición. ¿De dónde vienen estos?

En el caso de los pedidos anticipados, existe a lo sumo un morfismo entre dos objetos cualesquiera, por lo que no necesitamos elegir un elemento de identidad y un morfismo de composición. En cambio, solo tenemos que asegurarnos de que exista un elemento de identidad y un morfismo de composición. Esto es exactamente lo que dicen las propiedades (a) y (b) de la Definición 2.46.

Por ejemplo, el requisito (iii) de que una categoría V X tenga un elemento de identidad elegido id x: I → X (x, x) para el objeto x simplemente se convierte en el requisito (a) de que I ≤ X (x, x) es verdadero en V. Esto es típico de la historia de la categorización: lo que eran meras propiedades en la Definición 2.46 se han convertido en estructuras en la Definición 4.51.

Ejercicio 4.54.

¿Qué son los elementos de identidad en los espacios métricos de Lawvere (es decir, Cost -categories)? ¿Cómo interpretamos esto en términos de distancias? ♦