4.5: Profunctores forman una Categoría Cerrada Compacta
- Page ID
- 112138
En esta sección definiremos categorías cerradas compactas y mostraremos que los Feas, y más generalmente los profunctores V, forman tal cosa. Las categorías compacto-cerradas son categorías monoidales cuyos diagramas de cableado permiten retroalimentación. Los diagramas de cableado se ven así:
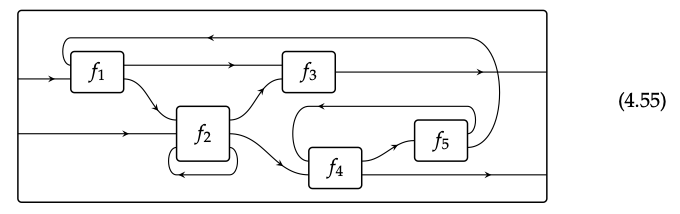
Ha pasado un tiempo desde que pensamos en el codiseño, pero estos fueron los tipos de diagramas de cableado que dibujamos, por ejemplo, conectar el chasis, el motor y la batería en la Ec. (4.1). Las categorías cerradas compactas son categorías monoidales simétricas, con un poco más de estructura que nos permiten interpretar formalmente los tipos de retroalimentación que ocurren en los problemas de co-diseño. Esta misma estructura se manifiesta en muchos otros campos, incluyendo la mecánica cuántica y los sistemas dinámicos.
En la Ec. (2.13) y Sección 2.2.3 discutimos varios tipos de diagramas de cableado, incluyendo aquellos con iconos para dividir y terminar cables. Para las categorías compacto-cerradas, nuestros iconos adicionales nos permiten doblar las salidas en entradas, y viceversa. Para hacer un seguimiento de esto, sin embargo, dibujamos flechas en nuestro cable, que pueden apuntar hacia adelante o hacia atrás. Por ejemplo, podemos dibujar esto

Luego agregamos iconos, llamados tapa y copa, permitiendo que cualquier cable invierta la dirección de adelante hacia atrás y de atrás hacia adelante.
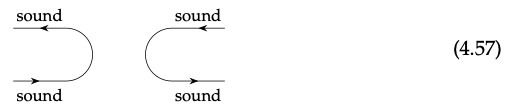
Así podemos dibujar lo siguiente (4.57)
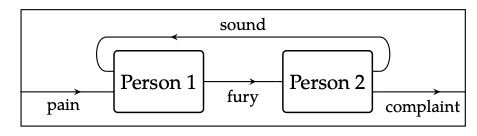
y su significado es equivalente al de la Ec. (4.56).
Comenzaremos dando los axiomas para una categoría cerrada compacta. Luego volveremos a analizar las relaciones de factibilidad en el codiseño y, más generalmente, a los prospectores enriquecidos, y mostraremos que de hecho forman una categoría cerrada compacta.
Categorías compactas cerradas
Como dijimos, las categorías cerradas compactas son categorías monoidales simétricas (ver Definición 4.45) con estructura extra.
Sea (C, I,) una categoría monoidal simétrica, y c\(\in\) Ob (C) un objeto. Un doble para c consta de tres componentes
i) un objeto c ∗\(\in\) Ob (C), denominado el dual de c,
ii) un morfismo η\(_{c}\): I → c ∗ c, denominado la unidad para c,
(iii) un morfismo ε\(_{c}\): c c ∗ → I, llamado el counit para c
Estos son necesarios para satisfacer dos ecuaciones por cada c\(\in\) Ob (C), que dibujamos como diagramas conmutativos:
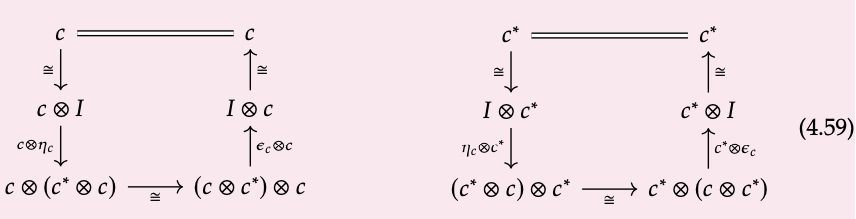
Estas ecuaciones a veces se llaman las ecuaciones de serpiente.
Si por cada objeto c\(\in\) Ob (C) existe un doble c ∗ para c, entonces decimos que (C, I,) es compacto cerrado.
En una categoría cerrada compacta, cada cable está equipado con una dirección. Para cualquier objeto c, un cable que apunta hacia adelante etiquetado como c se considera equivalente a un
escribir etiquetado c*, es decir\(\stackrel{c}{\rightarrow} \text { is the same as } \stackrel{c^{*}}{\leftarrow} \text { . }\) La copa y la tapa discutidos anteriormente son de hecho los morfismos de unidad y cuenta; se dibujan de la siguiente manera.

En los diagramas de cableado, las ecuaciones de serpiente (4.59) se dibujan de la siguiente manera:
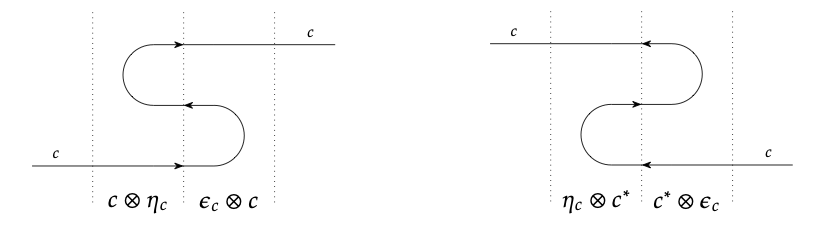
Tenga en cuenta que las imágenes en la Ec. (4.57) corresponden a ε\(_{sound}\) y η\(_{sound∗}\).
Recordemos la noción de preorden cerrado monoidal; una categoría monoidal también puede ser cerrada monoidal. Esto significa que por cada par de objetos c, d\(\in\) Ob (C) hay un objeto c -o d y un isomorfismo C (b c, d)\(\cong\) C (b, c -o d), natural en b. Si bien no proporcionaremos una prueba completa aquí, las categorías cerradas compactas se denominan así porque son un tipo especial de categoría cerrada monoidal.
Si C es una categoría compacta cerrada, entonces
1. C es monoidal cerrado; y para cualquier objeto c\(\in\) Ob (C),
2. si c ∗ y c′ son ambos duales a c entonces hay un isomorfismo \(^{∗}\)\(\cong\)c c'; y
3. hay un isomorfismo entre c y su doble-dual, \(\cong\)\(^{∗∗}\)c.
Para probar 1., la idea clave es que para cualquier c y d, el objeto c -o d viene dado por c ∗ d, y el isomorfismo natural C (b c, d)\(\cong\) C (b, c - o d) se da precomponiendo con\(_{b}\) id η\(_{c}\).
Antes de volver al codiseño, damos otro ejemplo de una categoría compacta cerrada, llamada Corel, que volveremos a ver en los capítulos por venir.
Recordemos, de la Definición 1.18, que una relación de equivalencia en un conjunto A es una relación binaria reflexiva, simétrica y transitiva sobre A. Dados dos conjuntos finitos, A y B, una corelación A → B es una relación de equivalencia sobre A B.
Entonces, por ejemplo, aquí hay una corelación de un conjunto A que tiene cinco elementos a un conjunto B que tiene seis elementos; dos elementos son equivalentes si están rodeados por la misma línea discontinua.
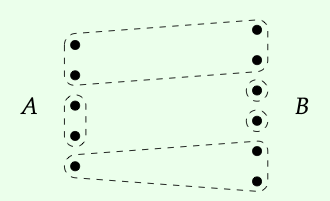
Existe una categoría, denotada Corel, donde los objetos son conjuntos finitos, y donde un morfismo de A → B es una corelación A → B. La regla de composición es más sencilla de mirar que escribir formalmente. \(^{2}\)Si además de la corelación α: A → B anterior tenemos otra corelación β: B → C
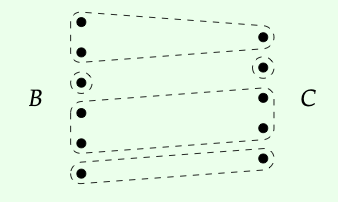
Entonces el compuesto β ◦ α de nuestras dos corelaciones viene dado por
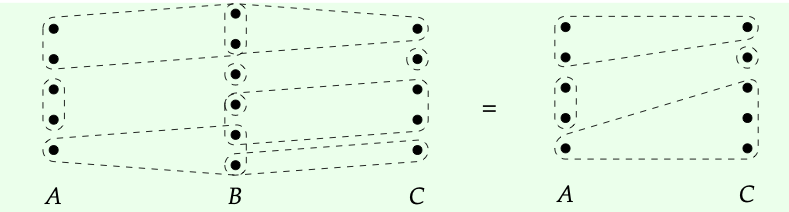
Es decir, dos elementos son equivalentes en la corelación compuesta si podemos viajar de uno a otro permaneciendo dentro de las clases de equivalencia de α o β.
La categoría Corel puede estar equipada con la estructura monoidal simétrica (Ø,). Esta categoría monoidal es compacta cerrada, con cada conjunto finito su propio dual. En efecto, tenga en cuenta que para cualquier conjunto finito A hay una relación de equivalencia en A A: = {(a, 1), (a, 2) | a \(\in\)A} donde cada parte consiste simplemente en los dos elementos (a, 1) y ( a ,2) para cada una\(\in\) A. La unidad en un conjunto finito A es la corelación η:Ø\(_{A}\) → A A especificada por esta relación de equivalencia; de manera similar el counit en A es la corelación ε:\(_{A}\) A A → Ø especificada por esta misma relación de equivalencia.
Ejercicio 4.62.
Considera el conjunto\(\underline{3}\) = {1, 2, 3}.
1. Dibuja una imagen de la corelación de unidad Ø → 3 3.
2. Dibuja una imagen de la corelación counit 3 3 → Ø.
3. Verifique que las ecuaciones de serpiente (4.59) se mantengan. (Dado que cada objeto es su propio dual, solo necesitas verificar uno de ellos. ) ♦
Feas como categoría cerrada compacta
Cerramos el capítulo volviendo al co-diseño y mostrando que Feas tiene una estructura cerrada compacta. Esto es lo que nos permite dibujar los tipos de diagramas de cableado que vimos en las ecuaciones (4.1), (4.55) y (4.56): es lo que pone las matemáticas reales detrás de estas imágenes.
En lugar de simplemente detallar esta estructura cerrada compacta para Feas = Prof\(_{Bool}\), no es un trabajo extra demostrar que para cualquier quantale esquelético (unital, conmutativo) (V, I,) la categoría profunctor Prof\(_{V}\) of Theorema 4.23 es compacta cerrada, así que vamos discutir este hecho general.
Que V sea una quantale esquelética. A la categoría Prof se le\(_{V}\) puede dar la estructura de una categoría cerrada compacta, con producto monoidal dado por el producto de categorías V.
En efecto, todo lo que tenemos que hacer es construir la estructura monoidal y los duales para los objetos. Vamos a bosquejar cómo va esto.
Los productos monoidales en Prof\(_{V}\) son solo categorías de productos. En cuanto a los diagramas de cableado, la estructura monoidal parece apilar cables o cajas uno encima del otro, sin nueva interacción.
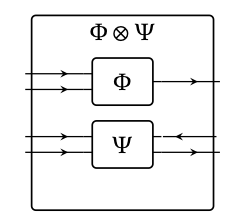
Tomamos nuestro producto monoidal sobre el Prof V como el que da el producto de las categorías V; la definición se dio en la Definición 2.74, y ahí elaboramos varios ejemplos. Para recordar, la fórmula para los hom-sets en X × Y viene dada por
\((x \times y)\left((x, y),\left(x^{\prime}, y^{\prime}\right)\right):=X\left(x, x^{\prime}\right) \otimes y\left(y, y^{\prime}\right)\)
Pero también hay que dar productos monoidales sobre los morfismos, y los morfismos en el Prof\(_{V}\) son profunctores V. Entonces dados los profunctores V Φ: X1 → X2 y ψ: Y1 → Y2, uno define un Profunctor V (Φ × ψ): X1 × Y1 → X2 × Y2 por
\((\Phi \times \Psi)\left(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right):=\Phi\left(x_{1}, x_{2}\right) \otimes \Psi\left(y_{1}, y_{2}\right)\).
Ejercicio 4.64.
Interpretar los productos monoidales en Prof\(_{Bool}\) en términos de factibilidad. Es decir, los pedidos por adelantado representan recursos ordenados por disponibilidad (x ≤ x ′ significa que x está disponible dado x ′) y un profunctor es una relación de factibilidad. Explique por qué X × Y tiene sentido como producto monoidal de los preordenes de recursos X e Y y por qué Φ × ψ tiene sentido como producto monoidal de las relaciones de factibilidad Φ y ψ. ♦
La unidad monoidal en el Prof\(_{V}\) es 1. Para definir una estructura monoidal sobre el Prof\(_{V}\), necesitamos no solo un producto monoidal, como se definió anteriormente, sino también una unidad monoidal. Recordemos la categoría V 1; tiene un objeto, digamos 1, y (1, 1) = I es la unidad monoidal de V. Tomamos 1 para ser la unidad monoidal del Prof\(_{V}\).
Ejercicio 4.65.
Para que 1 sea una unidad monoidal, se supone que hay isomor-fismos X × 1 → X y 1 × X → X en Prof\(_{V}\), para cualquier V-categoría X. ¿Qué son? ♦
Los duales en Prof\(_{V}\) son categorías justo opuestas. Para considerar al Prof\(_{V}\) como una categoría cerrada compacta (Definición 4.58), queda por especificar los duales y la copa y tapa correspondientes.
Los duales son fáciles: por cada categoría V X, su dual es su categoría X opuesta\(^{op}\) (ver Ejercicio 2.73). La unidad y el counit lucen entonces como identidades. Para elaborar, la unidad es un Profunctor V\(_{ηX}\) → 1 X\(^{op}\) × X. Por definición, este es un V-functor
\(\eta_{x}: \mathbf{1} \times x^{\mathrm{op}} \times x \rightarrow v\);
lo definimos por\(_{ηX}\) (1, x, x ′) := X (x, x ′). De igual manera, el counit es el profunctor ε\(_{X}\): (X × X\(^{op}\)) → 1, definido por ε\(_{X}\) (x, x ′, 1) := X (x, x ′).
Ejercicio 4.66.
Verifica estas unidades propuestas y los cómputos efectivamente obedecen las ecuaciones de serpiente Eq. (4.59) . ♦


