5.3: Gráficos de flujo de señal simplificados
- Page ID
- 112182
Ahora volvemos a los gráficos de flujo de señal, expresándolos en términos de apoyos. Discutiremos una forma simplificada sin retroalimentación (el único tipo que hemos discutido hasta ahora), y luego extenderemos a la forma habitual de gráficos de flujo de señal en la Sección 5.4.3. Pero antes de que podamos hacer eso, debemos decir lo que queremos decir con señales; esto nos mete en la estructura algebraica de “plataformas”. Llegaremos a señalar gráficas de flujo en la Sección 5.3.2.
Rigs
Las señales se pueden amplificar y se pueden agregar. La adición y la amplificación interactúan a través de una ley distributiva, de la siguiente manera: si agregamos dos señales, y luego las amplificamos en alguna cantidad a, debería ser lo mismo que amplificar las dos señales por separado por a, luego agregar los resultados.
Podemos pensar en todas las amplificaciones posibles como formar una estructura llamada rig,7 definida de la siguiente manera.
Una plataforma es una tupla (R, 0, +, 1, ∗), donde R es un conjunto, 0, 1\(\in\) R son elementos, y +, ∗: R × R → R son funciones, tal que
- (R, +, 0) es un monoide conmutativo,
- (R, ∗, 1) es un monoide,\(^{8}\) y
- a ∗ (b + c) = a ∗ b + a ∗ c y (a + b) ∗ c = a ∗ c + b ∗ c para todos a, b , c\(\in\) R.
- a ∗ 0 = 0 = 0 ∗ a para todos a\(\in\) R.
Ya nos hemos encontrado con muchos ejemplos de plataformas.
Los números naturales forman una plataforma (\(\mathbb{N}\), 0, +, 1, ∗).
Los booleanos forman una plataforma (\(\mathbb{B}\), falso,\(\bigvee\), verdadero,\(\bigwedge\)).
Cualquier cuantale V = (V, ≤, I,) determina un rig (V, 0,\(\bigvee\), I,), donde 0 =\(\bigvee\) Ø es la unión vacía. Ver Definición 2.79.
Si R es una plataforma y n\(\in\) N es cualquier número natural, entonces el conjunto Mat\(_{n}\) (R) de matrices (n × n) en R forma una plataforma. Una matriz M\(\in\) M a n (R) es una función M:\(\underline{n}\) ×\(\underline{n}\) → R.
La adición M + N de matrices viene dada por (M + N) (i, j) := M (i, j) + N (i, j) y multiplicación M∗ N viene dado por (M ∗ N) (i, j) :=\(\Sigma\)\(_{k \in \underline{n}}\) M (i, k) ∗ N (k, j). La matriz 0 es 0 (i, j) := 0 para todos i, j\(\in\)\(\underline{n}\). Tenga en cuenta que Mat\(_{n}\) (R) generalmente no es conmutativo.
1. Dijimos en el Ejemplo 5.40 que para cualquier plataforma R, el conjunto Mat\(_{n}\) (R) forma una plataforma. ¿Cuál es su identidad multiplicativa 1\(\in\) Mat\(_{n}\) (R)?
2. También dijimos que Mat\(_{n}\) (R) generalmente no es conmutativo. Escoge una n y muestra que ese Mat\(_{n}\) (\(\mathbb{N}\)) no es conmutativo, donde\(\mathbb{N}\) es como en el Ejemplo 5.37. ♦
Cualquier anillo forma una plataforma. En particular, los números reales (\(\mathbb{R}\), 0, +, 1, ∗) son una plataforma. La diferencia entre un anillo y una plataforma es que un anillo, además de todas las propiedades de una plataforma, también debe tener inversos aditivos, o negativos. Un mnemotécnico común es que una plataforma es un ri n g sin n egativos.
La iconografía de las gráficas de flujo de señal
Se supone que un gráfico de flujo de señal debe realizar un seguimiento de la amplificación, por elementos de una plataforma R, a la que se someten las señales. Si bien no es estrictamente necesario,\(^{9}\) asumiremos que las señales en sí mismas son elementos del mismo rig R. Nos referimos a los elementos de R como señales por el momento.
La amplificación de una señal por algún valor a\(\in\) R se representa simplemente así:

Interpretamos el icono anterior como una representación de un sistema donde una señal entra en el cable izquierdo, se multiplica por a, y se emite en el cable de la derecha.
Lo que es más interesante que una sola amplificación de señal, sin embargo, es la interacción de las señales. Hay otros cuatro iconos importantes en las gráficas de flujo de señal.
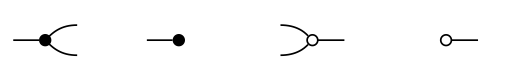
Vamos a repasarlos uno por uno. Los dos primeros son viejos amigos del Capítulo 2: copiar y desechar.

Interpretamos este diagrama como tomar una señal de entrada a la izquierda, y emitir ese mismo valor a ambos cables de la derecha. Se trata básicamente de la operación de “copia” de la Sección 2.2.3.
A continuación, tenemos la capacidad de descartar señales.

Esto toma cualquier señal, y no da salida a nada. Se trata básicamente de la operación de “residuos” de la Sección 2.2.3. A continuación, tenemos la capacidad de sumar señales.

Esto toma las dos señales de entrada y las agrega, para producir una única señal de salida. Por último, tenemos la señal cero.

Esto no tiene entradas, pero siempre da salida al elemento 0 de la plataforma.
Usando estos iconos, podemos construir gráficas de flujo de señal más complejas. Para calcular la operación realizada por un gráfico de flujo de señal simplemente trazamos los caminos con las interpretaciones anteriores, enchufando las salidas de un icono en las entradas del siguiente icono.
Por ejemplo, considere el rig R =\(\mathbb{N}\) del Ejemplo 5.37, donde los escalares son los números naturales. Recordemos el gráfico de flujo de señal de la Ec. (5.1) en la introducción:
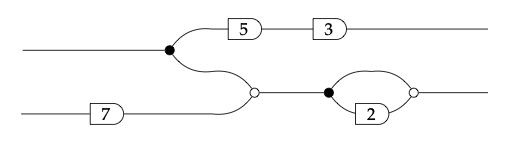
Como explicamos, esto toma dos señales de entrada x e y, y devuelve dos señales de salida a = 15 x y b = 3 x + 21 y.
Además de trazar el procesamiento de los valores a medida que avanzan a través de la gráfica, también podemos calcular estos valores sumando sobre rutas. Más explícitamente, para obtener la contribución de un cable de entrada dado a un cable de salida dado, tomamos la suma, sobre todos los caminos p que unen los cables, de la amplificación total a lo largo de esa ruta.
Entonces, por ejemplo, hay una ruta desde la entrada superior hasta la salida superior. En esta ruta, primero se copia la señal, lo que no afecta su valor, luego se amplifica en 5, y finalmente se amplifica por 3. Así, si x es la primera señal de entrada, entonces esto aporta 15 x a la primera salida. Dado que no hay ruta desde la entrada inferior hasta la salida superior (no se permite que una atraviese caminos hacia atrás), la señal en la primera salida es exactamente de 15 x. Ambas entradas contribuyen a la salida inferior. De hecho, cada entrada contribuye de dos maneras, ya que hay dos rutas hacia ella desde cada entrada. La entrada superior aporta así 3 x = x + 2 x, mientras que la entrada inferior, pasando por una amplificación adicional de *7, aporta 21 y.
El siguiente gráfico de flujo toma en dos números naturales x e y
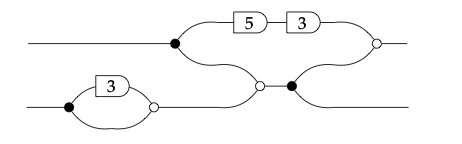
y produce dos señales de salida. ¿Qué son? ♦
Este ejemplo es para quienes tienen cierta familiaridad con las ecuaciones diferenciales. Un sistema lineal de ecuaciones diferenciales proporciona una manera sencilla de especificar el movimiento de una partícula. Por ejemplo, considere una partícula cuya posición (x, y, z) en el espacio tridimensional está determinada por las siguientes ecuaciones:
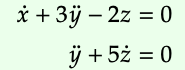
Usando lo que se conoce como la transformada de Laplace, se puede convertir esto en un sistema lineal que involucra una variable formal D, que significa “diferenciar”. Entonces el sistema se convierte
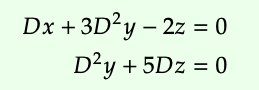
que puede ser representado por el gráfico de flujo de señal
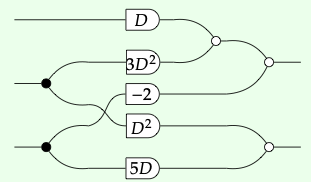
Gráficas de flujo de señal como morfismos en un prop libre. Podemos definir formalmente gráficos de flujo de señal simplificados usando props.
Que R sea una plataforma (ver Definición 5.36). Considera el conjunto

y vamos a, t: G\(_{R}\) →\(\mathbb{N}\) estar dados por el número de cables colgados a la izquierda y derecha del icono del generador respectivamente. Un gráfico de flujo de señal simplificado es un morfismo en el prop libre Libre (G\(_{R}\)) en este conjunto G\(_{R}\) de generadores. Definimos SFG\(_{R}\) := Libre (G\(_{R}\)).
Por ahora bajaremos el término 'simplificado', ya que estos son el único tipo de gráfico de flujo de señal que conocemos. Volveremos a los gráficos de flujo de señal en toda su gloría—es decir, incluyendo retroalimentación en la Sección 5.4.3.
Para estar más en línea con nuestras representaciones tanto de diagramas de cableado como de gráficos de puertos, los morfismos en Free (G\(_{R}\)) deben dibujarse de manera ligeramente diferente. Por ejemplo, técnicamente el gráfico de flujo de señal del Ejercicio 5.43 debe dibujarse de la siguiente manera:
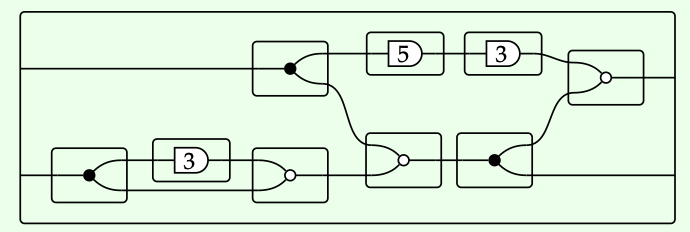
porque dijimos que etiquetaríamos cajas con los elementos de G. Pero es más fácil a la vista dibujar quitar las cajas y solo mirar los iconos dentro como en el Ejercicio 5.43, y así dibujaremos nuestros diagramas de esa manera.
Más importante aún, los apoyos proporcionan un lenguaje para comprender la semántica de los gráficos de flujo de señal. Aunque los propios gráficos de flujo de señal son apoyos libres, sus semánticas, su significado en nuestro modelo de flujo de señales, surgirán cuando agreguemos ecuaciones a nuestros apoyos, como en la Definición 5.33. Estas ecuaciones nos dirán cuándo dos gráficas de flujo de señal actúan de la misma manera sobre las señales. Por ejemplo,

ambos expresan el mismo comportamiento: una sola señal de entrada se copia dos veces para que se salgan tres copias idénticas de la señal de entrada.
Si dos gráficas de flujo de señal S, T son casi iguales, siendo la única excepción que en algún lugar reemplazamos el lado izquierdo de la ecuación (5.47) por el lado derecho, entonces S y T tienen el mismo comportamiento. Pero hay otros reemplazos que podríamos hacer a un gráfico de flujo de señal que no cambien su comportamiento. Nuestro siguiente objetivo es encontrar una descripción completa de estos reemplazos.
El puntal de matrices sobre una plataforma
Los gráficos de flujo de señal están estrechamente relacionados con las matrices. En capítulos anteriores mostramos cómo una matriz con valores en un quantale V —preorden monoidal cerrado con todas las uniones— representa un sistema de puntos interrelacionados y conexiones entre ellos, como un profunctor. El quantale nos dio la estructura y axiomas que necesitábamos para que la multiplicación matricial funcionara correctamente. Pero sabemos por el Ejemplo 5.39 que los cuantales son ejemplos de plataformas, y de hecho la multiplicación matricial tiene sentido en cualquier plataforma R. En el Ejemplo 5.40, explicamos que el conjunto Mat\(_{n}\) (R) de matrices (n × n) en R se puede ensamblar naturalmente en una plataforma, para cualquier elección fija de n\(\in\)\(\mathbb{N}\). Pero, ¿y si queremos hacerlo mejor, y ensamblar todas las matrices en una sola estructura algebraica? ¡El resultado es un utilete!
Una matriz (m × n) M con valores en R es una función M: (\(\underline{m}\)×\(\underline{n}\)) → R. Dada una matriz (m × n) M y una matriz (n × p) N, su compuesto es la matriz (m × p) M; N definida de la siguiente manera para cualquier a \(\in\)\(\underline{m}\)y c\(\in\)\(\underline{p}\):
\(M \text { ; } N(a, c):=\sum_{b \in \underline{n}} M(a, b) \times N(b, c)\)(5.48)
Aquí el\(\Sigma\)\(_{b \in \underline{n}}\) justo significa adición repetida (usando la operación R's + de la plataforma), como de costumbre.
OBSERVACIÓN 5.49. Convencionalmente, se considera generalmente una matriz A que actúa sobre un vector v por multiplicación en el orden Av, donde v es un vector de columna. De acuerdo con nuestra convención de composición, usamos el orden opuesto, v; A, donde v es un vector de fila. Véase por ejemplo la Ec. (5.52) para cuando esto se usa implícitamente.
Deja que R sea una plataforma. Definimos el prop de R-matrices, denotadas Mat (R), para ser el prop cuyos morfismos m → n son las matrices (m × n) con valores en R. La composición de los morfismos viene dada por la multiplicación matricial como en la Ec. (5.48). El producto monoidal viene dado por la suma directa de matrices: matrices dadas A: m → n y b: p → q, definimos A + B: m + p → n + q a ser la matriz de bloques
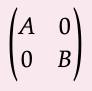
donde cada 0 representa una matriz de ceros de la dimensión apropiada (m × q y n × p). Nos referimos a cualquier combinación de multiplicación y suma directa como interconexión de matrices.
Sea A y B las siguientes matrices con valores en\(\mathbb{N}\):

¿Cuál es la matriz de suma directa A + B? ♦
Convertir gráficos de flujo de señal en matrices
Consideremos ahora más cuidadosamente a qué nos referimos cuando hablamos del significado, o semántica, de cada gráfica de flujo de señal. Vamos a usar matrices.
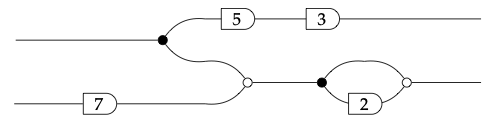
En los ejemplos como los anteriores (copiados de la ecuación (5.1)), las señales que emanan de los cables de salida, digamos a y b, vienen dadas por ciertas sumas de valores de entrada amplificados, digamos x e y. Si solo podemos medir las señales de entrada y salida, y no nos importa lo que suceda en el medio, entonces cada gráfico de flujo de señal bien puede reducirse a una matriz de amplificaciones. Podemos representar el gráfico de flujo de señal de la ecuación (5.1) ya sea por la matriz de la izquierda (para más detalles) o la matriz de la derecha si las etiquetas son claras del contexto:
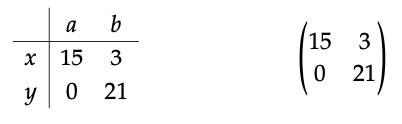
Cada gráfico de flujo de señal se puede interpretar como una matriz.
Los generadores G\ (_ {R}\) de la Definición 5.45 se muestran nuevamente en la siguiente tabla, donde cada uno se interpreta como una matriz.
Por ejemplo, interpretamos la amplificación por una\(\in\) R como la matriz 1 × 1 (a): 1 → 1: es una operación que toma una entrada x\(\in\) R y devuelve una ∗ x. De igual manera, podemos interpretar que\(\supset \text { as the } 2 \times 1 \text { matrix }\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \text { : }\) es una operación que toma un vector de fila que consta de dos entradas 1, x e y, y devuelve x + y. Aquí hay una tabla que muestra la interpretación de cada generador.
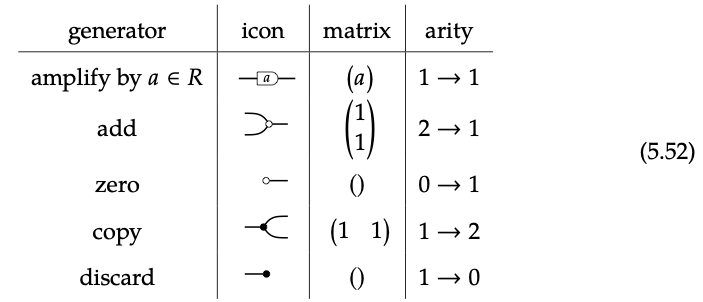
Tenga en cuenta que tanto el cero como el descarte están representados por matrices vacías, pero de dimensiones diferentes. En álgebra lineal es inusual considerar matrices de la forma 0 × n o n × 0 para que varios n sean diferentes, pero se pueden mantener distintas para fines de contabilidad: se puede multiplicar una matriz de 0 × 3 por una matriz de 3 × n para cualquier n, pero no se puede multiplicarlo por una matriz de 2 × n.
Dado que los gráficos de flujo de señal son morfismos en un prop libre, la tabla en (5.52) es suficiente para mostrar que podemos interpretar cualquier diagrama de flujo de señal como una matriz.
Hay un prop functor S: SFG\(_{R}\) → Mat (R) que envía los generadores g\(\in\) G iconos a las matrices como se describe en la Tabla 5.52.
Comprobante. Esto se desprende inmediatamente de la propiedad universal de los apoyos libres, Observación 5.34. \(\square\)
Ahora hemos construido una matriz S (g) a partir de cualquier gráfico de flujo de señal g. Pero, ¿cómo podemos producir esta matriz de manera explícita? Tanto para el gráfico de flujo de señal de ejemplo en la Ec. (5.1) como para los generadores en la Definición 5.45, la matriz asociada tiene dimensión m × n, donde m es el número de entradas y n el número de salidas, con (i, j) ésima entrada describiendo la amplificación de la i-ésima entrada que contribuye a la j ésima salida. Así es como uno esperaría o esperaría que el functor S funcione en general; pero ¿lo hace? Hemos utilizado un martillo grande, la propiedad universal de las construcciones libres para obtener nuestro functor S. Nuestro siguiente objetivo es comprobar que funciona de la manera esperada. Hacerlo es una cuestión de usar la inducción sobre el conjunto de expresiones prop, como vemos ahora. \(^{10}\)
Sea g un gráfico de flujo de señal con m entradas y n salidas. La matriz S (g) es la matriz (m × n) cuya entrada (i, j) describe la amplificación de la i-ésima entrada que contribuye a la j ésima salida.
Comprobante. Recordemos de la Definición 5.30 que una expresión de prop\(_{R}\) generada por G arbitraria se construye a partir de los morfismos id\(_{0}\): 0 → 0, id\(_{1}\): 1 → 1, σ: 2 → 2, y los generadores en G R, usando las siguientes dos reglas:
• si α: m → n y β: p → q son expresiones, entonces (α + β): (m + p) → (n + q) es una expresión.
• si α: m → n y β: n → p son expresiones, entonces α; β: m → p es una expresión. S es un funtor prop por el Teorema 5.53, que por la Definición 5.11 debe preservar identidades, composiciones, productos monoidales y simetrías. Primero mostramos que la proposición es verdadera cuando g es igual a id\(_{0}\)\(_{1}\), id y σ.
El gráfico de flujo de señal vacío id\(_{0}\): 0 → 0 debe enviarse a la matriz única (vacía) (): 0 → 0.
Los morfismos id\(_{1}\), σ y un mapa\(\in\) R a la matriz de identidad, la matriz de intercambio y la matriz escalar (a) respectivamente:
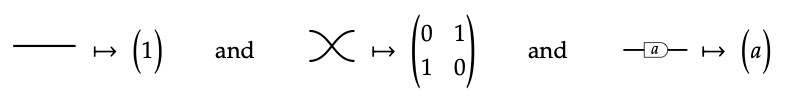
En cada caso, la entrada (i, j) da la amplificación de la i-ésima entrada a la j ésima salida. Queda por mostrar que si la proposición se mantiene para α: m → n y β: p → q, entonces
mantiene para (i) α; β (cuando n = p) y para (ii) α + β (en general). Para probar (i), considere el siguiente cuadro de α; β:
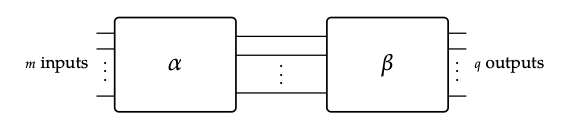
Aquí α: m → n y β: n → q son gráficas de flujo de señal, que se supone obedecen a la proposición. Considere la i-ésima entrada y la k-ésima salida de α; β; simplemente llamaremos a estos i y k. Queremos mostrar que la amplificación que i contribuye a k es la suma, en todos los caminos de i a k, de la amplificación a lo largo de ese camino. Así que también arreglemos algunos j ∈ n, y consideremos rutas de i a k que corren a través de j. Por distributividad de la plataforma R, la amplificación total de i a k a j es la amplificación total en todas las rutas de i a j veces la amplicación total en todas las rutas de j a k. Dado que todas las rutas de i a k deben correr a través de alguna j ésima salida de α/entrada de β, la amplificación que contribuye i a k es
\(\sum_{j \in \underline{n}} \alpha(i, j) * \beta(j, k)\)
Esta es exactamente la fórmula para la multiplicación matricial, que es la composición S (α); S (β) en el prop Mat (R); ver Definición 5.50. Entonces α; β obedece a la proposición cuando α y β lo hacen.
Demostrar (ii) es más sencillo. El producto monoidal α + β de los gráficos de flujo de señal se ve así:
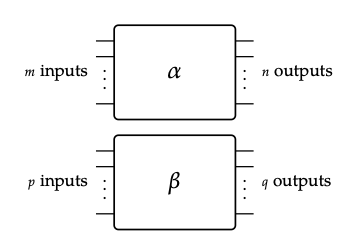
No se crean nuevas rutas; el único cambio es reindexar las entradas y salidas. En particular, la i-ésima entrada de α es la i-ésima entrada de α + β, la j ésima salida de α es la j ésima salida de α + β, la i-ésima entrada de β es la salida (m + i) ésima de α + β, y la j ésima salida de β es la ( n + j) ésima salida de α + β. Esto significa que la matriz con (i, j) ésima entrada que describe la amplificación de la i-ésima entrada que contribuye a la j ésima salida es S (α) + S (β) = S (α + β), como en la Definición 5.50. Esto prueba la proposición. \(\square\)
1. ¿Qué matriz hace el gráfico de flujo de señal?
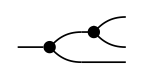
representar?
2. ¿Qué pasa con el gráfico de flujo de señal
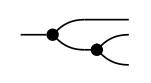
3. ¿Son iguales? ♦
La idea de la semántica funcionaria
Detengámonos un momento para reflexionar sobre lo que acabamos de aprender. Primero, los diagramas de flujo de señal son los morfismos en un prop. Esto significa que tenemos dos operaciones especiales que podemos hacer para formar nuevos diagramas de flujo de señal a partir de los antiguos, a saber, la composición (combinando en serie) y el producto monoidal (combinando en paralelo). Podríamos pensar en esto como especificar una 'gramática' o 'sintaxis' para diagramas de flujo de señales.
Como lenguaje, los gráficos de flujo de señal no solo tienen sintaxis sino también semántica: cada diagrama de flujo de señal puede interpretarse como una matriz. Además, las matrices tienen la misma estructura gramatical: forman un puntal, y podemos construir nuevas matrices a partir de viejas usando composición y producto monoidal. En el Teorema 5.53 se completó esta imagen mostrando que la interpretación semántica es un funtor prop entre el prop de gráficos de flujo de señal y el prop de matrices. Así decimos que las matrices dan semántica funcionaria para diagramas de flujo de señales.
La semántica funcionaria es una manifestación clave de la composicionalidad. Dice que la matriz que significa S (g) para un gráfico de flujo de señal grande g se puede calcular por:
- dividiendo g en trozos pequeños,
- computar las matrices muy simples para cada pieza, y
- utilizando multiplicación matricial y suma directa para volver a juntar las piezas para obtener el significado deseado, S (g).
Esta funcionalidad es útil en la práctica, por ejemplo para acelerar el cálculo de la semántica de los gráficos de flujo de señal: para gráficos de flujo de señal grandes, componer matrices es mucho más rápido que trazar rutas.


