5.4: Álgebra lineal gráfica
- Page ID
- 112172
En esta sección comenzaremos a desarrollar algo llamado álgebra lineal gráfica, que extiende las ideas anteriores. Este formalismo es en realidad bastante poderoso. Por ejemplo, con él podemos probar fácil y gráficamente ciertas conjeturas a partir de la teoría del control que, aunque finalmente se resolvieron, requirieron argumentos de álgebra matricial bastante elaborados [FSR16].
presentación de Mat (R)
Que R sea una plataforma, como se define en la Definición 5.36. El teorema principal de la sección anterior, Teorema 5.53, proporcionó un functor S: SFG\(_{R}\) → Mat (R) que convierte cualquier flujo de señal
grafica en una matriz. A continuación mostramos que S está “lleno”: que cualquier matriz puede ser representada por un gráfico de flujo de señal.
Dada cualquier matriz M\(\in\) Mat (R), existe un gráfico de flujo de señal g\(\in\) SFG\(_{R}\) tal que tal que S (g) = M.
Croquis de prueba. Deje que M\(\in\) Mat (R) sea una matriz (m × n). Queremos un gráfico de flujo de señal g tal que S (g) = M. En particular, para calcular S (g) (i, j), sabemos que podemos simplemente calcular la amplificación que la i-ésima entrada contribuye a la j ésima salida. La idea clave entonces es construir g de manera que haya exactamente una ruta desde la i-ésima entrada hasta la j ésima salida, y que esta ruta tenga exactamente un icono de multiplicación escalar, es decir, M (i, j).
La construcción general es un poco técnica (ver Ejercicio 5.59), pero la idea es clara al solo considerar el caso de 2 × 2-matrices.
Supongamos que M es la matriz 2 × 2\(\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) .\) Entonces definimos g para que sea el gráfico de flujo de señal
Trazando caminos, es fácil ver que S (g) = M. Obsérvese que g es el compuesto de cuatro capas, cada capa, respectivamente, un producto monoidal de (i) mapas de copia y descarte, (ii) multiplicaciones escalares, (iii) swaps e identidades, (iv) mapas de suma y cero. Para el caso general, véase Ejercicio 5.59. \(\square\)
Dibuje gráficas de flujo de señal que representen las siguientes matrices:
Anote un comprobante detallado de la Proposición 5.56. Supongamos que M es una matriz m × n. Siga la idea del caso (2 × 2) en la ecuación (5.57), y construya el gráfico de flujo de señal g que tenga m entradas y n salidas como el compuesto de cuatro capas, comprendiendo respectivamente (i) mapas de copia y descarte, (ii) escalares, (iii) swaps e identidades, (iv) mapas de suma y cero . ♦
También podemos usar la Proposición 5.56 y su prueba para dar una presentación de Mat (R), que se definió en la Definición 5.50.
El prop Mat (R) es isomórfico al puntal con la siguiente presentación. El conjunto de generadores es el conjunto
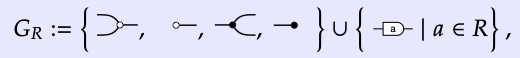
él mismo que el conjunto de generadores para SFG R; ver Definición 5.45. Tenemos las siguientes ecuaciones para cualquier a, b ∈ R:
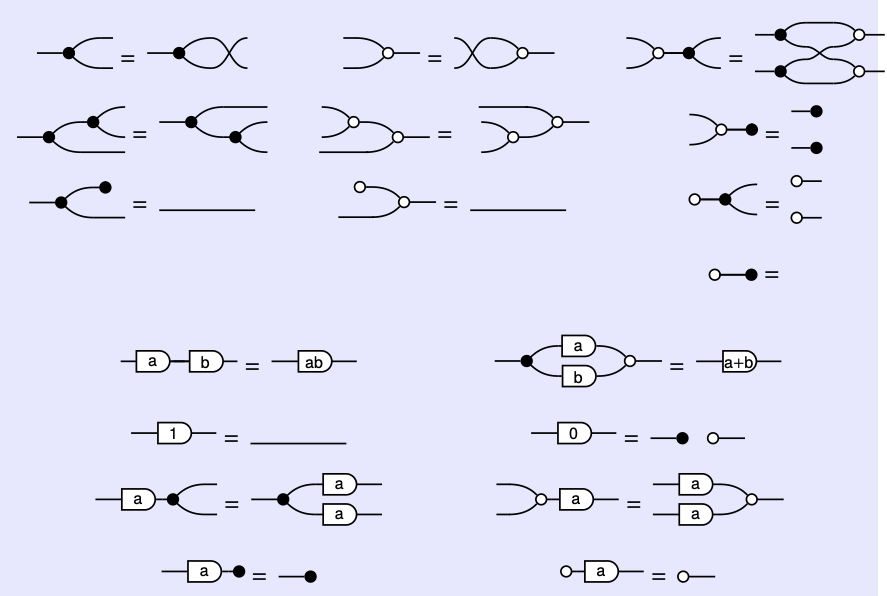
Prueba. La idea clave es que estas ecuaciones son suficientes para reescribir cualquier expresión de prop generada por G R en una forma normal —la utilizada en la prueba de la Proposición 5.56— con todos los nodos negros a la izquierda, todos los nodos blancos a la derecha y todos los escalares en el medio. Esto es suficiente para mostrar la igualdad de dos expresiones cualesquiera que representen la misma matriz. Los detalles se pueden encontrar en [BE15] o [BS17]\(\square\)
Sonido y presentación completa de matrices. Una vez que te acostumbras a ello, Teorema 5.60 proporciona una manera intuitiva y visual de razonar sobre las matrices. En efecto, el teorema implica que dos gráficas de flujo de señal representan la misma matriz si y solo si una puede ser convertida en la otra mediante la aplicación local de las ecuaciones anteriores y los axiomas prop.
El hecho de que puedas demostrar que dos SFG son iguales usando solo reglas gráficas se puede afirmar en la jerga de la lógica: decimos que las reglas gráficas proporcionan un sistema de razonamiento sólido y completo. Para ser más específicos, el sonido se refiere a la dirección hacia delante de la declaración anterior: dos gráficas de flujo de señal representan la misma matriz si una se puede convertir en la otra usando las reglas dadas. Completa se refiere a la dirección inversa: si dos gráficas de flujo de señal representan la misma matriz, entonces podemos convertir una en la otra usando las ecuaciones del Teorema 5.60.
Ambos gráficos de flujo de señal a continuación representan la misma matriz,\(\left(\begin{array}{l} 0 \\ 6 \end{array}\right):\)
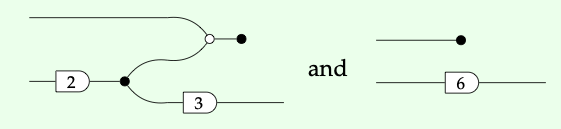
Esto significa que uno puede transformarse en el otro utilizando únicamente las ecuaciones del Teorema 5.60. En efecto, aquí
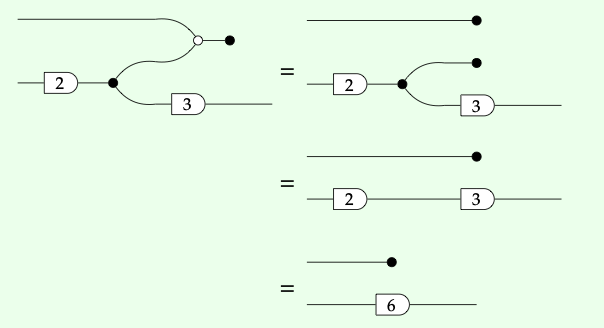
1. Para cada matriz en el Ejercicio 5.58, dibuje otro gráfico de flujo de señal que represente esa matriz.
2. Usando las ecuaciones anteriores y los axiomas prop, probar que los dos gráficos de flujo de señal representan la misma matriz. ♦
Considere los gráficos de flujo de señal
- Dejar R = (\(\mathbb{N}\), 0, +, 1, ∗). Al examinar la presentación de Mat (R) en el Teorema 5.60, y sin computar las matrices que representan las dos gráficas de flujo de señal en la Ec. (5.64), se demuestra que no representan la misma matriz.
- Ahora supongamos que el rig es R =\(\mathbb{N}\) /3\(\mathbb{N}\); si no sabes lo que esto significa, solo reemplaza todos los 3's por 0's en el diagrama de la derecha de la Ec. (5.64). Encuentra lo que llamarías una representación mínima de este diagrama, utilizando la presentación en Teorema 5.60. ♦
Aparte: objetos monoides en una categoría monoidal
Varios subconjuntos de las ecuaciones en el Teorema 5.60 codifican estructuras que son familiares de muchas otras partes de las matemáticas, por ejemplo, la teoría de la representación. Por ejemplo, se pueden encontrar los axiomas para (co) monoides, (co) homomorfismos monoides, álgebras de Frobenius y (con un poco reordenando) álgebras Hopf, sentados dentro de esta colección. El primer ejemplo, la noción de monoides, ya nos resulta particularmente familiar, por lo que lo discutimos brevemente a continuación, tanto en términos algebraicos (Definición 5.65) como en términos diagramáticos (Ejemplo 5.68).
Un objeto monoide (M, μ, η) en una categoría monoidal simétrica (C, I,) es un objeto M de C junto con morfismos μ: M M → M y η: I → M tal que
(a) (μ id); μ = (id μ); μ y
b) (η id); μ = id = (id η); μ.
Un objeto monoide conmutativo es un objeto monoide que obedece aún más
(c) σ\(_{M,M}\); μ = μ.
donde σ\(_{M,M}\) es el mapa swap en M en C. A menudo lo denotamos simplemente por σ.
Los objetos monoides se denominan así porque son una abstracción del concepto habitual de monoide.
Un objeto monoide en (Set, 1, ×) es solo un monoide antiguo regular, como se define en el Ejemplo 2.6; véase también Ejemplo 3.13.
Es decir, es un conjunto M, una función μ: M × M → M, que denotamos por notación infija ∗, y un elemento η (1)\(\in\) M, que denotamos por e, satisfaciendo (a ∗ b) ∗ c = a ∗ b ∗ c) y a ∗ e = a = e ∗ a.
Considera el conjunto\(\mathbb{R}\) de números reales.
- Mostrar que si μ:\(\mathbb{R}\) ×\(\mathbb{R}\) →\(\mathbb{R}\) está definido por μ (a, b) = a ∗ b y si η\(\in\)\(\mathbb{R}\) se define como η = 1, entonces (\(\mathbb{R}\), ∗, 1) satisface las tres condiciones de la Definición 5.65.
- Mostrar que si μ:\(\mathbb{R}\) ×\(\mathbb{R}\) →\(\mathbb{R}\) está definido por μ (a, b) = a + b y si η\(\in\)\(\mathbb{R}\) se define como η = 0, entonces (\(\mathbb{R}\), +, 0) satisface las tres condiciones de la Definición 5.65. ♦
Gráficamente, podemos representar
. Entonces los axiomas (a), (b) y (c) de la Definición 5.65 se convierten en:
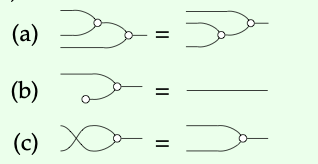
Los tres se encuentran en el Teorema 5.60. Así podemos concluir de inmediato lo siguiente: el triple
es un objeto monoide conmutativo en el prop Mat (R).
Para cualquier plataforma R, hay un functor U: Mat (R) → Set, enviando el objeto n\(\in\)\(\mathbb{N}\) al conjunto R\(^{n}\), y enviando un morfismo (matriz) M: m → n al función R\(^{m}\) → R\(^{n}\) dada por multiplicación vector-matriz.
Recordemos que en Mat (R), la unidad monoidal es 0 y el producto monoidal es +, porque es un puntal. Recordemos también que en (la estructura monoidal habitual en) Set, la unidad monoidal es {1}, un conjunto con un elemento, y el producto monoidal es × (ver Ejemplo 4.49).
- Comprobar que el functor U: Mat (R) → Set, definido anteriormente, conserva la unidad monoidal y el producto monoidal.
- Mostrar que si (M, μ, η) es un objeto monoide en Mat (R) entonces (U (M), U (μ), U (η)) es un objeto monoide en Set. (Esto funciona para cualquier funtor monoidal —que definiremos en la Definición 6.68— no solo para U en particular).
- En el Ejemplo5.68, dijimos que el triple es un objeto monoide conmutativo en el prop Mat (R). Si R =\(\mathbb{R}\) es el rig de números reales, esto significa que tenemos una estructura monoide en el set\(\mathbb{R}\). Pero en el Ejercicio 5.67 dimos dos estructuras monoides de este tipo. ¿Cuál es? ♦
El triple en Mat (R) forma un objeto monoide conmutativo en Mat (R) op. De ahí también decimos que forma un objeto comonoide coconmutativo en Mat (R).
Una categoría monoidal estricta simétrica, es sólo un objeto monoide conmutativo en (Cat, ×, 1). Desempaquetaremos esto en la Sección 6.4.1.
Un preorden monoidal simétrico, que definimos en la Definición 2.2, es solo un objeto monoide conmutativo en la categoría monoidal simétrica (Preord, ×, 1) de preordenes y mapas monótonos.
Para quienes saben qué son (o pueden adivinar) los productos tensores de los monoides conmutativos: Una plataforma es un objeto monoide en la categoría monoidal simétrica (CMon,,\(\mathbb{N}\)) de monoides conmutativos con producto tensor.
OBSERVACIÓN 5.74. Si presentamos un prop M usando dos generadores μ: 2 → 1 y η: 0 → 1, y las tres ecuaciones de la Definición 5.65, podríamos llamarlo 'la teoría de los monoides en categorías monoidales'. Esto quiere decir que en cualquier categoría monoidal C, los objetos monoides en C corresponden a estrictos funtores monoidales M → C. Este tipo de idea lleva al estudio de las teorías algebraicas, debido a Bill Lawvere y extendido por muchos otros; ver Sección 5.5.
Gráficos de flujo de señal: retroalimentación y más
En este punto de la historia, hemos visto que cada gráfico de flujo de señal representa una matriz, y esto nos da una nueva forma de razonar sobre las matrices. Esto es solo el comienzo de un hermoso cuento, uno no solo de matrices gráficas, sino de álgebra lineal gráfica. Cerramos este capítulo con algunas breves pistas sobre cómo continúa la historia.
La naturaleza pictórica de los gráficos de flujo de señal nos invita a jugar con ellos. Si bien normalmente dibujamos el icono de copia así
,, podríamos invertirlo fácilmente y dibujar un icono
. ¿Qué podría significar? Pensemos de nuevo en la semántica de los gráficos de flujo.
El enfoque conductual. Un gráfico de flujo de señal g: m → n toma una entrada x\(\in\) R\(^{m}\) y da una salida y\(\in\) R\(^{n}\). De hecho, dado que esto es todo lo que nos importa, podríamos pensar en representar un gráfico de flujo de señal g como describir un conjunto de pares de entrada y salida (x, y).
Llamaremos a este conjunto el comportamiento de g y lo denotaremos B (g)\(\subseteq\) R\(^{m}\) × R\(^{n}\). Por ejemplo, el gráfico de flujo 'copiar'
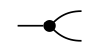
envía la entrada 1 a la salida (1, 1), por lo que consideramos (1, (1, 1)) como un elemento de copia-comportamiento. Del mismo modo, (x, (x, x)) es el comportamiento de copia para cada x\(\in\) R, así tenemos
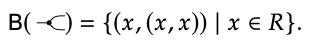
En resumen, el gráfico de flujo de señal g: m → n tiene el comportamiento
\(\mathrm{B}(g)=\left\{(x, S(g)(x)) \mid x \in R^{m}\right\} \subseteq R^{m} \times R^{n}\)(5.75)
Imagen especular de un icono. La perspectiva conductual anterior proporciona una pista sobre cómo interpretar las imágenes especulares de los diagramas discutidos anteriormente.
Al invertir un icono g: m → n intercambia las entradas con las salidas, así que si denotamos este icono invertido por g\(^{op}\), debemos tener g\(^{op}\): n → m. Así que si B (g)\(\subseteq\) R\(^{m}\) × R\(^{n}\) entonces necesitamos B (g\(^{op}\))\(\subseteq\) R\(^{m}\) × R\(^{n}\). Una forma sencilla de hacer esto es reemplazar cada (a, b) por (b, a), así tendríamos
\ (\ comenzar {ecuación}
\ mathrm {B}\ izquierda (g^ {\ mathrm {op}}\ derecha) :=\ izquierda\ {(S (g) (x) (x), x)\ media x\ en R^ {m}\ derecha\}\ subseteq R^ {n}\ veces R^ {m}
\ final {ecuación}\) (5.76)
A esto se le llama la relación transpuesta.
1. ¿Cuál es el comportamiento B () del icono de suma invertida: 1→ 2?
2. ¿Cuál es el comportamiento B () del icono de copia invertida,: 2→ 1? ♦
Las ecuaciones (5.75) y (5.76) nos dan fórmulas para interpretar gráficos de flujo de señal y sus imágenes especulares. Pero esto fácilmente llevaría a la decepción, si no pudiéramos combinar las dos direcciones conductual; afortunadamente podemos.
Combinando direcciones. Cuál debe ser el comportamiento para un diagrama como el siguiente:
Formalicemos un poco nuestros pensamientos y comencemos por pensar en comportamientos. El comportamiento de un gráfico de flujo de señal m → n es un subconjunto B\(\subseteq\) R\(^{m}\) × R\(^{n}\), es decir, una relación. ¿Por qué no intentar construir un puntal donde los morfismos m → n son relaciones?
Necesitaremos saber componer y tomar productos monoidales de las relaciones. Y si queremos que este puntal de relaciones contenga el viejo prop Mat (R), necesitamos las nuevas composiciones y productos monoidales para generalizar los antiguos en Mat (R). Dadas las gráficas de flujo de señal con matrices M: m → n y N: n → p, vemos que sus comportamientos son las relaciones\(B_{1}\) := {(x, Mx) | x\(\in\)\(R^{m}\)} y\(B_{2}\) := {(y, Ny) | y\(\in\)\(R^{n}\), mientras el comportamiento de M; N es la relación {(x, x; M; N) | x\(\in\)\(R^{m}\)}. Este es un caso de composición de relaciones. Dadas las relaciones\(B_{1}\)\(\subseteq\) R\(^{m}\) ×\(B_{2}\)\(\subseteq\) R\(^{n}\) y R\(^{n}\) × R\(^{p}\), su compuesto\(B_{1}\);\(B_{2}\)\(\subseteq\) R \(^{m}\)× R\(^{p}\) viene dada por
\(B_{1} \text { ; } B_{2}:=\left\{(x, z) \mid \text { there exists } y \in R^{n} \text { such that }(x, y) \in B_{1} \text { and }(y, z) \in B_{2}\right\}\)(5.78)
Lo usaremos como definición general para componer dos comportamientos.
Que R sea una plataforma. Definimos el prop Rel\(_{R}\) de relaciones R para tener subconjuntos B\(\subseteq\) R\(^{m}\) × R\(^{n}\) como morfismos. Estos están compuestos por la regla de composición de la Ec. (5.78), y tomamos el producto de dos juegos para formar su producto monoidal.
En Definición 5.79 pasamos rápidamente por productos monoidales + en el prop Rel\(_{R}\). Si B\(\subseteq\) R\(^{m}\) × R\(^{n}\) y C\(\subseteq\) R\(^{n}\) × R\(^{p}\) son morfismos en Rel\(_{R}\), anote B + C en notación de conjunto. ♦
Gráficos de flujo de señal (Ya no simplificados). Recordemos que anteriormente, por ejemplo en la Definición 5.45, escribimos G R para el conjunto de generadores de gráficos de flujo de señal. En la Sección 5.4.3, escribimos g\(^{op}\) para la imagen especular de g, por cada \(\in\)g\(_{R}\) G. Entonces escribamos G\(_{R}\) := {g\(^{op}\) | g\(\in\) G\(_{R}\)} para el conjunto de todas las imágenes especulares de generadores. Definimos un prop
\(\mathbf{S F G}_{R}^{+}:=\text {Free }\left(G_{R} \sqcup G_{R}^{\mathrm{op}}\right)\)(5.81)
Llamamos a un morfismo en el prop\(\mathbf{S F G}_{R}^{+}\) un gráfico de flujo de señal a (no simplificado): estos extienden nuestros gráficos de flujo de señal simplificados de la Definición 5.45 porque ahora también podemos usar los iconos reflejados. Por la propiedad universal de los apoyos libres, ya que hemos dicho cuál es el comportamiento de los generadores (el comportamiento de un icono invertido es la relación transpuesta; ver Eq. (5.76)), hemos especificado el comportamiento de cualquier gráfico de flujo de señal. Los siguientes dos ejercicios nos ayudan a entender en qué consiste este comportamiento.
Dejar g: m → n, h:l → n sean gráficos de flujo de señal. Tenga en cuenta que h\(^{op}\): n → l es un gráfico de flujo de señal, y podemos formar el compuesto g; (h\(^{op}\)):
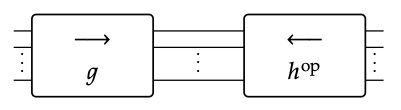
Mostrar que el comportamiento de g; (h\(^{op}\))\(\subseteq\) R\(^{m}\) × R\(^{l}\) es igual a
\(\mathrm{B}\left(g \text { ; }\left(h^{\mathrm{op}}\right)\right)=\{(x, y) \mid S(g)(x)=S(h)(y)\}\)♦
Dejar g: m → n, h: m → p sean gráficos de flujo de señal. Tenga en cuenta que (g\(^{op}\)): n → m es un gráfico de flujo de señal, y podemos formar el compuesto g\(^{op}\); h
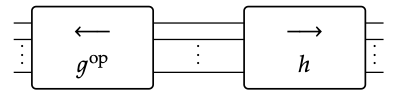
Mostrar que el comportamiento de g\(^{op}\); h es igual a
\(\mathrm{B}\left(\left(g^{\mathrm{op}}\right) ; h\right)=\left\{(S(g)(x), S(h)(x)) \mid x \in R^{m}\right\}\)♦
Álgebra lineal a través de gráficos de flujo de señal. En la Ec. (5.75) vemos que cada matriz, o mapa lineal, puede representarse como el comportamiento de un gráfico de flujo de señal, y en el Ejercicio 5.82 vemos que también se pueden representar conjuntos de soluciones de ecuaciones lineales. Esto incluye conceptos centrales en álgebra lineal, como núcleos e imágenes.
Aquí hay un ejercicio para aquellos que conocen álgebra lineal, en particular núcleos y cokernels.
Sea R un campo, que g: m → n sea un gráfico de flujo de señal, y que S (g)\(\in\) Mat (R) sea la matriz asociada (m × n) (ver Teorema 5.53).
1. Demostrar que el compuesto de g con 0-reverses, se muestra aquí
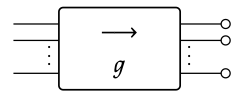
es igual al núcleo de la matriz S (g).
2. Mostrar que el compuesto de descarte-invierte con g, se muestra aquí
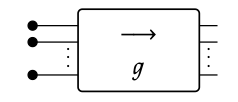
es igual a la imagen de la matriz S (g).
3. Mostrar que para cualquier gráfica de flujo de señal g, el subconjunto B (g)\(\subseteq\) R\(^{m}\) × R\(^{n}\) es un subespacio lineal.
Es decir, si b\(_{1}\), b\(_{2}\)\(\in\) B (g) entonces también lo son b\(_{1}\) + b\(_{2}\) y r ∗ b\(_{1}\), para cualquier r\(\in\) R. ♦
Hemos visto así que las gráficas de flujo de señales proporcionan un lenguaje uniforme y compositivo para hablar de muchos conceptos en álgebra lineal. Además, en el Ejercicio 5.84 mostramos que el comportamiento de un gráfico de flujo de señal es una relación lineal, es decir, una relación cuyos elementos se pueden sumar y multiplicar por escalares \(\in\)r R. De hecho, lo contrario también es cierto: cualquier relación lineal B\(\subseteq\) R\(^{m}\) × R\(^{n}\) puede ser representada por un gráfico de flujo de señal.
Uno podría querer mostrar que las relaciones lineales en R forman un prop, LineRel\(_{R}\). Es decir, uno podría querer mostrar que hay un sub-prop del prop \(_{R}\)Rel de la Definición 5.79, donde los morfismos m → n son los subconjuntos B\(\subseteq\) R\(^{m}\) × R\(^{n}\) tal que B es lineal.
Es decir, donde para cualquier (x, y)\(\in\) B y r\(\in\) R, el elemento (r ∗ x, r ∗ y)\(\in\) R\(^{m}\) × R\(^{n}\) está en B, y para cualquier (x′, y ′)\(\in\) B, el elemento (x + x ′, y + y ′) está en B.
Esto es ciertamente factible, pero para este ejercicio, sólo pedimos que demuestre que el compuesto de dos relaciones lineales es lineal. ♦
Así como dimos una presentación sonora y completa para el prop de matrices en el Teorema 5.60, es posible dar una presentación sonora y completa para las relaciones lineales sobre R. Además, es posible dar tal presentación cuya operación generadora
set es G R G R como en la Ec. (5.81) y cuyas ecuaciones incluyen las del Teorema 5.60, más algunas más algunas más. Esta presentación da un método gráfico para hacer álgebra lineal: una ecuación entre subespacios lineales es verdadera si y solo si se puede probar usando las ecuaciones de la presentación.
Aunque no es difícil, dejamos la presentación completa para mayor lectura (Sección 5.5). En cambio, concluiremos nuestra exploración del apuntalamiento de las relaciones lineales señalando que algunas de estas 'pocas más' ecuaciones establecen que las relaciones al igual que los problemas de co-diseño en el Capítulo 4 forman una categoría cerrada compacta.
Estructura compacta cerrada. Usando los iconos disponibles para los gráficos de flujo de señal, podemos construir morfismos que se parecen a la 'copa' y 'tapa' de la Definición 4.58:
Los comportamientos de estas gráficas son respectivamente
\(\{(0,(x, x)) \mid x \in R\} \subseteq R^{0} \times R^{2} \quad \text { and } \quad\{((x, x), 0) \mid x \in R\} \subseteq R^{2} \times R^{0}\)
De hecho, estos muestran que el objeto 1 en el prop Rel\(_{R}\) es dual consigo mismo: los morfismos de la Eq. (5.86) sirven como η\(_{1}\) y ε\(_{1}\) de la Definición 4.58. Utilizando productos monoidales de estos morfismos, se puede demostrar que cualquier objeto en Rel\(_{R}\) es dual consigo mismo.
Gráficamente, esto significa que los tres gráficos de flujo de señal
todos representan la misma relación.
Usando estas relaciones, es sencillo verificar el siguiente resultado.
El prop Rel\(_{R}\) es una categoría compacta cerrada en la que cada objeto n\(\in\)\(\mathbb{N}\) es dual consigo mismo, n = n\(^{∗}\).
Para simplificar nuestros gráficos de flujo de señal, definimos nuevos iconos cup and cap por las ecuaciones
Volver a la teoría del control. Terminemos pensando en cómo representar un problema de teoría de control simple en este escenario. Supongamos que queremos diseñar un sistema para mantener la velocidad de un automóvil a una velocidad deseada u. Trabajaremos en diagramas de flujo de señal sobre la plataforma\(\mathbb{R}\) [s, s\(^{−1}\)] de polinomios en s y s\(^{−1}\) con coeficientes en\(\mathbb{R}\) y donde ss\(^{−1}\) = s\(^{−1}\) s = 1. Esto es estándar en la teoría del control: pensamos en s como integración, y s\(^{−1}\) como diferenciación.
Hay tres factores que contribuyen a la velocidad real v. Primero, está la velocidad real v. Segundo, hay fuerzas externas F. Tercero, tenemos nuestro sistema de control: esto tomará alguna combinación lineal a ∗ u + b ∗ v de la velocidad deseada y velocidad real, amplificarla por algún factor p para dar una aceleración (posiblemente negativa). Podemos representar este sistema de la siguiente manera, donde m es la masa del automóvil.
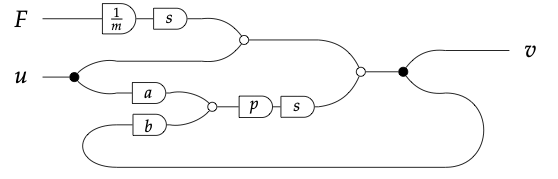
Esto se puede leer como la siguiente ecuación, donde uno señala que v ocurre dos veces:
\(v=\int \frac{1}{m} F(t) d t+u(t)+p \int a u(t)+b v(t) d t\)
Nuestro problema de control entonces pregunta: ¿cómo elegimos a y b para que el comportamiento de esta gráfica de flujo de señal se acerque a la relación {(F, u, v) | u = v}? Al formular problemas de esta manera, podemos usar extensiones de la lógica que hemos discutido anteriormente para razonar sobre problemas tan complejos del mundo real.