6.3: Categorías de Hyper Graph
- Page ID
- 112218
Una categoría de hipergrafía es un tipo de categoría monoidal simétrica cuyos diagramas de cableado son redes. Pronto veremos que los circuitos eléctricos se pueden organizar en una categoría de hipergrafía; esto es lo que hemos estado construyendo. Pero para definir categorías de hipergrafía, es útil introducir primero los monoides de Frobenius.
Monoides de Frobenius
Las imágenes de cospanes que vimos arriba, por ejemplo en la Ec. (6.50) parecen algo así como iconos en las gráficas de flujo de señal (ver Sección 5.3.2): varios cables se fusionan y dividen, inicializan y terminan. Y éstas siguen las mismas reglas que hicieron para las relaciones lineales, que discutimos brevemente en el Ejercicio 5.84. Hay mucho potencial de confusión, así que comencemos de cero y volvamos a construir.
En cualquier categoría monoidal simétrica (C, I,), recuerda de la Sección 4.4.2 que los objetos pueden dibujarse como alambres y los morfismos se pueden dibujar como cajas. Morfismos particularmente notables podrían ser iconificados como puntos en lugar de cajas, para indicar que los morfismos allí no son arbitrarios sino dignos de notación. Un caso de esto es cuando hay un objeto X con “habilidades” especiales, por ejemplo, la capacidad de duplicarse en dos, o desaparecer en la nada. Para hacer esto preciso, recordemos de la Definición 5.65 que un monoide conmutativo (X, μ, η) en categoría monoidal simétrica (C, I,) es un objeto X de C junto con morfismos (notables)
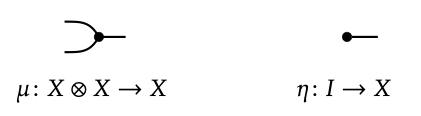
obedeciendo
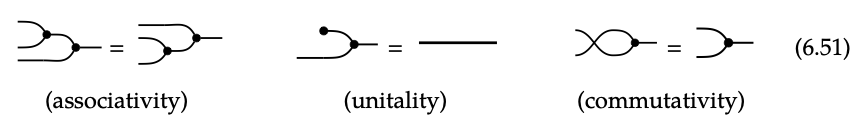
donde está la simetría en X X. Un cocomonoide coconmutativo (X, δ, ε) es un objeto X con mapas δ: X → X X, ε: X → I, obedeciendo las imágenes especulares de las leyes en la Ec. (6.51).
Supongamos que X tiene tanto la estructura de un monoide conmutativo como un comonoide coconmutativo, y considere un diagrama de cableado construido solo a partir de los iconos μ, η, δ y ε, donde cada cable está etiquetado como X. Estos diagramas tienen una izquierda y una derecha, y son imágenes de cómo los puertos de la izquierda están conectados a los puertos de la derecha. El monoide conmutativo y los axiomas comonoides coconmutativos, por lo tanto, ambos expresan cuando considerar dos de tales imágenes de conexión deben considerarse iguales. Por ejemplo, la asociatividad dice que el orden de conexión de los puertos de la izquierda no importa; la coasociatividad (no dibujada) dice lo mismo para la derecha.
Si quieres ir hasta el final y decir “lo único que me importa es qué puerto está conectado a cuál; ni siquiera me importan la izquierda y la derecha”, entonces necesitas algunos axiomas más para decir cómo interactúan los morfismos μ y δ, la fusión y el divisor.
Que X sea un objeto en una categoría monoidal simétrica (C,, I). Una estructura de Frobe- nius en X consiste en una 4-tupla (μ, η, δ, ε) tal que (X, μ, η) es un monoide conmutativo y (X, δ, ε) es un comonoide coconmutativo, que satisface las seis ecuaciones anteriores ((co-) asociatividad, (co-) unitalidad, (co-) conmutatividad), también como las siguientes tres ecuaciones:
Nos referimos a un objeto X equipado con una estructura Frobenius como un monoide Frobenius conmutativo especial, o simplemente monoide de Frobenius para abreviar.
Con estas dos ecuaciones, resulta que dos morfismos X m → X n definidos por componer y tensorar identidades en X y los morfismos notables μ, δ, etc.— son iguales si y solo si sus diagramas de cadena conectan los mismos puertos. Este vínculo entre la conectividad y los monoides de Frobenius se puede precisar de la siguiente manera.
Sea (X, μ, η, δ, ε) un monoide de Frobenius en una categoría monoidal (C, I,). Sea m, n ∈ N. Definir s m, n: X m → X n para ser el siguiente morfismo
Se puede escribir formalmente como (m − 1) μ seguidos de (n − 1) δ, con casos especiales cuando m = 0 o n = 0.
Llamamos a s\(_{m,n}\) la araña de tipo (m, n), y podemos dibujarla de manera más simple como el icono
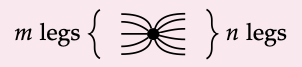
Por lo que un monoide Frobenius conmutativo especial, además de ser un bocado, es un alambre 'spiderable'. Usted acepta que en cualquier categoría monoidal lenguaje de diagrama de cableado, los cables representan objetos y las cajas representan morfismos? Bueno en nuestra forma rara de hablar, si un cable es spiderable, significa que tenemos un montón de morfismos μ, η, δ, ε, σ que podemos combinar sin preocuparnos por el orden de hacerlo: el resultado es simplemente “cuántas entradas, y cuántas salidas”: una araña. Aquí hay una declaración formal.
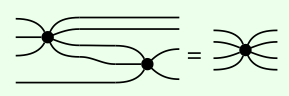
Sea (X, μ, η, δ, ε) un monoide de Frobenius en una categoría monoidal (C, I,). Supongamos que tenemos un mapa f: X m → X n cada uno construido a partir de arañas y el mapa de simetría σ: X 2 → X 2 usando composición y el producto monoidal, y tal que el diagrama de cuerdas de f tiene solo un componente conectado. Entonces es una araña: f = \(_{m,n}\)s.
Como los dos siguientes morfismos ambos (i) tienen el mismo número de entradas y salidas, (ii) se construyen solo a partir de arañas, y (iii) están conectados, el Teorema 6.55 inmediatamente implica que son iguales:
Que X sea un objeto equipado con una estructura Frobenius. ¿Cuáles de los morfismos X X → X X X de la siguiente lista son necesariamente iguales?
♦
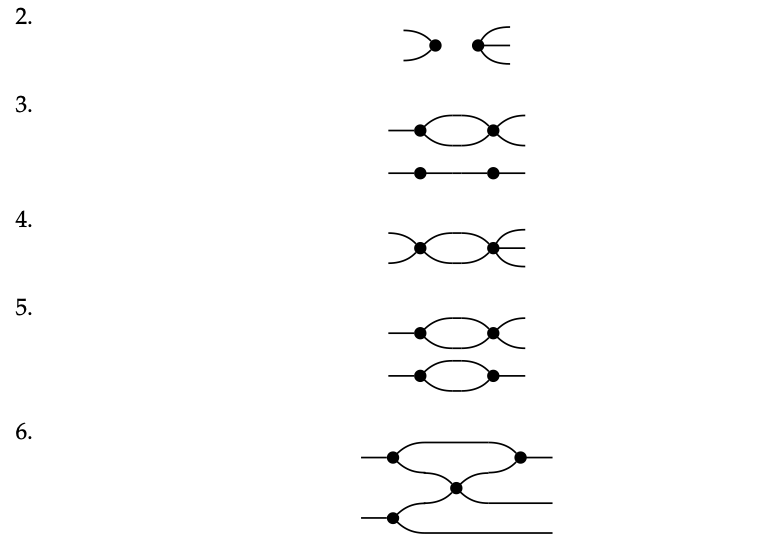Volver a cospans. Otra forma de entender a los monoides de Frobenius es relacionarlos con los cospanes. Recordemos la noción de presentación de prop de la Definición 5.33.
Considere el conjunto de cuatro elementos G: = {μ, η, δ, ε} y defina in, out: G → N de la siguiente manera:
\ (\ begin {array} {cccc}
\ nombreoperador {en} (\ mu) :=2, &\ nombreoperador {en} (\ eta) :=0, &\ nombredeoperador {en} (\ delta) :=1, &\ nombreoperador {en} (\ épsilon) :=1,\\\ nombredeoperador {out} (\ mu) :=1, &
\ operatorname {out} (\ mu) :=1, &\ operatorname {out} (\ mu) :=1, &\ nombre {out} (\ eta) :=1, &\ text {out} (\ delta) :=2, &\ nombreoperador {out} (\ épsilon) :=0.
\ end {array}\)
Sea E el conjunto de axiomas de Frobenius, es decir, las nueve ecuaciones de la Definición 6.52.
Entonces el apuntalamiento libre en (G, E) es equivalente, como categoría monoidal simétrica, a a a Cospan\(_{FinSet}\).
Así vemos que los cables ideales, la conectividad, los cospanes y los objetos con estructuras Frobenius están íntimamente relacionados. Usamos estructuras de Frobenius (todas esas cosas de división, fusión, inicialización y terminación) como una forma de capturar la gramática de los diagramas de circuito.
Diagramas de cableado para categorías de hipergrafos
Introducimos categorías de hipergrafía a través de sus diagramas de cableado. Al igual que para las categorías monoidales, la definición formal es solo la estructura requerida para interpretar sin ambigüedades estos diagramas.
De hecho, nuestro interés por las categorías de hipergrafía se ve mejor en sus diagramas de cableado. La idea clave es que los diagramas de cableado para categorías de hipergrafos sean diagramas de red. Esto significa, además de dibujar cajas etiquetadas con entradas y salidas, como podemos para categorías monoidales, y además de doblar estos cables como podemos para categorías compactas cerradas, se nos permite dividir, unir, terminar e inicializar alambres.
Aquí hay un ejemplo de un diagrama de cableado que representa un compuesto de morfismos en una categoría de hipergrafía
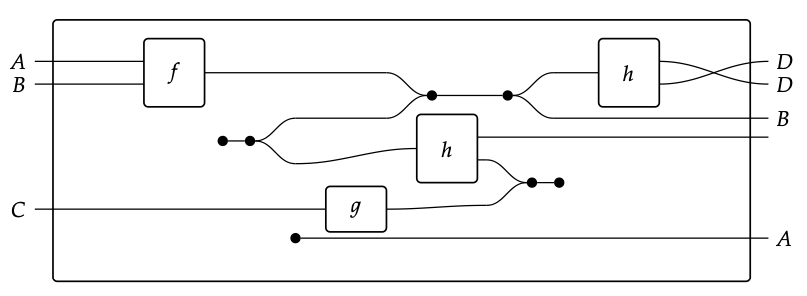
Hemos suprimido algunas de las etiquetas de objeto/cable para su legibilidad, ya que todos los tipos se pueden inferir de las etiquetadas.
1. ¿Qué etiqueta debe estar en la entrada a h?
2. ¿Qué etiqueta debe estar en la salida de g?
3. ¿Qué etiqueta debe estar en el cuarto cable de salida del compuesto? ♦
Así, las categorías de hipergrafía son lo suficientemente generales como para hablar de todos los lenguajes diagramáticos de estilo red, como los diagramas de circuitos.
Definición de categoría de hipergrafía
Ahora estamos listos para definir formalmente las categorías de hipergrafía. Dado que los diagramas de cableado para categorías de hipergrafos son solo aquellos para categorías monoidales simétricas con algunos iconos adicionales, la definición es relativamente sencilla: solo queremos una estructura Frobenius en cada objeto. La única condición de coherencia es que estos interactúan muy bien con el producto monoidal.
Una categoría de hipergrafía es una categoría monoidal simétrica (C, I,) en la que cada objeto X está equipado con una estructura Frobenius (X, μ\(_{X}\), δ\(_{X}\), η\(_{X}\), ε\(_{X}\)) tal que
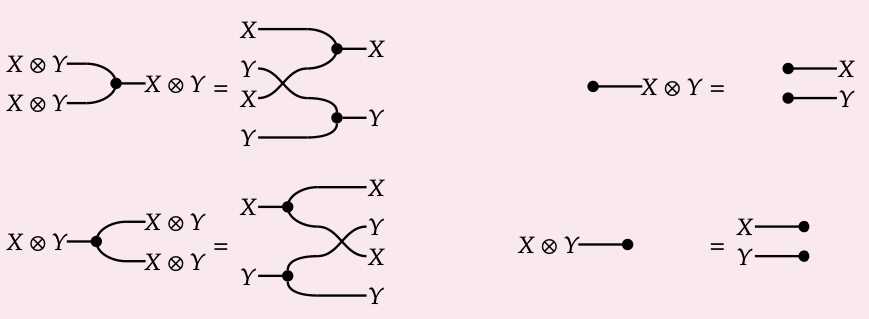
para todos los objetos X, Y, y tal que η\(_{I}\) = id\(_{I}\) = ε\(_{I}\).
Un prop de hipergrafía es una categoría de hipergrafía que también es un prop, por ejemplo, Ob (C) =\(\mathbb{N}\), etc.
Por Ejemplo 6.61, la categoría Cospan\(_{FinSet}\) es una categoría de hipergrafía. (De hecho, es equivalente a un hipergrafo prop.) Dibuja los morfismos Frobenius para el objeto 1 en Cospan\(_{FinSet}\) usando las representaciones de función y cableado como en el Ejemplo 6.46. ♦
Usando su conocimiento de los corlímites, demuestre que los mapas definidos en el Ejemplo 6.61 efectivamente obedecen a la ley especial (ver Definición 6.52) . ♦
Recordemos la categoría monoidal (Corel, Ø,) del Ejemplo 4.61; sus objetos son conjuntos finitos y sus morfismos son corelaciones.
Dado un conjunto finito X, definir la corelación μ\(_{X}\): X X → X tal que dos elementos de X X X sean equivalentes si y sólo si provienen del mismo elemento subyacente de X. Define δ\(_{X}\): X → X X de la misma manera, y defina η\(_{X}\): Ø → X y ε\(_{X}\): X → Ø tal que no haya dos elementos de X = Ø X = X Ø son equivalentes.
Estos mapas definen un monoide de Frobenius conmutativo especial (X, μ\(_{X}\), δ\(_{X}\), η\(_{X}\), ε\(_{X}\)), y de hecho le dan a Corel la estructura de una categoría de hipergrafía.
El apuntalamiento de las relaciones lineales, que mencionamos brevemente en el Ejercicio 5.84, es una categoría de hipergrafía. De hecho, se trata de una categoría de hipergrafía de dos maneras, eligiendo ya sea los generadores negros de 'copia' y 'descarte' o los generadores blancos de 'add' y 'cero' como los mapas de Frobenius.
Podemos generalizar la construcción que dimos en Teorema 5.87.
Las categorías de hipergrafía son categorías cerradas compactas autoduales, si definimos la copa y la tapa para ser
Comprobante. La prueba es una aplicación directa de los axiomas Frobenius y de unidad:
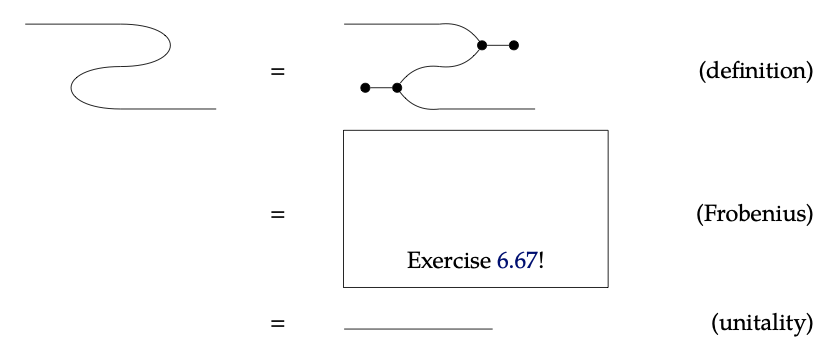\(\square\)
Rellene el diagrama faltante en la prueba de la Proposición 6.66 usando las ecuaciones de la Ec. (6.51), sus opuestos y la Ec. (6.53) . ♦