6.4: Cospanes decorados

Última actualización
Guardar como PDF

Page ID: 112208

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El objetivo de esta sección es mostrar cómo podemos construir una categoría de hipergrafía cuyos morfismos son circuitos eléctricos. Para ello, primero debemos introducir la noción de mapa conservador de estructura para categorías monoidales simétricas, una generalización de monótonos monoidales conocidos como funtores monoidales simétricos. Luego introducimos un método general el de cospanes decorados para producir categorías de hipergrafía. Hacer todo esto amarrará muchos cabos sueltos: colímites, cospanes, circuitos y categorías de hipergrafos.

Functores monoidales simétricos

Definición aproximada 6.68.

Que (C, I$_{C}$,$_{C}$) y (D$_{D}$, I,$_{D}$) sean cataciones monoidales simétricas. Para especificar un funtor monoidal simétrico (F, φ) entre ellos,

i) se especifica un funtor F: C → D;

(ii) se especifica un morfismo φ$_{I}$: I$_{D}$ → F (I$_{C}$).

(iii) por cada c$_{1}$, c$_{2}$$\in$ Ob (C), se especifica un morfismo

φ$_{c1,c2}$: F (c$_{1}$)$_{D}$ F (c$_{2}$) → F ($_{1}$c$_{C}$ c$_{2}$),

natural en c$_{1}$ y$_{2}$ c.

Llamamos a los diversos mapas φ mapas de coherencia.

Requerimos que los mapas de coherencia obedezcan axiomas contables que aseguren que se comporten bien con respecto a las estructuras monoidales simétricas en C y D. Si φ$_{I}$ y φ$_{c1,c2}$ son isomorfismos para todos c$_{1}$$_{2}$, c, decimos que ( F, φ) es fuerte.

Ejemplo 6.69.

Considere el functor de conjunto de potencia P: Set → Set. Actúa sobre los objetos enviando un conjunto S$\in$ Set a su conjunto de subconjuntos P (S) := {R$\subseteq$ S}. Actúa sobre morfismos enviando una función f: S → T al mapa de imagen im f: P (S) → P (T), que mapea R$\subseteq$ S a {f (r) | r $\in$R}$\subseteq$ T.

Ahora considere la estructura monoidal simétrica ({1}, ×) en Conjunto del Ejemplo 4.49. Para hacer de P un functor monoidal simétrico, necesitamos especificar una función φ$_{I}$: {1} → P ({1}) y para todos los conjuntos S y T, un functor φ$_{S,T}$: P (S) × P (T) → P (S × T). Una posibilidad es definir φ$_{I}$ (1) para que sea el subconjunto máximo {1}$\subseteq$ {1}, y dados los subconjuntos A$\subseteq$ S y B$\subseteq$ T, para definir φ$_{S,T}$ (A, B) como el subconjunto de productos A × B$\subseteq$ S × T. Con estas definiciones, (P, φ) es un funtor monoidal simétrico.

Ejercicio 6.70.

Comprobar que los mapas φ$_{S,T}$ definidos en el Ejemplo 6.69 son naturales en S y T. En otras palabras, dado f: S → S ′ y g: T → T ′, muestran que el siguiente diagrama conmuta:

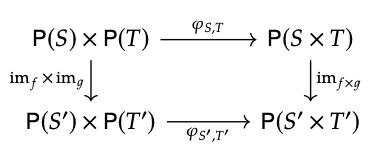$Screen Shot 2021-01-24 a las 5.41.09 PM.png$ ♦

Cospanes decorados

Ahora que hemos introducido brevemente los funtores monoidales simétricos, volvemos a la tarea que nos ocupa: construir una categoría de circuitos de hipergrafía. Para ello, se introduce el método de los cospanes decorados.

Los circuitos tienen mucha estructura interna, pero también tienen algunos puertos externos también llamados 'terminales' por los que interconectarlos con otros. Los cospanes decorados son formas de discutir exactamente eso: cosas con puertos externos y estructura interna.

Para ver cómo funciona esto, comencemos con el siguiente circuito de ejemplo:

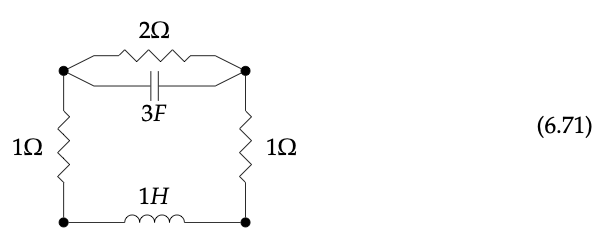
$Screen Shot 2021-01-24 a las 5.42.16 PM.png$

Podríamos considerar formalmente esto como un gráfico en el conjunto de cuatro puertos, donde cada borde está etiquetado por un tipo de componente de circuito (por ejemplo, el borde superior estaría etiquetado como una resistencia de resistencia 2Ω). Para que este circuito sea un morfismo en alguna categoría, es decir, para permitir la interconexión, debemos equipar al circuito con alguna noción de interfaz. Hacemos esto marcando los puertos en la interfaz usando funciones de conjuntos finitos:

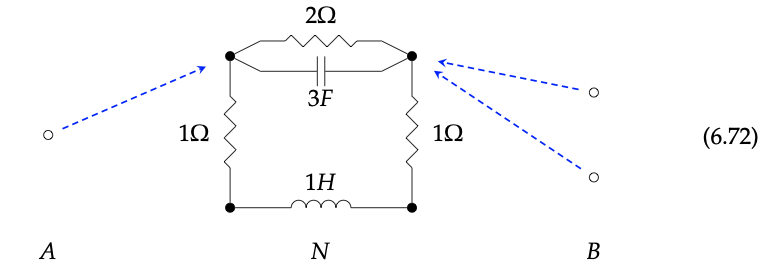
$Screen Shot 2021-01-24 a las 5.47.02 PM.png$

Sea N el conjunto de nodos del circuito. Aquí los conjuntos finitos A, B y N son conjuntos que constan de uno, dos y cuatro elementos respectivamente, dibujados como puntos, y los valores de las funciones A → N y B → N se indican con las flechas grises. Esto forma un cospan en la categoría de conjuntos finitos, para lo cual el conjunto de ápices N ha sido decorado por nuestro circuito dado.

Supongamos dado otro cospan decorado con entrada B

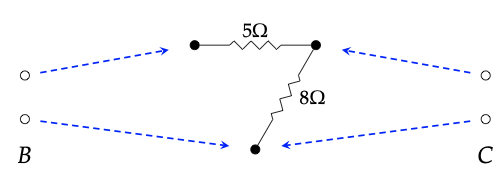
$Screen Shot 2021-01-24 a las 5.47.28 PM.png$

Dado que la salida del primero es igual a la entrada de la segunda (ambas son B), podemos pegarlas juntas en un solo diagrama:

$Screen Shot 2021-01-24 a las 5.48.12 PM.png$

La composición se da pegando los circuitos a lo largo de las identificaciones especificadas por B, dando como resultado el cospan decorado

$Screen Shot 2021-01-24 a las 5.48.39 PM.png$

Hemos visto este tipo de encolado antes cuando definimos la composición de cospanes en la Definición 6.45. Pero ahora está todo esto de la 'decoración'; nuestro objetivo es formalizarlo.

Definición 6.75.

Sea C una categoría con corlímites finitos, y (F, φ): (C, +) → (Set, ×) sea un funtor monoidal simétrico. Un cospan decorado en F es un par que consiste en un cospan$A \stackrel{i}{\rightarrow} N \stackrel{o}{\leftarrow} B$ en C junto con un elemento s ∈ F (N) .5 Llamamos (F, φ) el functor de decoración y s la decoración.

La intuición aquí es usar C = finSet, y, para cada objeto N$\in$ finSet, el functor F asigna el conjunto de todas las decoraciones legales en un conjunto N de nodos. Cuando eliges un cospan decorado con F, eliges un conjunto A de puertos externos izquierdos, un conjunto B de puertos externos a la derecha, cada uno de los cuales se asigna a un conjunto N de nodos, y eliges una de las decoraciones disponibles en N nodos, tomada de la juego F (N).

Entonces, en nuestra caja de circuito eléctrico, el functor de decoración F envía un conjunto finito N al conjunto de gráficos de diagramas de circuitos cuyos bordes están etiquetados por resistencias, capacitores, etc.—que tienen N vértices. Nuestro objetivo sigue siendo poder componer tales diagramas; entonces, ¿cómo funciona eso exactamente?

Básicamente se combina la forma en que se componen los cospanes con las estructuras que definen nuestro functor de decoración: a saber, F y φ.

Que ($A \stackrel{f}{\rightarrow} N \stackrel{g}{\leftarrow} B$, s) y ($B \stackrel{h}{\rightarrow} P \stackrel{k}{\leftarrow} C$, t) representen cospans decorados. Su compuesto está representado por el compuesto del cospan$A \stackrel{f}{\rightarrow} N \stackrel{g}{\leftarrow} B$ y$B \stackrel{h}{\rightarrow} P \stackrel{k}{\leftarrow} C$, emparejado con el siguiente elemento de F (N +$_{B}$ P):

$F\left(\left[\iota_{N}, \iota_{P}\right]\right)\left(\varphi_{N, P}(s, t)\right)$(6.76)

¡Eso es bastante compacto! Lo desempacaremos, en una caja concreta, en apenas un segundo. Pero primero grabemos un teorema.

Teorema 6.77.

Dada una categoría C con corlímites finitos y functor monoidal asimétrico (F, φ): (C, +) → (Set, ×), existe una categoría de hipergrafía Cospan$_{F}$ cuyos objetos son los objetos de C, y cuyos morfismos son clases de equivalencia de cospanes decorados en F.

Las estructuras simétricas monoidales e hipergráficas se derivan de las de Cospan$_{C}$.

Ejercicio 6.78.

Supongamos que le preocupa que la notación Cospan$_{C}$ se parezca a la notación Cospan$_{F}$, a pesar de que son muy diferentes. Un experto te dice “no son tan diferentes; uno es un caso especial del otro. Simplemente use el functor constante F (c) := {∗}.” ¿Qué significa el experto?

Circuitos eléctricos

Para trabajar con las abstracciones anteriores, obtendremos un poco más precisos sobre el ejemplo de los circuitos y luego veremos detalladamente cómo funciona la composición en categorías de cospan decoradas.

Construyamos algunos circuitos. Para comenzar, tendremos que elegir qué componentes queremos en nuestro circuito. Esto es simplemente una cuestión de lo que hay en nuestra caja de herramientas eléctricas. Digamos que llevamos algunas bombillas, interruptores, baterías y resistencias de todas las resistencias posibles. Es decir, definir un conjunto

$C:=\{\text { light, switch, battery }\} \sqcup\left\{x \Omega \mid x \in \mathbb{R}^{+}\right\}$

Para ser claros, los Ω son solo etiquetas; el conjunto anterior es isomórfico a {luz, interruptor, batería}$\mathbb{R}$ +. Pero escribimos C de esta manera para recordarnos que consiste en componentes de circuito. Si quisiéramos, también podríamos agregar inductores, capacitores e incluso elementos que conecten más de dos puertos, como transistores, pero mantengamos las cosas simples por ahora.

Dado nuestro conjunto C, un circuito C es solo una gráfica (V, A, s, t), donde s, t: A → V son las funciones fuente y destino, junto con una función l: A → C etiquetando cada borde con un cierto componente de circuito de C.

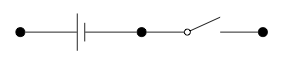
Por ejemplo, podríamos tener el caso simple de V = {1,2}, A = {e}, s (e) = 1, t (e) = 2 así que e es un borde de 1 a 2 y l (e) = 3Ω. Esto representa una resistencia con resistencia 3Ω:

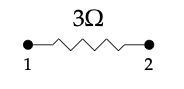
$Screen Shot 2021-01-24 at 6.16.51 PM.png$

Tenga en cuenta que en el formalismo que hemos elegido, tenemos múltiples formas de representar cualquier circuito, ya que nuestras representaciones eligen explícitamente direcciones para los bordes. La resistencia anterior también podría estar representada por el 'gráfico inverso', con los datos V = {1, 2}, A = {e}, s (e) = 2, t (e) = 1, y l (e) = 3 F.

Ejercicio 6.79.

Escribe una tupla (V, A, s, t, l) que represente el circuito en la Ec. (6.71) . ♦

Un functor de decoración para circuitos. Queremos que los circuitos C sean nuestras decoraciones, así que usémoslos para definir un functor de decoración como en la Definición 6.75.

Llamaremos al functor (Circ, ψ). Comenzamos definiendo la parte functor

Circ: (FinSet, +) → (Set, ×)

como se indica a continuación. En los objetos, simplemente envíe un conjunto finito V al conjunto de circuitos C:

Circ (V) := {(V, A, s, t, l) | donde s, t: A → V, l: E → C}.

En morfismos, Circ envía una función f: V → V ′ a la función

Circ (f): Circ (V) → Circ (V ′);

(V, A, s, t, l)$\longmapsto$ (V', A, (s; f), (t; f), l).

Esto define a un functor; vamos a explorarlo un poco en un ejercicio.

Ejercicio 6.80.

Para entender mejor este functor, que c$\in$ Circ ($\underline{4}$) sea el circuito

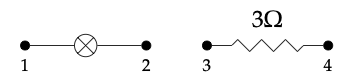
$Screen Shot 2021-01-24 a las 6.35.35 PM.png$

y deja que f:$\underline{4}$ →$\underline{3}$ sea la función

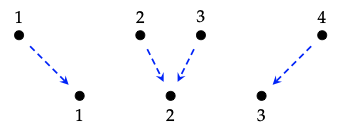
$Screen Shot 2021-01-24 a las 6.36.50 PM.png$

Dibuja una imagen del circuito Circ (f) (c) . ♦

Estamos tratando de conseguir un functor de decoración (Circ, ψ) y hasta ahora tenemos Circ. Para los mapas de coherencia ψ$_{V,V'}$ para conjuntos finitos V, V′, definimos

\ (\ begin {array} {c}
\ psi_ {V, V^ {\ prime}}:\ nombreoperador {Circ} (V)\ veces\ nombreoperador {Circ}\ izquierda (V^ {\ prime}\ derecha)\ largofila derecha\ nombreoperador {Circ}\ izquierda (V+V^ {\ prime}\ derecha)\
\ izquierda ((V, A, s, t,\ ell),\ left (V^ {\ prime}, A^ {\ prime}, s^ {\ prime}, t^ {\ prime},\ ell^ {\ prime}\ derecha)\ derecha) \ longmapsto\ izquierda (V+V^ {\ prime}, A+A^ {\ prime}, s+s^ {\ prime}, t+t^ {\ prime},\ izquierda [\ ell,\ ell^ {\ prime}\ derecha]\ derecha)
\ end {array}\) (6.81)

Esto es más sencillo de lo que podría parecer: toma un circuito en V y un circuito en V ′, y solo los considera juntos como un circuito en la unión disjunta de vértices V + V′.

Ejercicio 6.82.

Supongamos que tenemos circuitos

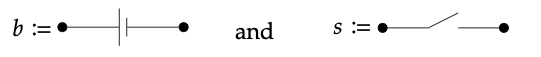
$Screen Shot 2021-01-24 a las 6.40.05 PM.png$

en Circ ($\underline{2}$).

Use la definición de ψ$_{V,V'}$ de (6.81) para averiguar qué circuito de 4 vértices ψ$_{\underline{2},\underline{2}}$ (b, s)$\in$ Circ ($\underline{2}$+$\underline{2}$) = Circ ($\underline{4}$) debería ser, y dibujar una imagen. ♦

Circuitos abiertos utilizando cospanes decorados. A partir de los datos anteriores, solo un functor monoidal (Circ, ψ): (FinSet, +) → (Set, ×), ¡podemos construir nuestra prometida categoría de hipergrafía de circuitos!

Nuestra notación para esta categoría es Cospan$_{Circ}$. Siguiendo el Teorema 6.77, los objetos de esta categoría son los mismos que los objetos de FinSet, solo conjuntos finitos. Retomaremos nuestra notación a partir de la introducción y el Ejemplo 6.42, y dibujaremos estos conjuntos finitos como colecciones de círculos blancos ◦.

Por ejemplo, representaremos el objeto 2 de Cospan$_{Circ}$ como dos círculos blancos:

$Screen Shot 2021-01-24 at 6.43.58 PM.png$

Estos círculos blancos marcan puntos de interfaz de un circuito abierto.
Más interesantes que los objetos, sin embargo, son los morfismos en Cospan$_{Circ}$.

Se trata de circuitos abiertos. Por Teorema 6.77, un morfismo$\underline{m}$ →$\underline{n}$ es un cospan decorado con Circ: es decir, cospan$\underline{m}$ →$\underline{p}$ ←$\underline{n}$ junto con un elemento c de Circ ($\underline{p}$).

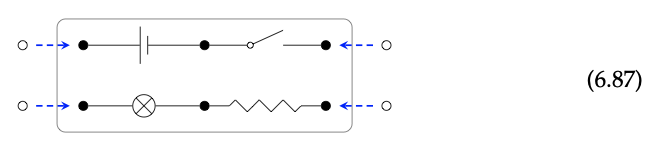
Como ejemplo, considere el cospan$\underline{1} \stackrel{i_{1}}{\rightarrow} \underline{2} \stackrel{i_{2}}{\leftarrow} \underline{1}$ donde i$_{1}$ (1) = 1 e i$_{2}$ (1) = 2, equipado con el elemento de batería de Circ ($\underline{2}$) conectando el nodo 1 y el nodo 2. Describiremos esto de la siguiente manera:

$Screen Shot 2021-01-24 at 6.51.02 PM.png$

Ejercicio 6.84.

Los morfismos de Cospan$_{Circ}$ son cospanes decorados con Circ, tal como se definen en la Definición 6.75. Este medio (6.83) representa un cospan junto con una decoración, que es algún circuito C (V, A, s, t, l)$\in$ Circ ($\underline{2}$). ¿Qué es? ♦

Veamos ahora cómo se$_{Circ}$ pueden utilizar las operaciones de hipergrafía en Cospan para construir circuitos eléctricos.

Composición en Cospan$_{Circ}$. Primero consideraremos la composición. Considere el siguiente cospan decorado de$\underline{1}$ a$\underline{1}$:

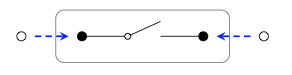
$Screen Shot 2021-01-24 at 6.54.47 PM.png$

Dado que este y el circuito en (6.83) son ambos morfismos$\underline{1}$ →$\underline{1}$, podemos componerlos para obtener otro morfismo$\underline{1}$ →$\underline{1}$. ¿Cómo hacemos esto? Hay dos partes: para obtener el nuevo cospan, simplemente componemos los cospanes de nuestros dos circuitos, y para obtener la nueva decoración, utilizamos la fórmula Circ ([ι$_{N}$, ι$_{P}$]) (ψ$_{N,P}$ (s, t)) a partir de (6.76). De nuevo, ¡esto es bastante compacto! Vamos a desempacarlo juntos.

Empezaremos con los cospanes. Los cospans que deseamos componer son

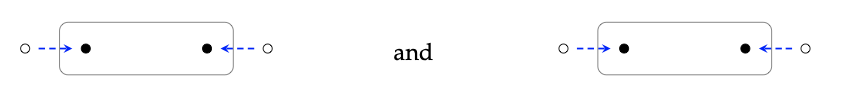
$Screen Shot 2021-01-24 at 6.59.26 PM.png$

Simplemente ignoramos las decoraciones por ahora.) Si hacemos pushout sobre el conjunto común 1 = {◦}, obtenemos el cuadrado pushout

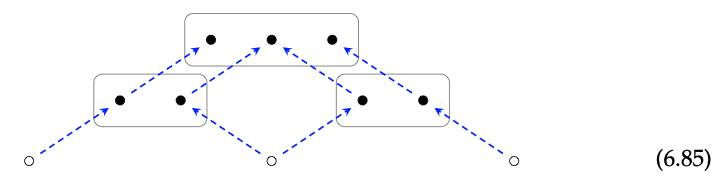
$Screen Shot 2021-01-24 a las 7.00.08 PM.png$

Esto significa que el cospan compuesto es

$Screen Shot 2021-01-24 en 7.04.43 PM.png$

Mientras tanto, ya te teníamos que empezar desempacando la fórmula para la nueva decoración. Nos dijiste lo que$_{\underline{2},\underline{2}}$ hace el mapa ψ en el Ejercicio 6.82. Toma las dos decoraciones, ambos circuitos en Circ ($\underline{2}$), y las convierte en el circuito único y disjunta

$Screen Shot 2021-01-24 a las 7.13.30 PM.png$

en Circ ($\underline{4}$). Entonces esto es lo que significa la parte ψ$_{N,P}$ (s, t). ¿Qué significa the [ι$_{N}$, ι$_{P}$]? Recordemos que este es el copaireo de los mapas pushout, como se describe en los Ejemplos 6.14 y 6.25. En nuestro caso, el cuadrado de pushout relevante viene dado por (6.85), y [ι$_{N}$, ι$_{P}$] es de hecho la función f del Ejercicio 6.80!

Esto significa que la decoración en el cospan compuesto es

$Screen Shot 2021-01-24 a las 7.13.56 PM.png$

Poniendo todo esto junto, el circuito compuesto es

$Screen Shot 2021-01-24 a las 7.18.48 PM.png$

Ejercicio 6.86.

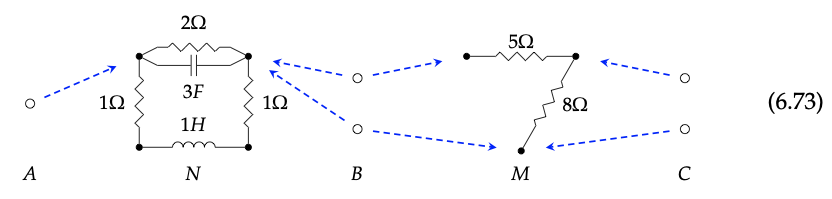
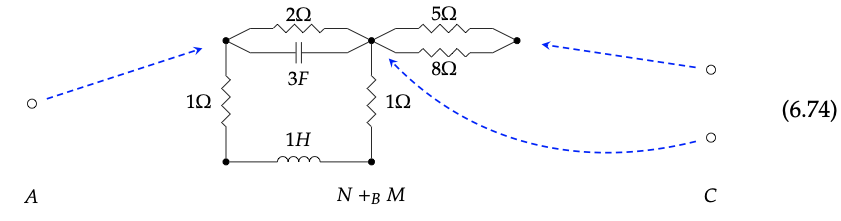
Refiérase al ejemplo al inicio de la Sección 6.4.2. En particular, considere la composición de los circuitos en la Ec. (6.73). Expresar los dos circuitos en este diagrama como morfismos en Cospan$_{Circ}$, y computar su compuesto. ¿Coincide con la imagen en la Ec. (6.74)? ♦

Productos monoidales en Cospan$_{Circ}$. Los productos monoidales en Cospan$_{Circ}$ son mucho sim- pler que composición. En los objetos, nuevamente simplemente trabajamos como en FinSet: tomamos la unión disjunta de conjuntos finitos. Los morfismos vuelven a tener un cospan, y una decoración.

Para los cospanes, nuevamente solo trabajamos en Cospan$_{FinSet}$: dados dos cospanes A → M ← B y C → N ← D, tomamos su cospan de coproducto A + C → M + N ← B + D. Y para decoraciones, utilizamos el mapa ψ$_{M,N}$: Circ (M) × Circ (N) → Circ (M + N). Entonces, por ejemplo, supongamos que queremos tomar el producto monoidal de los circuitos abiertos

$Screen Shot 2021-01-24 a las 7.22.09 PM.png$

$Screen Shot 2021-01-24 a las 7.24.40 PM.png$

El resultado viene dado apilándolos. En otras palabras, su producto monoidal es:

$Screen Shot 2021-01-24 a las 7.24.45 PM.png$

Fácil, ¿verdad?

Te dejamos hacer dos composiciones propias.

Ejercicio 6.88.

Escribe x para el circuito abierto en (6.87). Definir también cospans η: 0 → 2 y η: 2 → 0 de la siguiente manera:

$Screen Shot 2021-01-24 a las 7.24.50 PM.png$

donde cada uno de estos son decorados por el circuito vacío (1, Ø,! ,! ,!) $\in$Circ ($\underline{1}$). $^{6}$

Calcular el compuesto η; x; ε en Cospan$_{Circ}$. Esto es un morfismo$\underline{0}$ →$\underline{0}$; llamamos a tales cosas circuitos cerrados. ♦