6.5: Óperas y sus álgebras

En el Teorema 6.77 describimos cómo decorar cospanes construye una categoría de hipergrafía a partir de un funtor monoidal simétrico. Luego exploramos cómo funciona eso en el caso de que el functor de decoración sea de alguna manera “todas las gráficas de circuito en un conjunto de nodos”.

En este libro, hemos dedicado mucha atención a diferentes tipos de teorías compositivas, desde preordenes monoidales hasta categorías cerradas compactas y categorías hipergráficas. Sin embargo, para una aplicación que algún día tienes en mente, puede darse el caso de que ninguna de estas teorías sea suficiente. Se necesita una estructura diferente, personalizada a una situación particular. Por ejemplo en [VSL15] los autores quisieron componer sistemas dinámicos continuos con propiedades teóricas de control y se dieron cuenta de que para que la retroalimentación tuviera sentido, los diagramas de cableado no podían involucrar lo que llamaban 'cables pasados'.

Entonces, para cerrar nuestra discusión sobre las estructuras compositivas, queremos esbozar rápidamente algo que podamos usar como una especie de estructura metacomposicional, conocida como operada. Vimos en la Sección 6.4.3 que podemos construir circuitos eléctricos a partir de un functor monoidal simétrico FinSet → Set. Del mismo modo veremos que podemos construir ejemplos de nuevas estructuras algebraicas a partir de los funcionadores de operadas O → Set.

Diagramas de diseño de cableado

Comprender que los circuitos son morfismos en una categoría de hipergrafía es útil: significa que podemos poner en práctica la maquinaria de la teoría de categorías en la comprensión de los circuitos eléctricos. Por ejemplo, podemos construir funtores que expresen la composicionalidad de la semántica de circuitos, es decir, cómo derivar la funcionalidad del conjunto a partir de la funcionalidad y el patrón de interacción de las partes. O podemos usar la base teórica de categoría para relacionar circuitos con otros tipos de sistemas de red, como los gráficos de flujo de señal. Finalmente, los teoremas básicos de coherencia para categorías monoidales y categorías cerradas compactas nos dicen que los diagramas de cableado dan un razonamiento sólido y completo en estos escenarios.

Sin embargo, un resultado quizás insatisfactorio es que la categoría de hipergrafía introduce artefactos como el dominio y el codominio de un circuito, que no son inherentes a la estructura de los circuitos ni a su composición. Los circuitos solo tienen una interfaz de límite única, no 'dominios' y 'codominios'. Esto no quiere decir que el modelo anterior no sea útil: en muchas aplicaciones, un espacio vectorial no tiene una base preferida, pero a menudo es útil elegir uno para que podamos usar matrices (¡o gráficas de flujo de señal!). Pero valdría la pena contar con un modelo teórico-categórico que represente de manera más directa la estructura compositiva de los circuitos. En general, queremos que el modelo teórico de categoría se ajuste a nuestra aplicación deseada como un guante. Vamos a bosquejar rápidamente cómo se puede hacer esto.

Volvamos a los diagramas de cableado por un segundo. Vimos que los diagramas de cableado para categorías de hipergrafos básicamente se ven así:

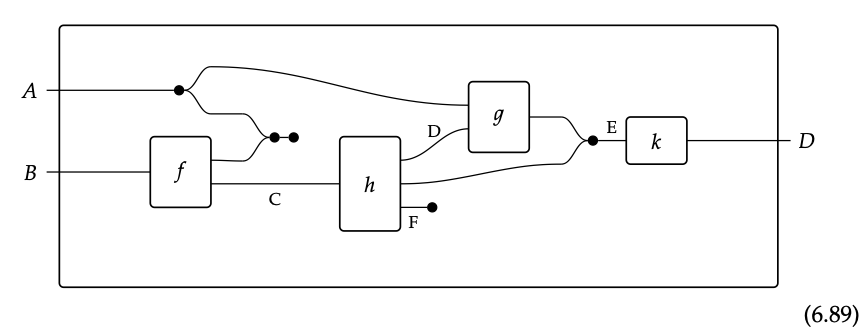
Tenga en cuenta que si tuviera una caja con A y B a la izquierda y D a la derecha, podría enchufar el diagrama anterior justo dentro de él, y obtener un nuevo circuito abierto. Este es el movimiento básico de las óperas.

Pero antes de explicar esto, vamos a llegar a donde dijimos que queríamos ir: a un modelo donde no hay puertos a la izquierda y puertos a la derecha, solo hay puertos. Queremos un modelo de composición más sucinto para diagramas de circuitos; algo que se vea más así:

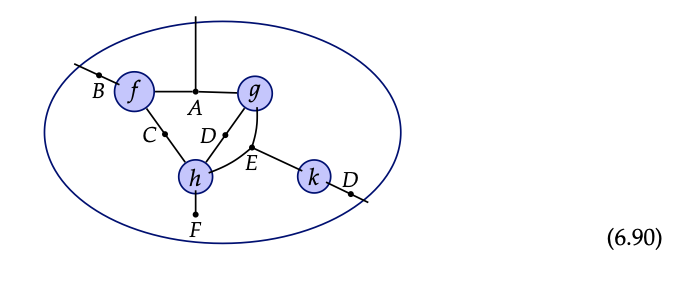
¿Ves como los diagramas Eq. (6.89) y Eq. (6.90) son en realidad exactamente los mismos en

términos de patrón de interconexión? La única diferencia es que este último no tiene distinción de izquierda/derecha: hemos perdido exactamente lo que queríamos perder.

El costo es que las 'cajas' f, g, h, k en la Ec. (6.90) ya no tienen una disección izquierda/derecha; ahora solo son círculos. Eso no estaría mal excepto que significa que ya no pueden representar morfismos en una categoría —como solían hacerlo anteriormente, en la Ec. (6.89) porque los morfismos en una categoría por definición tienen un dominio y un codominio. Nuestros nuevos círculos no tienen tal distinción. Entonces ahora necesitamos una forma completamente nueva de pensar categóricamente las 'cajas': si ya no son morfismos en una categoría, ¿qué son? La respuesta se encuentra en la teoría de las óperas.

Al entender las óperas, encontraremos que necesitamos navegar por uno de los cambios de nivel que primero discutimos en la Sección 1.4.5. Observe que para los cospanes decorados, definimos una categoría de hipergrafía utilizando un functor monoidal simétrico. Esto es una reminiscencia de nuestra breve discusión sobre las teorías algebraicas en la Sección 5.4.2, donde definimos algo llamado la teoría de los monoides como un prop M, y definimos monoides usando los funtores M → Conjunto; ver Observación 5.74.

De la misma manera, podemos ver la categoría Cospan\(_{FinSet}\) como una especie de 'teoría de las categorías de hipergrafía', y así definir categorías de hipergrafía como funtores Cospan\(_{FinSet}\) → Set.

Entonces esa es la idea. Una operada O definirá una teoría o gramática de la composición, y los funcionadores de operada O → Conjunto, conocidos como O-álgebras, describirán aplicaciones particulares que obedecen a esa gramática.

Definición aproximada 6.91.

Para especificar una operada O,

i) se especifica una colección T, cuyos elementos se denominan tipos;

(ii) para cada tupla (t\(_{1}\),..., t\(_{n}\), t) de tipos, se especifica un conjunto O (t\(_{1}\),..., t\(_{n}\); t), cuyos elementos se denominan operaciones de arity (t\(_{1}\),..,.,., t\(_{n}\); t);

(iii) por cada par de tuplas (s\(_{1}\),..., s\(_{m}\), t\(_{i}\)) y (t\(_{1}\),..., t\(_{n}\), t), se especifica una función

◦\(_{i}\): O (s\(_{1}\),..., s\(_{m}\); t\(_{i}\)) × O (t\(_{1}\),..., t\(_{n}\); t) → O (t\(_{1}\),..., t\(_{i-1}\), s\(_{1}\),..., s \(_{m}\), t\(_{i+1}\),..., t\(_{n}\); t);

llamada sustitución; y

(iv) para cada tipo t, se especifica una operación id\(_{t}\) \(\in\)O (t; t) llamada operación de identidad.

Estos deben obedecer las leyes generalizadas de identidad y asociatividad.

Ignoremos los tipos por un momento y pensemos en lo que modela esta estructura. La intuición es que una operada consiste en, por cada n, un conjunto de operaciones de arity n es decir, todas las operaciones que aceptan n argumentos. Si tomamos una operación f de arity m, y enchufamos la salida al argumento i ésimo de una operación g de arity n, deberíamos obtener una operación de arity m + n − 1: tenemos m argumentos para rellenar m, y los restantes n − 1 argumentos para rellenar m. ¿Qué operación de arity m + n − 1 obtenemos? Esto es descrito por la función de sustitución ◦\(_{i}\), que dice que obtenemos la operación f ◦\(_{i}\) g\(\in\) O (m + n − 1). Las condiciones de coherencia dicen que estas funciones ◦\(_{i}\) capturan la siguiente imagen intuitiva:

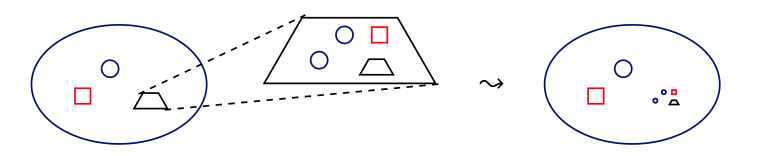
Los tipos entonces nos permiten especificar los, bueno, tipos de las entradas de argumentos que toma cada función. Por lo que hacer té es una operación 2-aria, una operación con arity 2, porque toma en dos cosas. Para hacer té necesitas un poco de agua tibia, y necesitas algunas hojas de té.

Ejemplo 6.92.

Las gramáticas libres de contexto son para óperas como gráficas para categorías. Vamos a bosquejar lo que esto significa. Primero, una gramática libre de contexto es una manera de describir un conjunto particular de 'categorías sintácticas' que se pueden formar a partir de un conjunto de símbolos. Por ejemplo, en inglés tenemos categorías sintácticas como sustantivos, determinantes, adjetivos, verbos, frases sustantivas, frases preposicionales, oraciones, etc. Los símbolos son palabras, por ejemplo gato, perro, the, persecuciones.

Para definir una gramática libre de contexto en algún alfabeto, se especifican algunas reglas de producción, que dicen cómo formar una entidad en alguna categoría sintáctica a partir de un grupo de entidades en otras categorías sintácticas. Por ejemplo, podemos formar una frase sustantiva a partir de un determinador (el), un adjetivo (feliz), y un sustantivo (niño). Las gramáticas libres de contexto son importantes tanto en la lingüística como en la informática. En los primeros, son una forma básica de hablar sobre la estructura de las oraciones en lenguajes naturales. En estos últimos, son cruciales a la hora de diseñar analizadores para lenguajes de programación.

Así que al igual que las gráficas presentan categorías gratuitas, las gramáticas libres de contexto presentan óperas gratuitas. Esta idea se notó por primera vez en [HMP98].

Óperas de categorías monoidales simétricas

Veremos en la Definición 6.97 que una gran clase de óperas provienen de categorías monoidales simétricas. Antes de explicar esto, damos un par de ejemplos. Quizás la operada más importante es la de Set.

Ejemplo 6.93.

La operada Conjunto de conjuntos tiene

(i) Establece X como tipos.

(ii) Funciones X\(_{1}\) × ··· × X\(_{n}\) → Y como operaciones de arity (X\(_{1}\),..., X\(_{n}\); Y).

iii) Sustitución definida por

(g ◦\(_{i}\) f) (x\(_{1}\),..., x\(_{i-1}\), w\(_{1}\),..., w\(_{m}\), x\(_{i+1}\),..., x\(_{n}\))
= g ( x\(_{1}\),..., x\(_{i-1}\), f (w\(_{1}\),..., w\(_{m}\)), x\(_{i+1}\),..., x\(_{n}\)

donde f\(\in\) Conjunto (W\(_{1}\),..., W\(_{m}\); X\(_{i}\)), g\(\in\) Conjunto (X\(_{1}\),..., X\(_{n}\); Y), y por lo tanto g ◦ \(_{i}\)f es una función

(g ◦\(_{i}\) f): X\(_{1}\) × ··· × X\(_{i-1}\) × W\(_{1}\) × ··· × W\(_{m}\) × X\(_{i+1}\) × ··· × X\(_{n}\) → Y

(iv) Identidades id\(_{X}\) \(\in\)Set (X; X) vienen dadas por la función de identidad id\(_{X}\): X → X.

A continuación damos un ejemplo que nos recuerda para qué eran todas estas cosas de la operada: diagramas de cableado.

Ejemplo 6.94.

La operada Cospan de cospans de conjunto finito tiene

(i) Números naturales a\(\in\)\(\mathbb{N}\) como tipos.

(ii) Cospanes a\(\underline{_{1}}\) + ··· + a\(\underline{_{n}}\) → p ← b de conjuntos finitos como operaciones de arity (a\(_{1}\),..., a\(_{n}\); b).

iii) Sustitución definida por pushout.

(iv) Identidades id\(_{a}\) \(\in\)Set (a; a) que acaba de dar el cospan de identidad\(\underline{a}\)\ stackrel\(_{\underline{a}}\) {id {\ rightarrow}\(\underline{a}\)\ stackrel {id\(_{\underline{a}}\)} {\ leftarrow}\(\underline{a}\)\).

Este es el análogo operádico de la categoría monoidal (Cospan\(_{FinSet}\), 0, +).

Podemos representar operaciones en esta operada usando diagramas como los que dibujamos arriba. Por ejemplo, aquí hay una imagen de una operación:

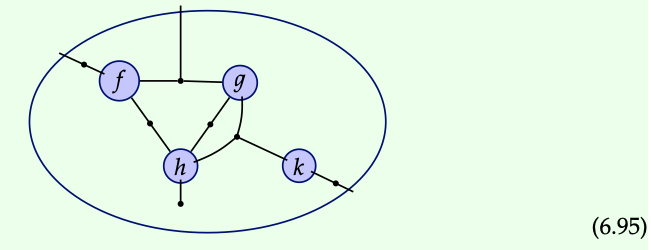
Se trata de una operación de arity (\(\underline{3}\),\(\underline{3}\),\(\underline{4}\),\(\underline{2}\); 3). ¿Por qué? Los círculos marcados con f y g tienen 3 puertos, h tiene 4 puertos, k tiene 2 puertos, y el círculo exterior tiene 3 puertos: 3, 3, 4, 2; 3.

Entonces, ¿cómo es exactamente la ecuación (6.95) un morfismo en esta operada?

Bueno un morfismo de este\(\underline{3}\) +\(\underline{3}\)\(\underline{4}\) +\(\underline{2}\)\ stackrel {a} {\ rightarrow}\ subrayado {p}\ stackrel {b} {\ leftarrow}\ subrayado {3}\).

En el diagrama anterior, el ápice\(\underline{p}\) es el conjunto\(\underline{7}\), pues hay 7 nodos • en el diagrama. La función a envía cada puerto en uno de los círculos pequeños al nodo al que se conecta, y la función b envía cada puerto del círculo exterior al nodo al que se conecta.

Somos capaces de representar cada operación en la operada Cospan como un diagrama de cableado. A menudo es útil pensar en las óperas como una descripción de la gramática de un diagrama de cableado. La operación de sustitución de la operada significa insertar un diagrama de cableado en un círculo o caja en otro diagrama de cableado.

Ejercicio 6.96.

1. Considere el siguiente cospan f\(\in\) Cospan (2, 2; 2):

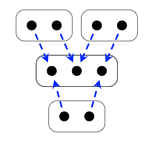
Dibujarlo como un diagrama de cableado con dos círculos internos, cada uno con dos puertos, y un círculo exterior con dos puertos.

2. Dibuje el diagrama de cableado correspondiente al siguiente cospan g\(\in\) Cospan (2, 2, 2; 0):

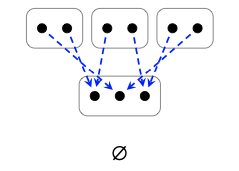
3. Calcular el cospan g ◦\(_{1}\) f. ¿Cuál es su aridad?

4. Dibuja el cospan g ◦\(_{1}\) f. ¿Lo ve como sustitución? ♦

Podemos convertir cualquier categoría monoidal simétrica en una operada de manera que genere los dos ejemplos anteriores.

Definición 6.97.

Para cualquier categoría monoidal simétrica (C, I,), existe una operada O\(_{C}\), llamada la operada subyacente C, definida como que tiene:

(i) Ob (C) como tipos.

(ii) morfismos \(_{1}\)C ··· C\(_{n}\) → D en C como las operaciones de arity (C\(_{1}\),..., C\(_{n}\); D).

(iii) la sustitución se define por

(f ◦\(_{i}\) g) := f ◦ (id,..., id, g, id,..., id)

(iv) identidades id\(_{a}\) \(\in\)O\(_{C}\) (a; a) definidas por id\(_{a}\).

También podemos convertir cualquier funtor monoidal en lo que se llama un functor de operada.

La operada para los apoyos de hipergrafía

Un funtor de operada toma los tipos de una operada a los tipos de otra, y luego las op- eraciones de la primera a las operaciones de la segunda de una manera que respete esto.

Rpugh Definición 6.98.

Supongamos dados dos óperas O y P con colecciones de tipo T y U respectivamente. Para especificar un funtor de operada F: O → P,

(i) uno especifica una función f: T → U.
(ii) Para todas las peculiaridades (t\(_{1}\),..., t\(_{n}\); t) en O, se especifica una función

F: O (t\(_{1}\),..., t\(_{n}\); t) → P (f (t\(_{1}\)),..., f (t\(_{n}\)); f (t))

de tal manera que se preserven la composición y las identidades.

Así como los funtores de valores establecidos C → Conjunto de cualquier categoría C son de particular interés, los vimos como instancias de base de datos en el Capítulo 3, así que son Functores de Valor Conjunto O → Establecer desde cualquier operada O.

Definición 6.99.

Un álgebra para una operada O es una operada functor F: O → Set.

Podemos pensar en los funtores O → Establecer como definir un conjunto de posibles formas de llenar las cajas en un diagrama de cableado. De hecho, cada caja en un diagrama de cableado representa un tipo t de la operada dada O y un álgebra F: O → Set tomará un tipo t y devolverá un conjunto F (t) de rellenos para la caja t. Además, dada una operación (es decir, un diagrama de cableado) f\(\in\) O (t 1,.., t n; t), obtenemos una función F (f) que toma un elemento de cada conjunto F (t i), y devuelve un elemento de F (t). Por ejemplo, toma n circuitos con interfaz t 1,.., t n respectivamente, y devuelve un circuito con límite t.

Ejemplo 6.100.

Para los circuitos eléctricos, los tipos son nuevamente conjuntos finitos, T = Ob (FinSet), donde cada conjunto finito \(\in\)t T corresponde a una celda con t puertos. Al igual que antes, tenemos un conjunto Circ (t) de rellenos, es decir, el conjunto de circuitos eléctricos con esos terminales marcados en t. Como álgebra de óperas, Circ: Cospan → Set transforma diagramas de cableado como este

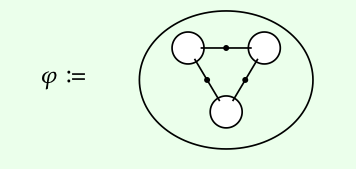
en fórmulas que construyen un nuevo circuito a partir de un montón de existentes.

En el caso dibujado arriba, obtendríamos un morfismo Circ (φ)\(\in\) Set (Circ (2), Circ (2), Circ (2); Circ (0)), es decir, una función

Circ (φ): Circ (2) × Circ (2) × Circ (2) → Circ (0).

Podríamos aplicar esta función a los tres elementos de Circ (2) mostrados aquí

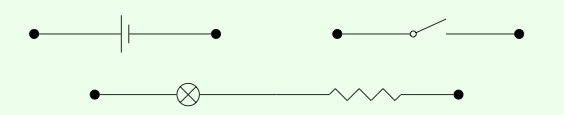
y el resultado sería el circuito cerrado desde el inicio del capítulo:

Esto es una reminiscencia de la historia de los cospanes decorados: pegar rellenos para formar categorías de hipergrafos. Una ventaja de la construcción de cospan decorada es que se obtiene una categoría explícita (donde los morfismos tienen dominios y codominios y por lo tanto se pueden componer asociativamente), equipada con estructuras Frobenius que nos permiten sortear las estenosis de dominios y codominios. La perspectiva de la operada tiene otras ventajas. Primero, mientras que los cospanes decorados pueden producir solo algunas categorías de hipergrafía, Cospan -álgebras pueden producir cualquier categoría de hipergrafía.

Proposición 6.101.

Existe una equivalencia entre Cospan -álgebras y apoyos hipergráficos.

Otra ventaja de usar óperas es que se puede variar la operada misma, de Cospan a algo similar (como la operada de 'cobordisms'), y obtener reglas de composicionalidad ligeramente diferentes.

De hecho, las operadas con la complejidad adicional en su definición, pueden ser cutomizadas incluso más que todas las estructuras composicionales definidas hasta ahora. Por ejemplo, podemos definir óperas de diagramas de cableado donde los diagramas de cableado deben obedecer condiciones precisas mucho más específicas que las restricciones de una categoría, como requerir que el diagrama en sí no tenga cables que pasen directamente a través de él. De hecho, las óperas son lo suficientemente fuertes como para definirse a sí mismas: en términos generales, hay una operada para las óperas: la categoría de óperas es equivalente a la categoría de álgebras para una determinada operada [Lei04, Ejemplo 2.2.23]. Si bien las óperas pueden, por supuesto, volver a generalizarse, concluyen nuestra marcha a través de una jerarquía informal de estructuras compositivas, desde preordenes hasta categorías hasta categorías monoidales y óperas.