8.3: Soluciones para el Capítulo 3
- Page ID
- 112245
Hay cinco columnas sin ID en la Ecuación (3.1) y cinco flechas en la Ecuación (3.2). Esto no es una coincidencia: siempre hay una flecha por cada columna que no sea ID.
Para hacer esto precisamente, debemos definir técnicamente la concatenación.
Si G = (V, A, s, t) es una gráfica, defina una ruta en G para que sea una tupla de la forma (v, a\(_{1}\),.,., a\(_{n}\)) donde v\(\in\) V es un vértice, s (a\(_{1}\)) = v, y t (a\(_{i}\)) = s (a\(_{i+1}\)) para todos i\(\in\) {1,.., n − 1}; la longitud de esta ruta es n, y esta definición hace sentido para cualquier n\(\in\)\(\mathbb{N}\). Decimos que la fuente de p es s (p) := v y el objetivo de p se define como
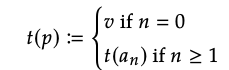
Dos caminos p = (v, a\(_{1}\),..., a\(_{m}\)) y q = (w, b\(_{1}\),..., b\(_{n}\)) se pueden concatenar si t (p) = s (q), en cuyo caso la ruta concatenada p; q se define como
(p; q) := (v, a\(_{1}\),.., a\(_{m}\), b\(_{1}\),..., b\(_{n}\)).
Ya estamos listos para verificar la unidad y la asociatividad. Una ruta p es una identidad en Libre (G) iff p = (v) para algunos \(\in\)v V.
Es fácil ver por lo anterior que (v) y (w, b,...\(_{1}\), b\(_{n}\)) se pueden concatenar iff v = w, en cuyo caso el resultado es (w, b\(_{1}\),..., b\(_{n}\)). De igual manera (v\(_{1}\), a,..., a\(_{m}\)) y (w) se pueden concatenar iff w = t (a\(_{m}\)), en cuyo caso el resultado es (v, a\(_{1}\),.,., a \(_{m}\)). Finalmente, para asociatividad con p y q como arriba y r = (x, c\(_{1}\),.., c o), la fórmula lee fácilmente que sea cual sea la forma en que estén concatenados, (p; q); r o p; (q; r), el resultado es
(v, a\(_{1}\),..., a\(_{m}\), b\(_{1}\),..., b\(_{n}\), c\(_{1}\),..., c\(_{o}\)).
A menudo nos gusta nombrar morfismos de identidad por los objetos en los que están, y lo hacemos aquí: v\(_{2}\) significa id\(_{v2}\). Escribimos ☒ cuando el compuesto no tiene sentido (es decir, cuando el objetivo del primer morfismo no concuerda con la fuente del segundo).

1. La categoría 1 tiene un objeto v\(_{1}\) y un morfismo, el id de identidad\(_{v1}\).
2. La categoría 0 está vacía; no tiene objetos y nomorfismos.
3. El patrón para número de morfismos en 0, 1, 2, 3 es 0, 1, 3, 6; ¿este patrón le resulta familiar? Estos son los primeros 'números triangulares', así que podríamos adivinar que el número de morfismos en n, la categoría libre en la siguiente gráfica
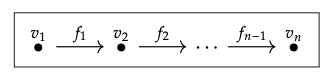
es 1 + 2 + · · · + n. Esto tiene sentido porque (y la estrategia de prueba sería verificar que) la gráfica anterior tiene n rutas de longitud 0, tiene n − 1 rutas de longitud 1, y así sucesivamente: tiene n − i rutas de longitud i por cada 0 ≤ i ≤ n.
La correspondencia se dio enviando un camino a su longitud.
Concatenar una trayectoria de longitud m con una trayectoria de longitud n da como resultado una trayectoria de longitud m + n.
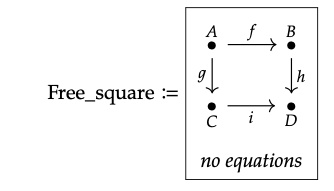
1. Los diez caminos son los siguientes
A, A; f, A; g, A; f; h, A; g; i, B, B; h , C, C; i, D
2. A; f; h es paralelo a A; g; i, en que ambos tienen el mismo dominio y ambos tienen el mismo codominio.
3. A no es paralelo a ninguno de los otros nueve caminos.
Los morfismos en el diagrama dado son los siguientes:
A, A; f, A; g, A; j, B, B; h, C, C; i, D
Obsérvese que A; f; h = j = A; g; i.
Hay cuatro morfismos en D, que se muestran a continuación, a saber, z, s; s, y s; s; s; s:
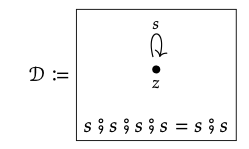
A continuación se muestran las ecuaciones que convierten las gráficas en preordenes
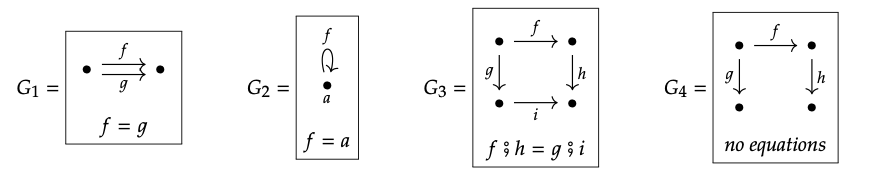
El reflejo de preorden de una categoría C tiene los mismos objetos y ya sea un morfismo o ninguno entre dos objetos, dependiendo de si existe o no un morfismo entre ellos en C. Entonces el reflejo de preorden de\(\mathbb{N}\) tiene un objeto y un morfismo de él a sí mismo, que debe ser la identidad. En otras palabras, el reflejo de preorden de\(\mathbb{N}\) es 1.
Una función f:\(\underline{2}\) →\(\underline{3}\) puede describirse como un par ordenado (f (1), f (2)). Las nueve funciones de este tipo están dadas por los siguientes pares ordenados, que organizamos en una cuadrícula bidimensional con 3 entradas en cada dimensión, solo para “funzies”:\(^{1}\)
(1, 1) (2, 1) (3, 1)
(1, 2) (2, 2) (3, 2)
(1, 3) (2, 3) (3, 3)
1. La inversa a f (a) = 2, f (b) = 1, f (c) = 3 viene dada por
f\(^{−1}\) (1) = b, f\(^{−1}\) 2) = a, f\(^{−1}\) (3) = c.
2. Hay 6 isomorfismos distintos. En general, si A y B son conjuntos, cada uno con n elementos, entonces el número de isomorfismos entre ellos es n factorial, a menudo denotado n!. Entonces por ejemplo hay 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1 = 120 isomorfismos entre {1, 2, 3, 4, 5} y {a, b, c, d, e}.
Tenemos que demostrar que para cualquier objeto c\(\in\) C, la identidad id c tiene una inversa, es decir, un morfismo f: c → c tal que f; id\(_{c}\) = id\(_{c}\) e id\(_{c}\); f = id\(_{c}\). Toma f = id\(_{c}\); esto funciona.
1. El monoide en el Ejemplo 3.13 no es un grupo, porque el morfismo s no tiene inversa.
Efectivamente cada morfismo es de la forma s\(^{n}\) para algunos n\(\in\)\(\mathbb{N}\) y componiéndolo con s da s\(^{n+1}\), que nunca es s.\(^{0}\) p
2. C del Ejemplo 3.18 es un grupo: la identidad es siempre un isomorfismo, y el otro morfismo s tiene s inverso.
¡Es posible que hayas encontrado a una persona cuyas afirmaciones matemáticas puedes confiar! Siempre que compongas dos morfismos en Libre (G), sus longitudes se suman, y las identidades son exactamente aquellos morfismos cuya longitud es 0. Para que p sea un isomorfismo, debe haber alguna q tal que p; q = id y q; p = id, en cuyo caso la longitud de p (o q) debe ser 0.
Los otros tres funtores 2 → 3 se muestran aquí:
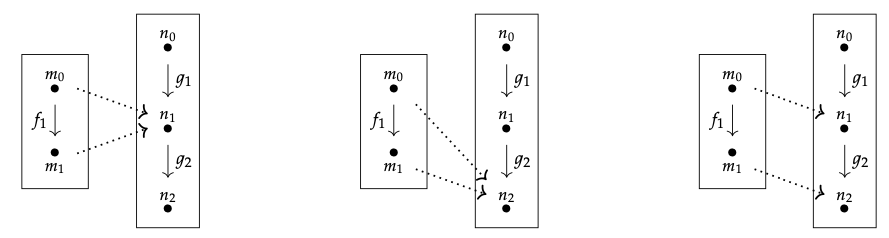
Hay nueve morfismos en F; como de costumbre denotamos identidades por el objeto en el que están. Estos morfismos son enviados a los siguientes morfismos en C:
A '\(\longmapsto\)A, f'\(\longmapsto\) f, g'\(\longmapsto\) g, f'; h'\(\longmapsto\) f; h, g'; i'\(\longmapsto\) f; h,
B ′\(\longmapsto\) B, h ′\(\longmapsto\) h, C ′\(\longmapsto\) C, i ′\(\longmapsto\) i, \(\longmapsto\)D ′ D.
Si uno de estos parece diferente al resto, probablemente sea g'; i'\(\longmapsto\) f; h.
Pero tenga en cuenta que de hecho también g'; i '\(\longmapsto\)g; i porque g; i = f; h, entonces no es un valor atípico después de todo.
Tenemos que dar dos funtores F, G de\(\stackrel{a}{\bullet} \stackrel{f}{\longrightarrow} \stackrel{b}{\bullet}\) a\(\stackrel{a'}{\bullet} \underset{f_{2}}{\stackrel{f_{1}}{\longrightarrow}} \stackrel{b'}{\bullet}\) cuyas partes on-objects son iguales y cuyas partes on-morfismos son diferentes. Solo hay dos formas de hacerlo, y elegimos una de ellas:
F (a) := a ′, G (a) := a ′, F (b) := b ′, G (b) := b ′, F (f) := f\(_{1}\), y G (f) := f\(_{2}\).
La otra manera invierte f\(_{1}\) y f\(_{2}\).
1. Que C sea una categoría.
Luego definir id\(_{C}\): C → C por id\(_{C}\) (x) = x para cada objeto y el morfismo en C es un functor porque conserva identidades id\(_{C}\) (id\(_{c}\)) = id\(_{c}\) = id\(_{id_{C}}\) (c) para cada objeto c\(\in\) Ob (C), y conserva la composición id\(_{C}\) (f; g) = f; g = id\(_{C}\) (f); id\(_{C}\) (\(_{g}\)) para cada par de morfismos componibles f, g en C.
2. Dados los funtores F: C → D y G: D → E, necesitamos demostrar que F; G es un functor, es decir, que conserva identidades y composiciones. Si c\(\in\) C es un objeto entonces (F; G) (id\(_{c}\)) = G (F (id\(_{c}\))) = G (id\(_{F(c)}\)) = id\(_{G(F(c)}\)) porque F y G conservan identidades. Si f, g son morfismos componibles en C entonces
(F; G) (f; g) = G (F (f); F (g)) = G (F (f)); G (F (g))
porque F y G conservan la composición
3. Se han propuesto objetos, morfismos, identidades y una fórmula de composición para una categoría Cat: son categorías, funtores, y las identidades y composiciones dadas anteriormente. Tenemos que comprobar que las dos propiedades, la unidad y la asociatividad, se mantienen. Entonces supongamos que F: C → D es un functor y lo precomponemos como arriba con id\(_{C}\); es fácil ver que el resultado volverá a ser F, y de manera similar si poscomponemos F con id\(_{D}\). Esto da unidad, y la asociatividad es igual de fácil, aunque más verdosa. Dado F como arriba y G: D →\(\mathcal{E}\) y H:\(\mathcal{E}\) → F, necesitamos mostrar que (F; G); H = F; (G; H). Es una simple aplicación de la definición: para cualquier x\(\in\) C, ya sea un objeto o morfismo, tenemos
((F; G); H) (c) = H ((F; G)) (c)) = H (G (F (c))) = (G; H) (F (c)) = (F (c)) = (F ; (G; H)) c).
Deje que S\(\in\) Set sea un conjunto. Definir F\(\_{S}\): 1 → Establecer por F\(\_{S}\) (1) = S y F\(\_{S}\) (id\(\_{1}\)) = id\(\_{S}\). Con esta definición, F\(\_{S}\) conserva identidades y composiciones (las únicas composiciones en 1 es el compuesto de la identidad consigo misma), por lo que F\(\_{S}\) es un funtor con F\(\_{S}\) (1) = S como se desee.
Se nos pregunta qué tipo de datos “tiene sentido” para los esquemas a continuación?
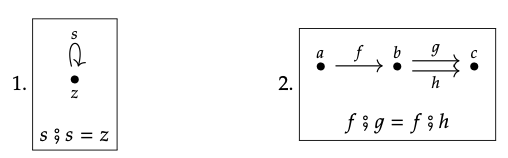
Esta es una pregunta subjetiva, por lo que proponemos una respuesta para su consideración.
1. Los datos de este esquema, es decir, un functor de valor establecido, asignan un conjunto D (z) y una función D (s): D (z) → D (z), de tal manera que aplicar esa función dos veces es la identidad. Este tipo de función se llama involución
del conjunto D z:
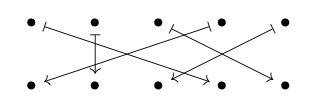
Es un do-si-do, un “movimiento de pareja”, donde todos eligen una pareja (posiblemente ellos mismos) y
intercambios con ellos. Un ejemplo se podría tomar D como el conjunto de píxeles en una fotografía, y tomar s para ser la función que envía cada píxel a su imagen especular a través de la línea central vertical de la fotografía.
2. Podríamos hacer D (c) estasetofpeopleata “SecretSanta” fiesta de Navidad, donde cada uno da un regalo a alguien, posiblemente a sí mismos. Tomar D (b) para ser el conjunto de regalos, g la función de dador (cada regalo es dado por una persona), y h la función receptora (cada regalo es recibido por una persona), D (a) es el conjunto de personas que se dan un regalo a sí mismas, y d f): D (a) → D (b) es la inclusión.
1. ¡El experto empaca tanta información en tan poco espacio! Supongamos dados tres objetos F, G, H\(\in\) D\(^{C}\); estos son los funtores F, G, H: C → D. Los morfismos α: F → G y β: G → H son transforaciones naturales. La mayoría de los principiantes parecen pensar en una transformación natural en cuanto a sus cuadrados de naturalidad, pero lo principal a tener en cuenta son sus componentes; los cuadrados de naturalidad constituyen un cheque que viene después.
Entonces para cada c\(\in\) C, α tiene un componente α\(_{c}\): F (c) → G (c) y β tiene un componente β\(_{c}\): G (c) → H (c) en D. El experto nos ha dicho que define (α; β)\(_{c}\): = (α\(_{c}\); β\(_{c}\)), y de hecho eso es un morfismo F (c) → H (c).
Ahora hacemos el chequeo. Para cualquier f: c → c ′ en C, los cuadrados internos del siguiente diagrama conmutan porque α y β son naturales; de ahí que el rectángulo exterior también lo haga:
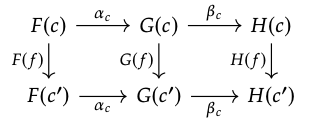
2. Proponemos que la identidad de transformación natural id\(_{F}\) en un functor F: C → D tiene como componente c el morfismo (id\(_{F}\))\(_{c}\): = id\(_{F}\) (\(_{c}\)) en D, para cualquier c. La plaza de la naturalidad
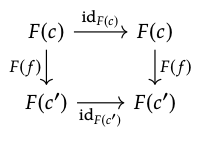
obviamente viaja por cualquier f: c → c ′. Y es unital: postcomponer id F con cualquier β: F → G (y de manera similar para precomponer con cualquier α: E → F) da como resultado una transformación natural id\(_{F}\); β con componentes (id\(_{F}\))\(_{c}\) ; β\(_{c}\) = (id\(_{F}\) (\(_{c}\)); β\(_{c}\)) = β\(_{c}\), y esto es solo β como se desee.
Tenemos una categoría C y una preorden P, considerada como categoría.
1. Supongamos que F, G: C → P son funtores y α, β: F → G son transformaciones naturales; necesitamos mostrar que α = β.
Basta con comprobar que α c\(_{c}\) = β\(_{c}\) para cada objeto c\(\in\) Ob (C). Pero α\(_{c}\) y β\(_{c}\) son morfismos F (c) → G (c) en P, que es un preorden, y la definición de un preorden considerado como categoría es que tiene como máximo un morfismo entre dos objetos cualesquiera. Así α\(_{c}\) = β\(_{c}\), según se desee.
2. Esto es falso. Dejar P: = 1, dejar C: =\(\stackrel{a}{\bullet} \frac{f_{1}}{f_{2}} \text { b }\), dejar F (1) := a, dejar G (1) := b, dejar α\(_{1}\) := f\(_{1}\), y dejar β\(_{1}\) := g\(_{2}\).
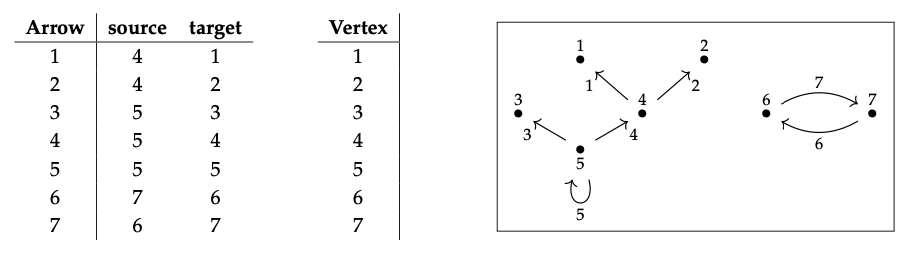
Tenemos que anotar lo siguiente
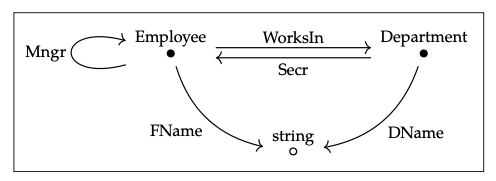
como una instancia Gr, como en la Ec. (3.61). La respuesta es la siguiente:

Sea G, H las siguientes gráficas:

y vamos a creer a los autores que existe una gráfica única homomorfismo α: G → H para la cual α\(_{Arrow}\) (a) = d.
- Tenemos α\(_{Arrow}\) (b) = e y α\(_{Vertex}\) (1) = 4, α\(_{Vertex}\) (2) = 5, y α\(_{Vertex}\) (3) = 5.
- Copiamos aproximadamente las tablas y luego dibujamos las líneas (mostradas en negro; ignoramos las líneas discontinuas por ahora):
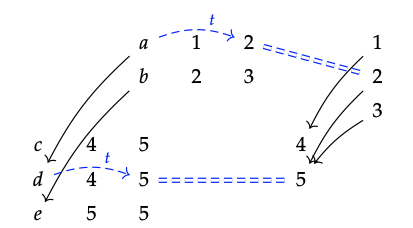
3. ¡Funciona! Un ejemplo de la naturalidad se muestra con la ayuda de líneas azules discontinuas arriba. ¿Ves cómo ambos caminos empiezan por un final a las 5?
Solo necesitamos escribir el compuesto de los siguientes funtores
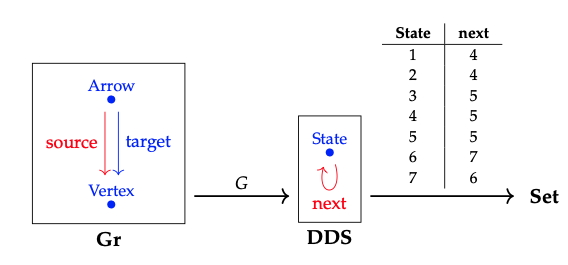
en forma de base de datos, y luego dibujar la gráfica. Los resultados se dan a continuación.
Nos interesa cómo\(^{B}\) deben actuar los funtores − × B y (−) sobre los morfismos para un determinado conjunto B.
No especificamos esto en el texto —solo especificamos − × B y (−)\(^{B}\) en objetos así que en algún sentido este ejercicio es abierto: puedes inventar lo que quieras, bajo la condición de que sea funciontorial. Sin embargo, los autores no pueden pensar en ninguna de esas respuestas excepto la que damos a continuación.
1. Dada una función arbitraria f: X → Y, necesitamos una función X × B → Y × B. Sugerimos la función que podría ser denotada f × B; envía (x, b) a (f (x), b). Esta asignación es funcionaria: aplicada a id\(_{X}\) devuelve id\(_{X x B}\) y conserva la composición.
2. Dada una función f: X → Y, necesitamos una función X\(^{B}\) → Y\(^{B}\). La función canónica se denotaría f\(^{B}\); envía una función g: B → X al compuesto (g; f): B → X → Y. Esto es funciontorial: aplicado a id\(_{X}\) envía g a g, es decir, f\(^{B}\) (id\(_{X}\)) = id\(_{X}\)\(^{B}\), y aplicado al compuesto (f\(_{1}\); f\(_{2}\)): X → Y → Z, tenemos
(f\(_{1}\); f\(_{2}\))\(^{B}\) (g) = g; (f\(_{1}\); f\(_{2}\)) = (g; f\(_{1}\)); f\(_{2}\) = (f\(_{1}\)\(^{B}\); f\(_{2}\)\(^{B}\)) g
para cualquier g\(\in\)\(^{B}\) X.
3. Si p:\(\mathbb{N}\) →\(\mathbb{N}\)\(^{\mathbb{N}}\) es el resultado de currying +:\(\mathbb{N}\) ×\(\mathbb{N}\) →\(\mathbb{N}\), entonces p (3) es un elemento de\(\mathbb{N}\)\(^{\mathbb{N}}\), es decir tenemos p (3):\(\mathbb{N}\) →\(\mathbb{N}\) ¿qué función es? Es la función la que suma tres. Eso es p (3) (n) := n + 3.
¡El funtor! : C → 1 de la Ec. (3.75) envía cada objeto \(\in\)c C al objeto único\(\in\) 1 1 y envía cada morfismo f: c → d en C al morfismo único id\(_{1}\): 1 → 1 en 1.
Queremos dibujar la gráfica correspondiente a la instancia I: G → Conjunto que se muestra a continuación:

Aquí está, con nombres y correos electrónicos acortados (por ejemplo, B=Bob, 3=Em_3):
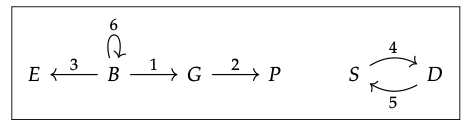
Un objeto z es terminal en alguna categoría C si, por cada c\(\in\) C existe un morfismo único c → z. Cuando C es la categoría subyacente a un preorden, hay como máximo un morfismo entre dos objetos cualesquiera, por lo que la condición simplifica: un objeto z es terminal iff, por cada \(\in\)c C existe un morfismo c → z. Los morfismos en un preorden se escriben con ≤ signos, por lo que z es terminal iff, por cada c\(\in\) P tenemos c ≤ z, y esta es la definición de elemento superior.
El objeto terminal en Cat es 1 porque por el Ejercicio 3.76 hay un morfismo único (functor) C → 1 para cualquier objeto (categoría) C\(\in\) Cat.
Considera la gráfica 2 V: = • • con dos vértices y sin flechas, y deja C = Libre (2 V); tiene dos objetos y dos morfismos (las identidades). Esta categoría no tiene un objeto terminal porque no tiene morfismos de un objeto a otro.
Un producto de x e y en P es un objeto z\(\in\) P equipado con mapas z → x y z → y de manera que para cualquier otro objeto z′ y mapas z ′ → x y z ′ → y, hay un morfismo único z ′ → z haciendo que los triángulos evidentes viajen. Pero en un preorden, los mapas se denotan ≤, son únicos si existen, y todos los diagramas se desplazan. Así lo anterior se convierte en: un producto de x e y en P es un objeto z con z ≤ x y z ≤ y tal que para cualquier otro z ′, si z ′ ≤ x y z ′ ≤ y luego z ′ ≤ z. Esta es exactamente la definición de meet, z = x\(\land\) y.
1. El morfismo de identidad sobre el objeto (c, d) en la categoría de producto C × D es (id\(_{c}\), id (_ {d}\)).
2. Supongamos dados tres morfismos componibles en C × D
\((c\(_{1}\), d\(_{1}\))\ stackrel {(f\(_{1}\), g\(_{1}\)})} {\ rightarrow} (c\(_{2}\), d\(_{2}\)\ stackrel {(f\(_{2}\), g\(_{2}\)})} {\ rightarrow} (c\(_{3}\), d\(_{3}\)\ stackrel {(f\(_{3}\), g\(_{3}\)})} {\ rightarrow} (c\(_{4}\), d \(_{4}\)\)
Queremos verificar que ((f\(_{1}\), g\(_{1}\)); (f, g); (f\(_{2}\), g\(_{2}\)) = (f\(_{3}\), g\(_{3}\)); (f\(_{1}\), g\(_{1}\)); ((f\(_{2}\), g \(_{2}\)); (f\(_{3}\), g\(_{3}\)). Pero la composición en una categoría de producto se da en cuanto a componentes. Eso significa que el lado izquierdo es ((f\(_{1}\); f\(_{2}\)); f\(_{3}\), (g\(_{1}\); g\(_{2}\)); g\(_{3}\)), mientras que el lado derecho es (f\(_{1}\); (f; (f \(_{2}\); f\(_{3}\)), g\(_{1}\); (g\(_{2}\); g\(_{3}\))), y estos son iguales porque tanto C como D individualmente tienen composición asociativa.
3. La categoría de producto 1 × 2 tiene dos objetos (1, 1) y (1, 2) y un morfismo no identitario (1,1) → (1,2). No es difícil ver que se ve igual que 2. De hecho, para cualquier C hay un isomorfismo de categorías 1 × C\(\cong\) C.
4. Que P y Q sean prepedidos, que X = P × Q sean su preorden de producto como se define en el Ejemplo 1.56, y dejar que P, Q y X sean las categorías correspondientes. Entonces X = P × Q.
Un producto de X e Y es un objeto Z equipado con morfismos\(X \stackrel{px}{\leftarrow} Z \stackrel{py}{\rightarrow} Y\) tales que para cualquier otro objeto Z' equipado con morfismos\(X \stackrel{p'x}{\leftarrow} Z \stackrel{p'y}{\rightarrow} Y\), hay un morfismo único f: Z → Z haciendo que los triángulos viajen, f; p\(_{X}\) = p ′\(_{X}\) y f; p\(_{Y}\) = p ′\(_{Y}\). Pero “un objeto equipado con morfismos a X e Y” es exactamente la definición de un objeto en Cono (X, Y), y un morfismo f haciendo que los triángulos viajen es exactamente la definición de un morfismo en Cono ( X, Y). Entonces la definición anterior se convierte en: un producto de X e Y es un objeto Z\(\in\) Cono (X, Y) tal que para cualquier otro objeto Z ′ hay un morfismo único Z ′ → Z en Cono (X, Y). Esta es exactamente la definición de Z siendo terminal en Cono (X, Y).
Supongamos que J es la gráfica\(\begin{array}{l} v1 \\ \bullet \end{array}\)\(\begin{array}{l} v2 \\ \bullet \end{array}\) y D: J → Conjunto viene dado por dos conjuntos, D (v\(_{1}\)) = A y D (v\(_{2}\)) = B para los conjuntos A, B. El producto de estos dos juegos es A × B. Comprobemos que la fórmula límite en Teorema 3.95 da la misma respuesta. Dice
\ (\ begin {aligned}
&\ lim _ {g} D: =\ left\ {\ left (d_ {1},\ ldots, d_ {n}\ right)\ mid d_ {i}\ in D\ left (v_ {i}\ right)\ text {para todos} 1\ leq i\ leq n\ derecho. \ texto {y}\\
&\ texto {para todos} a: v_ {i}\ fila derecha v_ {j}\ en A,\ texto {tenemos}\ izquierda.d (a)\ izquierda (d_ {i}\ derecha) =d_ {j}\ derecha\ derecha\}
\ fin {alineada}\)
Pero en nuestro caso n = 2, no hay flechas en la gráfica, y D (v\(_{1}\)) = A y D (v\(_{2}\)) = B. Entonces la fórmula se reduce a
lim\(_{J}\) D := (d\(_{1}\), d\(_{2}\)) | d\(_{1}\)\(\in\) A y d\(_{2}\)\(\in\) B.
que es exactamente la definición de A × B.
Dado un functor F: C → D, definimos su opuesto F\(^{op}\): C\(^{op}\) → D de la\(^{op}\) siguiente manera.
Para cada objeto c\(\in\) Ob (C\(^{op}\)) = Ob (C), ponga F\(^{op}\) (c) := F (c). Por cada morfismo f: c\(_{1}\) → c\(_{2}\) en C\(^{op}\), tenemos un morfismo correspondiente f ′: c\(_{2}\) → c\(_{1}\) en C y así un morfismo F (f ′): F (c\(_{2}\)) → F (c\(_{1}\)) en D, y así un morfismo F (f): F\(^{op}\) (c\(_{1}\)) → F\(^{op}\) (c\(_{2}\)).
De ahí que podamos definir F\(^{op}\) (f) := F (f') '. Tenga en cuenta que los primos (−') son bastante carentes de sentido, solo los ponemos ahí para diferenciar entre cosas que están muy estrechamente relacionadas. Es fácil comprobar que nuestra definición de F op es funcionaria: envía identidades a identidades y composites a composites.


