8.4: Soluciones para el Capítulo 4
- Page ID
- 112244
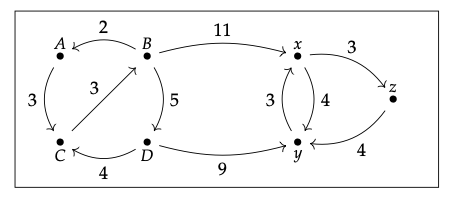
1. Aquí se muestra el diagrama de Hasse para Xop × Y (ignore los colores):
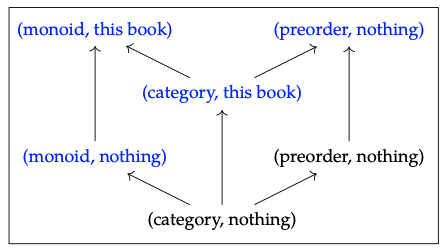
2. Hay un profunctor\(\land\): X → Y, es decir, un functor X\(^{op}\) × Y → B, tal que, en la imagen de arriba, el azul se envía a true y el negro se envía a false, i.e.
\(\land\)(monoide, nada) =\(\land\) (monoide, este libro)
=\(\land\) (preorden, este libro) =\(\land\) (categoría, este libro) = verdadero
\(\land\)(preorden, nada) =\(\land\) (categoría, nada) = falso.
El preorden X\(^{op}\) × Y describe tareas en dificultad decreciente. Por ejemplo, (esperamos) es más fácil para mi tía explicar un monoide dado este libro que para ella explicar un monoide sin este libro. El profunctor\(\land\) describe posibles estados de conocimiento para mi tía: puede describir monoides sin ayuda, categorías con ayuda del libro, etc. Es un conjunto superior porque suponemos que si puede hacer una tarea, también puede hacer cualquier tarea más fácil.
¡Ya hemos hecho esto antes! Esperamos que hayas recordado cómo hacerlo. Si no, ver Ejercicio 2.84.
Recordemos de la Definición 2.41 que un V-functor Φ: X\(^{op}\) × Y → V es una función Φ: Ob (X\(^{op}\) × Y) → Ob (V) tal que para todos (x, y) y (x ′, y ′) en X\(^{op}\) ×Y tenemos
(X\(^{op}\) ×Y) ((x, y), (x', y')) ≤ V (Φ (x, y), Φ (x', y')).
Usando las definiciones de categoría V del producto (Definición 2.74) y categoría V opuesta (Ejercicio 2.73) en el lado izquierdo, y usando Observación 2.89, que describe cómo estamos viendo la cuantale V enriquecida sobre sí misma, en el lado derecho, esto desempaqueta para
X (x ′, x) Y (y, y ′) ≤ Φ (x, y) -o Φ (x ′, y ′)
Usando la simetría de y la definición de hom-elemento, Ec. (2.80), vemos que Φ es un profunctor si y solo si
X (x ′, x) Φ (x, y) Y (y, y ′) ≤ Φ (x ′, y ′).
Sí, ya que un Bool -functor es exactamente lo mismo que un mapa monótono, ¡la definición de Bool -profunctor y la de relación de factibilidad se alinean perfectamente!
La matriz de factibilidad para Φ es

La matriz de costo para Φ es
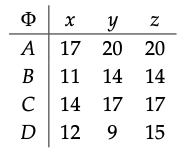
\ (\ begin {alineado}
\ Phi=M_ {X} ^ {3} * M_ {\ Phi} * M_ {Y} ^ {2} &=\ left (\ begin {array} {cccc}
0 & 6 & 3 & 11\\
2 & 0 & 5 & 5 &
5 & 3 & 0 & 8\\
11 & 9 & 6 & 0
\ end {array}\ derecha)\ left (\ begin {array} {ccc}
\ infty &\ infty &\ infty\\ infty\\
11 &\ infty &\ infty
\\ infty &\ infty &\ infty
\\ infty & 9 &\ infty
\ end {array}\ right)\ left (\ begin {array} {ccc}
0 & 4 & 3\\
3 & 0 & 6\\
7 & 4 & 0
\ end {array}\ right)\\
&=\ left (\ begin {array} {ccc}
17 & 20 &\ infty\\
11 & 14 &\ infty\\
14 & 17 &\ infty\\
20 & 9 &\ infty
\ end {array}\ derecha)\ left (\ begin {array} {lll}
0 & 4 & 3\\
3 & 0 & 6\\
7 & 4 & 0
\ end {array}\ derecha)\\
&=\ left (\ begin {array} {ccc}
17 & 20 & 20\\
11 & 14 & 14\\
14 & 17 & 17\\
12 & 9 & 15
\ end {array}\ derecha)
\ end {alineado}\)
Sí, esto es válido: solo significa que el profunctor Φ: (T × E) → $ no se relaciona (bondadoso, gracioso) con ningún elemento de $. De manera más formal, significa que Φ ((bondadoso, gracioso), p) = falso para todos p\(\in\) $ = {$100K, $500K, $1M}. Podemos interpretar esto en el sentido de que no es factible producir una película bondadosa y divertida para ninguna de las opciones de costo que se presentan, así que al menos no por menos de un millón de dólares.
Hay una serie de métodos que se pueden utilizar para obtener la respuesta correcta. Una forma que funciona bien para este ejemplo es buscar los caminos más cortos en el diagrama: sucede que todos los caminos más cortos pasan por los puentes de D a y e y a r, así que en este caso (Φ; ψ) (−, −) = X (−, D) + 9 + Z (r , −). Esto da:
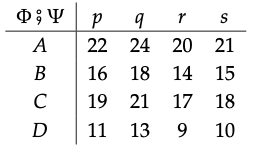
Una forma más metódica es utilizar la multiplicación matricial. Aquí hay una forma en la que podrías hacer la multiplicación, usando algunos trucos.
\ (\ begin {alineado}
\ Phi_ {9} ^ {\ circ}\ Psi &=\ izquierda (M_ {X} ^ {3} * M_ {\ Phi} * M_ {Y} ^ {2}\ derecha) *\ izquierda (M_ {Y} ^ {2} * M_ {\ Psi} * M_ {Z} ^ {3}\ derecha)\\
&=M_ {X} ^ {3} * M_ {\ Phi} * M_ {Y} ^ {4} * M_ {\ Psi} * M_ {Z} ^ {3}\\
&=\ izquierda (M_ {X} ^ {3} * M_ {\ Phi} * M_ {Y} ^ {2}\ derecha) * M_ {\ Psi} * M_ {Z} ^ {3}\\
&=\ Phi * M_ {\ Psi} * M_ {Z} ^ {3}\\
&=\ left (\ begin {array} {lll}
17 & 20 & 20\\
11 & 14 &
14 & 17 & 17\\
12 & 9 & 15
\ end {array}\ derecha)\ left (\ begin { array} {llll}
\ infty &\ infty &\ infty &\ infty\
\ infty &\ infty &\ infty &\ infty &\
infty &\ infty &\ infty & 4
\ end {array}\ derecha)\ left (\ begin {array} {llll}
0 & 2 & 4 & 5\\
4 & amp; 0 & 2 & 3\\
2 & 4 & 0 & 1\\
1 & 3 & 5 & 0
\ end {array}\ derecha)\\
&=\ left (\ begin {array} {lll}
17 & 20 & 20\\
11 & 14 & 14\\
14 & 17 & 17 & 17 \\
12 & 9 & 15
\ end {array}\ derecha)\ left (\ begin {array} {llll}
\ infty &\ infty &\ infty &\ infty &\ infty\\ infty\\
2 & 4 & 0 & 0 & 1\\
4 & 6 & 8 & 4
\ end {array}\ right)\
\ left (\ begin {array} {llll}
22 & 24 & 20 & 21\\
16 & 18 & 14 & 15\\
19 & 21 & 17 & 18\\
11 & 13 & 9 & 10
\ end {array}\ right)
\ end {alineado}\)
Elegimos la categoría Costo -X de la Eq. (2.56). El profunctor de la unidad U\(_{X}\) en X se describe en el diagrama de puente
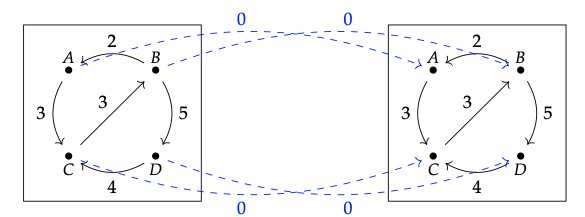
1. La primera igualdad es la unidad de V (Definición 2.2 (b)).
El segundo paso utiliza la monotonicidad de (Definición 2.2 (a)) aplicada a las desigualdades I ≤ P (p, p) (la ley de identidad para P en p, Definición 2.46 (a)) y Φ (p, q) ≤ Φ (p, q) (reflexividad de preorden V, Definición 1.30 (a)). El tercer paso utiliza la definición de unión: para todos x e y, ya que cualquier x ≤ x, tenemos x ≤ x\(\lor\) y. La igualdad final es solo la definición de composición profunctora, Definición 4.21.
2. Obsérvese que en Bool, I = verdadero.
Dado que la ley de identidad en p dice true ≤ P (p, p), y true es el elemento más grande del preorden Bool, tenemos así P (p, p) = true para todos p. Esto demuestra que la primera desigualdad en la ecuación (4.28) es una igualdad.
La segunda desigualdad está más involucrada. Obsérvese que por lo anterior, podemos suponer que el lado izquierdo de la desigualdad es igual a Φ (p, q). Nos dividimos en dos casos. Supongamos Φ (p, q) = verdadero. Entonces, nuevamente ya que la verdad es el elemento más grande de\(\mathbb{B}\), debemos tener igualdad.
A continuación, supongamos Φ (p, q) = falso. Obsérvese que dado que Φ es un mapa monótono P\(^{op}\) × Q → Bool, si p ≤ p en P, entonces Φ (p 1, q) ≤ Φ (p, q) en Bool.
Así, si P (p, p 1) = verdadero entonces Φ (p\(_{1}\), q) = Φ (p, q) = falso.
Esto implica que para todos p 1\(\in\) P, tenemos ya sea P (p, p\(_{1}\)) = falso o Φ (p\(_{1}\), q) = falso, y por lo tanto =\(\bigvee\)\(_{p_{1} \in\ P}\) P (p, p\(_{1}\))\(\land\) Φ (p \(_{1}\), q) =\(\bigvee\)\(_{p_{1} \in\ P}\) falso = falso.
Así, en cualquier caso, vemos que Φ (p, q) =\(\bigvee\)\(_{p_{1} \in\ P}\) P (p, p\(_{1}\))\(\land\) Φ (p\(_{1}\), q), según se requiera.
3. La primera ecuación es la unidad en categorías monoidales, v I = v para cualquier \(\in\)v V. La segunda es que I ≤ Q (q, q) por unidad de categorías enriquecidas, ver Definición 2.46, junto con monotonicidad del producto monoidal: v\(_{1}\) ≤ v\(_{2}\) implica v v\(_{1}\) ≤ v v\(_{2}\). El tercero se mostró en el Ejercicio 4.9.
Esto es muy similar al Ejercicio 2.104: explotamos la asociatividad de. Tenga en cuenta, sin embargo, que también requerimos que V sea cerrado monoidal simétrico, ya que esto implica la distributividad de sobre\(\lor\) (Proposición 2.87 2), y V sea esquelético, por lo que podemos convertir equivalencias en igualdades.
\ (\ begin {aligned}
((\ Phi\ text {;}\ Psi)\ text {;}\ Upsilon) (p, s) &=\ bigvee_ {r\ in\ mathcal {R}}\ left (\ bigvee_ {q\ in\ mathbb {Q}}\ Phi (p, q)\ otimes\ Psi (q, r)\ derecha)\ otimes\ Upsilon (r, s)\\
&=\ bigvee_ {r\ in\ mathcal {R}, q\ in\ mathbb {Q}}\ Phi (p, q)\ otimes\ Psi (q, r)\ otimes\ Upsilon (r, s)\\
&=\ bigvee_ {q\ in\ mathbb {Q}}\ Phi (p, q)\ otimes\ bigvee_ {r\ in\ mathcal {R}} (\ Psi (q, r)\ otimes\ Upsilon (r, s))\\
& =(\ Phi\ text {;} (\ Psi\ Psi\ text {;}\ Upsilon)) (p, s)
\ end {alineado}\)
Esto es muy sencillo. Deseamos verificar\(\widehat{id}\): P → P tiene la fórmula\(\widehat{id}\) (p, q) = P (p, q). Por Definición 4.34,\(\widehat{id}\) (p, q) := P (id (p), q) = P (p, q). Entonces son lo mismo.
El conjunto\(\check{+}\):\(\mathbb{R}\) →\(\mathbb{R}\) ×\(\mathbb{R}\) ×\(\mathbb{R}\) envía (a, b, c, d) a\(\mathbb{R}\) (a, b + c + d), que es verdadero si a ≤ b + c + d, y falso de otra manera.
1. Por Definición 4.34,\(\widehat{F}\) (p, q) = Q (F (p), q) y\(\check{G}\) (p, q) = Q (p, G (q)). Dado que V es esquelético, F y G son V anexos si y sólo si Q (F (p), q) = Q (p, G (q)). Así F y G son colindantes si y sólo si\(\widehat{F}\) =\(\check{G}\).
2. Tenga en cuenta que id: P → P es V-unido a sí mismo, ya que ambos lados de la Ec. (4.40) entonces son iguales a P (p, q). Así\(\widehat{id}\) =\(\check{id}\).
El diagrama de Hasse para el collage del profunctor dado es simplemente esto:
Como solo tenemos una definición aproximada, solo podemos verificar esto de manera aproximada: no nos molestaremos con la noción de buen comportamiento. No obstante, todavía podemos comparar la Definición 2.2 con la Definición 4.45.
Primero, recordemos de la Sección 3.2.3 que un preorden es una categoría P tal que por cada p, q\(\in\) P, el conjunto P (p, q) tiene como máximo un elemento.
En la superficie, todo parece prometedor: ambas definiciones tienen dos constituyentes y cuatro propiedades. En el constituyente (i), tanto la Definición 2.2 como la Definición 4.45 piden lo mismo: un elemento, u objeto, del preorden P. Hasta ahora tan bueno. Constituyente (ii), sin embargo, es donde se pone interesante: La definición 2.2 requiere meramente una función: P × P → P, mientras que la Definición 4.45 llama a un functor.
Recordemos del Ejemplo 3.42 que los funtores entre preordenes son exactamente mapas monótonos. Entonces necesitamos que la función en la Definición 2.2 sea un mapa monótona. Esta es exactamente la propiedad (a) de la Definición 2.2: dice que si (x\(_{1}\), x\(_{2}\)) ≤ (y\(_{1}\), y\(_{2}\)) en P P, entonces debemos\(_{1}\) tener x x\(_{2}\) ≤ \(_{1}\)y y \(_{2}\)en P. Así es también el caso de que en la Definición 2.2 que sea un funtor.
Las propiedades restantes se comparan fácilmente, tomando los isomorfismos naturales como igualdad o equivalencia en P. Efectivamente, la propiedad (b) de la Definición 2.2 corresponde a ambas propiedades (a) y (b) de la Definición 4.45, y luego las respectivas propiedades (c) y (d) corresponden de manera similar.
- \(_{gE}\)(5, 3) = falso,\(_{gF}\) (5, 3) = 2.
- \(_{gE}\)(3, 5) = verdadero,\(_{gF}\) (3, 5) = −2.
- h (5, verdadero) = 5.
- h (−5, verdadero) = −5.
- h (−5, falso) = 6.
- \(_{qG}\)(−2, 3) = 2,\(_{qF}\) (−2, 3) = −13.
- \(_{qG}\)(2, 3) = −1,\(_{qF}\) (2, 3) = 7.
Sí, la definición aproximada está de acuerdo aproximadamente: las categorías antiguas simples son Set -categorías! En detalle, necesitamos comparar la Definición 4.51 cuando V = (Set, {1}, ×) con la Definición 3.6. En ambos casos, vemos que (i) pide una colección de objetos y (ii) pide, para todos los pares de objetos x, y, un conjunto C (x, y) de morfismos. Además, recordemos que la unidad monoidal I es el conjunto de un elemento {1}.
Esto significa que un id de morfismo\(_{x}\): I → C (x, x) es un id de función\(_{x}\): {1} → C (x, x). Este es el mismo dato que simplemente un elemento id\(_{x}\) = id\(_{x}\) (1)\(\in\) C (x, x); llamamos a estos datos el morfismo de identidad en x. Finalmente, un morfismo;: C (x, y) C (y, z) → C (x, z) es una función;: C (x, y) × C (y, z) → C (x, z); este es exactamente el compuesto requerido en la Definición 3.6 (iv).
Por lo que en ambos casos los datos están de acuerdo. En la Definición 3.6 también requerimos de estos datos para saciar dos condiciones, la unidad y la asociatividad. Esto es lo que se entiende por la última frase de la Definición 4.51.
Un elemento de identidad en una categoría Costo -X es un morfismo I → X (x, x) en Costo = ([0, ∞], ≥, 0, +), y de ahí la condición de que 0 ≥ X (x, x). Esto implica que X (x, x) = 0. En cuanto a las distancias, interpretamos esto en el sentido de que la distancia desde cualquier punto a sí mismo es igual a 0. Creemos que esta es una condición bastante sensata para que una noción de distancia obedezca.
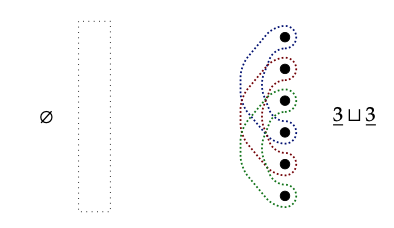
1. Aquí hay una imagen de la corelación unitaria Ø →\(\underline{3}\)\(\underline{3}\), donde hemos dibujado el conjunto vacío con un rectángulo punteado vacío a la izquierda:
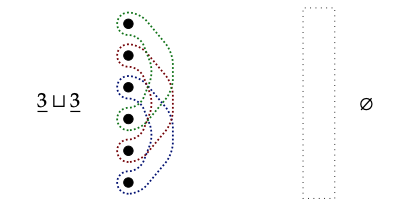
2. Aquí hay una imagen de la corelación\(\underline{3}\) counit\(\underline{3}\) → Ø:
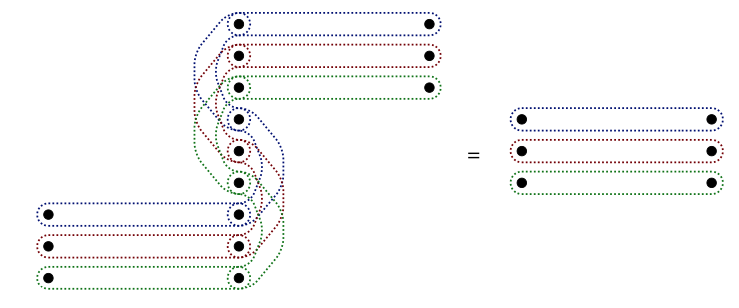
3. Aquí hay una imagen de la ecuación de serpiente a la izquierda de la ecuación (4.59).
Dados dos preordenes de recursos X e Y, el preorden X × Y representa el conjunto de todos los pares de recursos, \(\in\)x X e y \(\in\)Y, con (x, y) ≤ (x ′, y ′) iff x ≤ x ′ e y ≤ y ′. Es decir, si x está disponible dado x ′ e y está disponible dado y ′, entonces (x, y) está disponible dado (x ′, y ′).
Dados dos profactores Φ: X\(_{1}\) → X\(_{2}\) y ψ: Y\(_{1}\) → Y\(_{2}\), el profunctor Φ × ψ representa su conjunción, es decir, Y. En otras palabras, si y se\(_{1}\) puede obtener dado x\(_{1}\) Y y se\(_{2}\) puede obtener dado x\(_{2}\), entonces (y\(_{1}\), y\(_{2}\)) se puede obtener dado (x\(_{1}\), x\(_{2}\)).
El profunctor X × 1 → X definido por el funtor α: (X × 1)\(^{op}\) × X → V que mapea α ((x, 1), y) := X (x, y) es un isomorfismo. Tiene α inversa\(^{-1}\): X → X × 1 definida por α\(^{-1}\) (x, (y, 1)) := X (x, y). Para ver que α\(^{-1}\); α = U\(_{x}\), anotar primero que la ley unitaria para X en z y la definición de join implican
X (x, z) = X (x, z) I ≤ X (x, z) X (z, z) ≤\(\bigvee_{y \in X}\) X (x, y) X (y, z),
mientras que la composición dice X (x, y) X (y, z) ≤ X (x, z) y por lo tanto
\(\bigvee_{y \in X}\)X (x, y) X (y, z) ≤\(\bigvee_{y \in X}\) X (x, z) X (y, z)
Así, desempaquetando la definición de composición de profunctor, tenemos
(α\(^{-1}\); α) (x, z) =\(\bigvee_{(y,1) \in Xx1}\) α (x, (y, 1)) α\(^{-1}\) ((y, 1), z) =\(\bigvee_{y \in X}\) X (x, y) X (y, z) = X (x, z).
Del mismo modo podemos mostrar α; α\(^{−1}\) = U\(_{X×1}\), y de ahí que α es un isomorfismo X × 1 → X. Además, podemos mostrar de manera similar que β ((1, x), y) := X (x, y) define un isomorfismo β: 1 × X → X.
Comprobamos la primera ecuación de serpiente, la del lado izquierdo de la ecuación (4.59). La prueba de la del lado derecho es análoga. Debemos demostrar que el Φ compuesto de profunctores
\(X \stackrel{a^{-1}}{\rightarrow} X x 1 \stackrel{U_{x} x n_{x}}{\longrightarrow} X x X^{op} x X \stackrel{\mathcal{E}_{x} x U_{x}} {\longrightarrow} 1 x X \stackrel{a}{\rightarrow} X\)
es en sí misma la identidad (es decir, el profunctor unitario en X), donde α y α\(^{−1}\) son los isomorfismos definidos en la solución al Ejercicio 4.65 anterior.
Usando libremente la distributividad de sobre\(\land\), el valor Φ (x, y) de este compuesto en (x, y)\(\in\) X\(^{op}\) × X viene dado por
\ (\ begin {alineado}
&\ bigvee_ {x}\ alpha^ {-1} (x, (a, 1))\ oveces (\ mathrm {U} x\ veces\ eta x) ((a, 1), (b, c, d))\\
& a, b, c, d, e\ en X &\ oveces (\ épsilon x\ veces\ mathrm {U} x) ((b, c, d), (1, e))\ oveces\ alfa ((1, e), y)\\
=&\ bigvee_ {\ alpha} ^ {-1} (x, (a, 1))\ otimes\ mathrm {U} x (a, b)\ otimes\ eta x (1, c, d)\\
& a, b, c, d, e\ in\ mathcal {X}\ quad\ otimes\ epsilon x (b, c, 1)\ otimes\ mathrm {U} x (d, e)\ otimes\ alpha ((1, e), y)\\
=&\ bigvee_ {a, b, c, d, e\ en X}\\
=& x (x, y)
\ end {alineado}\)
donde en el paso final utilizamos repetidamente el argumento el Lema 4.27 que demuestra que componer con la unidad profunctor U\(_{X}\) (a, b) = X (a, b) es la identidad. Esto muestra que Φ (x, y) es el profunctor de identidad, y por lo tanto muestra la primera ecuación de serpiente que sostiene. Nuevamente, comprobar la otra ecuación de serpiente es análogo.


