4.4: Multiplicación de Fracciones

Última actualización
Guardar como PDF

Page ID: 116748

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

entender el concepto de multiplicación de fracciones
poder multiplicar una fracción por otra
ser capaz de multiplicar números mixtos
ser capaz de encontrar poderes y raíces de diversas fracciones

Fracciones de Fracciones

Sabemos que una fracción representa una parte de una cantidad entera. Por ejemplo, dos quintas partes de una unidad pueden ser representadas por

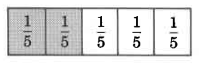
$Un rectángulo dividido equitativamente en cinco partes. Cada parte está etiquetada como una quinta parte. Dos de las partes están sombreadas.$

$\dfrac{2}{5}$del conjunto está sombreado.

Una pregunta natural es, ¿qué es una parte fraccionaria de una cantidad fraccionaria, o, qué es una fracción de una fracción? Por ejemplo, ¿$\dfrac{2}{3}$de qué$\dfrac{1}{2}$?

Podemos sugerir una respuesta a esta pregunta usando una imagen para examinar$\dfrac{2}{3}$$\dfrac{1}{2}$.

Primero, representemos$\dfrac{1}{2}$.

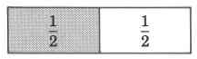
$Un rectángulo dividido equitativamente en dos partes. Ambas partes están etiquetadas como la mitad. Una de las partes está sombreada.$

$\dfrac{1}{2}$del conjunto está sombreado.

Luego divide cada una de las$\dfrac{1}{2}$ partes en 3 partes iguales.

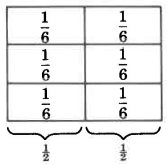
$Un rectángulo dividido en seis partes iguales en forma de cuadrícula, con tres filas y dos columnas. Cada parte está etiquetada como una sexta parte. Debajo de los rectángulos hay corchetes que muestran que cada columna de sextos es igual a la mitad.$

Cada parte es$\dfrac{1}{6}$ del todo.

Ahora tomaremos$\dfrac{2}{3}$ de la$\dfrac{1}{2}$ unidad.

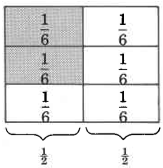
$\dfrac{2}{3}$de$\dfrac{1}{2}$ es$\dfrac{2}{6}$, lo que reduce a$\dfrac{1}{3}$.

Multiplicación de Fracciones

Ahora nos preguntamos, ¿qué operación aritmética$(+, - , \times , \div)$ producirá$\dfrac{2}{6}$ a partir$\dfrac{2}{3}$ de$\dfrac{1}{2}$?

Observe que, si en las fracciones$\dfrac{2}{3}$ y$\dfrac{1}{2}$, multiplicamos los numeradores juntos y los denominadores juntos, obtenemos precisamente$\dfrac{2}{6}$.

$\dfrac{2 \cdot 1}{3 \cdot 2} = \dfrac{2}{6}$

Esto se reduce a$\dfrac{1}{3}$ como antes.

Usando esta observación, podemos sugerir lo siguiente:

La palabra “de” se traduce como la operación aritmética “tiempos”.
Para multiplicar dos o más fracciones, multiplicar los numeradores juntos y luego multiplicar los denominadores juntos. Reducir si es necesario.

$\dfrac{\text{numerator 1}}{\text{denominator 1}} \cdot \dfrac{\text{numerator 2}}{\text{denominator 2}} = \dfrac{\text{numerator 1}}{\text{denominator 1}} \cdot \dfrac{\text{numerator 2}}{\text{denominator 2}}$

Conjunto de Muestras A

Realiza las siguientes multiplicaciones.

$\dfrac{3}{4} \cdot \dfrac{1}{6} = \dfrac{3 \cdot 1}{4 \cdot 6} = \dfrac{3}{24}$Ahora, reducir,

$= \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{24}} \\ {^{8}} \end{array}} = \dfrac{1}{8}$

Así

$\dfrac{3}{4} \cdot \dfrac{1}{6} = \dfrac{1}{8}$

Esto quiere decir que$\dfrac{3}{4}$ de$\dfrac{1}{6}$ es$\dfrac{1}{8}$, es decir,$\dfrac{3}{4}$$\dfrac{1}{6}$ de una unidad es$\dfrac{1}{8}$ de la unidad original.

Conjunto de Muestras A

$\dfrac{3}{8} \cdot 4$. Escribe 4 como una fracción escribiendo$\dfrac{4}{1}$

$\dfrac{3}{8} \cdot \dfrac{4}{1} = \dfrac{3 \cdot 4}{8 \cdot 1} = \dfrac{12}{8} = \dfrac{\begin{array} {c} {^3} \\ {\cancel{12}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} = \dfrac{3}{2}$

$\dfrac{3}{8} \cdot 4 = \dfrac{3}{2}$

Esto significa que$\dfrac{3}{8}$ de 4 unidades enteras es$\dfrac{3}{2}$ de una unidad entera.

Conjunto de Muestras A

$\dfrac{2}{5} \cdot \dfrac{5}{8} \cdot \dfrac{1}{4} = \dfrac{2 \cdot 5 \cdot 1}{5 \cdot 8 \cdot 4} = \dfrac{\begin{array} {c} {^1} \\ {\cancel{10}} \end{array}}{\begin{array} {c} {\cancel{160}} \\ {^{16}} \end{array}} = \dfrac{1}{16}$

Esto significa que$\dfrac{2}{5}$ de$\dfrac{5}{8}$$\dfrac{1}{4}$ de una unidad entera es$\dfrac{1}{16}$ de la unidad original.

Conjunto de práctica A

Realiza las siguientes multiplicaciones.

$\dfrac{2}{5} \cdot \dfrac{1}{6}$

Responder: $\dfrac{1}{15}$

Conjunto de práctica A

$\dfrac{1}{4} \cdot \dfrac{8}{9}$

Responder: $\dfrac{2}{9}$

Conjunto de práctica A

$\dfrac{4}{9} \cdot \dfrac{15}{16}$

Responder: $\dfrac{5}{12}$

Conjunto de práctica A

$(\dfrac{2}{3}) (\dfrac{2}{3})$

Responder: $\dfrac{4}{9}$

Conjunto de práctica A

$(\dfrac{7}{4}) (\dfrac{8}{5})$

Responder: $\dfrac{14}{5}$

Conjunto de práctica A

$\dfrac{5}{6} \cdot \dfrac{7}{8}$

Responder: $\dfrac{35}{48}$

Conjunto de práctica A

$\dfrac{2}{3} \cdot 5$

Responder: $\dfrac{10}{3}$

Conjunto de práctica A

$(\dfrac{3}{10}) (10)$

Responder: $\dfrac{15}{2}$

Conjunto de práctica A

$\dfrac{3}{4} \cdot \dfrac{8}{9} \cdot \dfrac{5}{12}$

Responder: $\dfrac{5}{18}$

Multiplicar fracciones dividiendo factores comunes

Hemos visto que para multiplicar dos fracciones juntas, multiplicamos numeradores juntos, luego denominadores juntos, luego reducimos a términos más bajos, si es necesario. La reducción puede ser tediosa si los números en las fracciones son grandes. Por ejemplo,

$\dfrac{9}{16} \cdot \dfrac{10}{21} = \dfrac{9 \cdot 10}{16 \cdot 21} = \dfrac{90}{336} = \dfrac{45}{168} = \dfrac{15}{28}$

Evitamos el proceso de reducción si dividimos los factores comunes antes de multiplicarnos.

$\dfrac{9}{16} \cdot \dfrac{10}{21} = \dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{16}} \\ {^8} \end{array}} \cdot \dfrac{\begin{array} {c} {^5} \\ {\cancel{10}} \end{array}}{\begin{array} {c} {\cancel{21}} \\ {^7} \end{array}} = \dfrac{3 \cdot 5}{8 \cdot 7} = \dfrac{15}{56}$

Divide 3 en 9 y 21, y divide 2 en 10 y 16. El producto es una fracción que se reduce a los términos más bajos.

Cómo: El proceso de multiplicación dividiendo factores comunes

Para multiplicar fracciones dividiendo factores comunes, divida los factores que son comunes tanto a un numerador como a un denominador. El factor que se divide puede aparecer en cualquier numerador y en cualquier denominador.

Conjunto de Muestras A

Realiza las siguientes multiplicaciones.

$\dfrac{4}{5} \cdot \dfrac{5}{6}$

$\dfrac{\begin{array} {c} {^2} \\ {\cancel{4}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{5}} \end{array}}{\begin{array} {c} {\cancel{6}} \\ {^1} \end{array}} = \dfrac{2 \cdot 1}{1 \cdot 3} = \dfrac{2}{3}$

Divide 4 y 6 por 2
Divide 5 y 5 por 5

Conjunto de Muestras A

$\dfrac{8}{12} \cdot \dfrac{8}{10}$

$\dfrac{\begin{array} {c} {^4} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{12}} \\ {^3} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{10}} \\ {^5} \end{array}} = \dfrac{4 \cdot 2}{3 \cdot 5} = \dfrac{8}{15}$

Divide 8 y 10 por 2.
Divide 8 y 12 por 4.

Conjunto de Muestras A

$8 \cdot \dfrac{5}{12} = \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{1} \cdot \dfrac{5}{\begin{array} {c} {\cancel{12}} \\ {^3} \end{array}} = \dfrac{2 \cdot 5}{1 \cdot 3} = \dfrac{10}{3}$

Conjunto de Muestras A

$\dfrac{35}{18} \cdot \dfrac{63}{105}$

$\dfrac{\begin{array} {c} {^{^1}} \\ {^{\cancel{7}}} \\ {\cancel{35}} \end{array}}{\begin{array} {c} {\cancel{18}} \\ {^2} \end{array}} \dfrac{\begin{array} {c} {^7} \\ {\cancel{63}} \end{array}}{\begin{array} {c} {\cancel{105}} \\ {^{\cancel{21}}} \\ {^{^3}} \end{array}} = \dfrac{1 \cdot 7}{2 \cdot 3} = \dfrac{7}{6}$

Conjunto de Muestras A

$\dfrac{13}{9} \cdot \dfrac{6}{39} \cdot \dfrac{1}{12}$

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{13}} \end{array}}{9} \cdot \dfrac{\begin{array} {c} {^{^1}} \\ {^{\cancel{2}}} \\ {\cancel{6}} \end{array}}{\begin{array} {c} {\cancel{39}} \\ {^{\cancel{3}}} \\ {^{^1}} \end{array}} \cdot \dfrac{1}{\begin{array} {c} {\cancel{12}} \\ {^6} \end{array}} = \dfrac{1 \cdot 1 \cdot 1}{9 \cdot 1 \cdot 6} = \dfrac{1}{54}$

Set de práctica B

Realiza las siguientes multiplicaciones.

$\dfrac{2}{3} \cdot \dfrac{7}{8}$

Responder: $\dfrac{7}{12}$

Set de práctica B

$\dfrac{25}{12} \cdot \dfrac{10}{45}$

Responder: $\dfrac{25}{54}$

Set de práctica B

$\dfrac{40}{48} \cdot \dfrac{72}{90}$

Responder: $\dfrac{2}{3}$

Set de práctica B

$7 \cdot \dfrac{2}{49}$

Responder: $\dfrac{2}{7}$

Set de práctica B

$12 \cdot \dfrac{3}{8}$

Responder: $\dfrac{9}{2}$

Set de práctica B

$(\dfrac{13}{7}) (\dfrac{14}{26})$

Responder: 1

Set de práctica B

$\dfrac{16}{10} \cdot \dfrac{22}{6} \cdot \dfrac{21}{44}$

Responder: $\dfrac{14}{5}$

Multiplicación de números mixtos

Multiplicar números mixtos
Para realizar una multiplicación en la que haya números mixtos, es conveniente convertir primero cada número mixto a una fracción impropia, luego multiplicar.

Conjunto de Muestras C

Realiza las siguientes multiplicaciones. Convertir fracciones impropias a números mixtos.

$1 \dfrac{1}{8} \cdot 4 \dfrac{2}{3}$

Convierte cada número mixto en una fracción impropia.

$1 \dfrac{1}{8} = \dfrac{8 \cdot 1 + 1}{8} = \dfrac{9}{8}$

$4 \dfrac{2}{3} = \dfrac{4 \cdot 3 + 2}{3} = \dfrac{14}{3}$

$\dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^4} \end{array}} \cdot \dfrac{\begin{array} {c} {^7} \\ {\cancel{14}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}} = \dfrac{3 \cdot 7}{4 \cdot 1} = \dfrac{21}{4} = 5 \dfrac{1}{4}$

Conjunto de Muestras C

$16 \cdot 8 \dfrac{1}{5}$

Convertir$8 \dfrac{1}{5}$ a una fracción impropia.

$8 \dfrac{1}{5} = \dfrac{5 \cdot 8 + 1}{5} = \dfrac{41}{5}$

$\dfrac{16}{1} \cdot \dfrac{41}{5}$.

No hay factores comunes para dividir.

$\dfrac{16}{1} \cdot \dfrac{41}{5} = \dfrac{16 \cdot 41}{1 \cdot 5} = \dfrac{656}{5} = 131 \dfrac{1}{5}$

Conjunto de Muestras C

$9 \dfrac{1}{6} \cdot 12 \dfrac{3}{5}$

Convertir a fracciones impropias.

$9 \dfrac{1}{6} = \dfrac{6 \cdot 9 + 1}{6} = \dfrac{55}{6}$

$12 \dfrac{3}{5} = \dfrac{5 \cdot 12 + 3}{5} = \dfrac{63}{5}$

$\dfrac{\begin{array} {c} {^{11}} \\ {\cancel{55}} \end{array}}{\begin{array} {c} {\cancel{6}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^{21}} \\ {\cancel{63}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} = \dfrac{11 \cdot 21}{2 \cdot 1} = \dfrac{231}{2} = 115 \dfrac{1}{2}$

Conjunto de Muestras C

$\begin{array} {rcl} {\dfrac{11}{8} \cdot 4 \dfrac{1}{2} \cdot 3 \dfrac{1}{8}} & = & {\dfrac{11}{8} \cdot \dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{2}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^5} \\ {\cancel{10}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{11 \cdot 3 \cdot 5}{8 \cdot 1 \cdot 1} = \dfrac{165}{8} = 20 \dfrac{5}{8}} \end{array}$

Set de práctica C

Realiza las siguientes multiplicaciones. Convertir fracciones impropias a números mixtos.

$2 \dfrac{2}{3} \cdot 2 \dfrac{1}{4}$

Responder: 6

Set de práctica C

$6 \dfrac{2}{3} \cdot 3 \dfrac{3}{10}$

Responder: 22

Set de práctica C

$7 \dfrac{1}{8} \cdot 12$

Responder: $85\dfrac{1}{2}$

Set de práctica C

$2 \dfrac{2}{5} \cdot 3 \dfrac{3}{4} \cdot 3 \dfrac{1}{3}$

Responder: 30

Poderes y Raíces de Fracciones

Conjunto de Muestras D

Encuentra el valor de cada uno de los siguientes.

$(\dfrac{1}{6})^2 = \dfrac{1}{6} \cdot \dfrac{1}{6} = \dfrac{1 \cdot 1}{6 \cdot 6} = \dfrac{1}{36}$

Conjunto de Muestras D

$\sqrt{\dfrac{9}{100}}$. Buscamos un número, ¿lo llamas? , de tal manera que cuando se encuentra al cuadrado,$\dfrac{9}{100}$ se produce.

$(?)^2 = \dfrac{9}{100}$

Sabemos que

$3^2 = 9$y$10^2 = 100$

Lo intentaremos$\dfrac{3}{10}$. Desde

$(\dfrac{3}{10})^2 = \dfrac{3}{10} \cdot \dfrac{3}{10} = \dfrac{3 \cdot 3}{10 \cdot 10} = \dfrac{9}{100}$

$\sqrt{\dfrac{9}{100}} = \dfrac{3}{10}$

Conjunto de Muestras D

$4\dfrac{2}{5} \cdot \sqrt{\dfrac{100}{121}}$

$\dfrac{\begin{array} {c} {^2} \\ {\cancel{22}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} \cdot \dfrac{^2}{\cancel{10}} = \dfrac{\begin{array} {c} {\cancel{11}} \\ {^1} \end{array}}{\begin{array} {c} {} \\ {} \end{array}} = \dfrac{4}{1} = 4$

$4 \dfrac{2}{5} \cdot \sqrt{\dfrac{100}{121}} = 4$

Set de Práctica D

Encuentra el valor de cada uno de los siguientes.

$(\dfrac{1}{8})^2$

Responder: $\dfrac{1}{64}$

Set de Práctica D

$(\dfrac{3}{10})^2$

Responder: $\dfrac{9}{100}$

Set de Práctica D

$\sqrt{\dfrac{4}{9}}$

Responder: $\dfrac{2}{3}$

Set de Práctica D

$\sqrt{\dfrac{1}{4}}$

Responder: $\dfrac{1}{2}$

Set de Práctica D

$\dfrac{3}{8} \cdot \sqrt{\dfrac{1}{9}}$

Responder: $\dfrac{1}{8}$

Set de Práctica D

$9 \dfrac{1}{3} \cdot \sqrt{\dfrac{81}{100}}$

Responder: $8 \dfrac{2}{5}$

Set de Práctica D

$2 \dfrac{8}{13} \cdot \sqrt{\dfrac{169}{16}}$

Responder: $8 \dfrac{1}{2}$

Ejercicios

Para los siguientes seis problemas, utilice los diagramas para encontrar cada una de las siguientes partes. Usa la multiplicación para verificar tu resultado.

Ejercicio$\PageIndex{1}$

$\dfrac{3}{4}$de$\dfrac{1}{3}$

$Un rectángulo dividido en doce partes en un patrón de cuatro filas y tres columnas.$

Responder

$\dfrac{1}{4}$

$Un rectángulo dividido en doce partes en un patrón de cuatro filas y tres columnas. Tres de las partes están sombreadas.$

Ejercicio$\PageIndex{2}$

$\dfrac{2}{3}$de$\dfrac{3}{5}$

$Un rectángulo dividido en doce partes en un patrón de tres filas y cuatro columnas.$

Ejercicio$\PageIndex{3}$

$\dfrac{2}{7}$de$\dfrac{7}{8}$

$Un rectángulo dividido en cincuenta y seis partes en un patrón de siete filas y ocho columnas.$

Responder

$\dfrac{1}{4}$

$Un rectángulo dividido en cincuenta y seis partes en un patrón de siete filas y ocho columnas. Catorce de las partes están sombreadas.$

Ejercicio$\PageIndex{4}$

$\dfrac{5}{6}$de$\dfrac{3}{4}$

$Un rectángulo dividido en veinticuatro partes en un patrón de seis filas y cuatro columnas.$

Ejercicio$\PageIndex{5}$

$\dfrac{1}{8}$de$\dfrac{1}{8}$

$Un rectángulo dividido en sesenta y cuatro partes en un patrón de ocho filas y ocho columnas.$

Responder

$\dfrac{1}{64}$

$Un rectángulo dividido en sesenta y cuatro partes en un patrón de ocho filas y ocho columnas. Una parte está sombreada.$

Ejercicio$\PageIndex{6}$

$\dfrac{7}{12}$de$\dfrac{6}{7}$

$Un rectángulo dividido en ochenta y cuatro partes en un patrón de doce filas y siete columnas.$

Para los siguientes problemas, encuentra cada parte sin usar un diagrama.

Ejercicio$\PageIndex{7}$

$\dfrac{1}{2}$de$\dfrac{4}{5}$

Responder: $\dfrac{2}{5}$

Ejercicio$\PageIndex{8}$

$\dfrac{3}{5}$de$\dfrac{5}{12}$

Ejercicio$\PageIndex{9}$

$\dfrac{1}{4}$de$\dfrac{8}{9}$

Responder: $\dfrac{2}{9}$

Ejercicio$\PageIndex{10}$

$\dfrac{3}{16}$de$\dfrac{12}{15}$

Ejercicio$\PageIndex{11}$

$\dfrac{2}{9}$de$\dfrac{6}{5}$

Responder: $\dfrac{4}{15}$

Ejercicio$\PageIndex{12}$

$\dfrac{1}{8}$de$\dfrac{3}{8}$

Ejercicio$\PageIndex{13}$

$\dfrac{2}{3}$de$\dfrac{9}{10}$

Responder: $\dfrac{3}{5}$

Ejercicio$\PageIndex{14}$

$\dfrac{18}{19}$de$\dfrac{38}{54}$

Ejercicio$\PageIndex{15}$

$\dfrac{5}{6}$de$2 \dfrac{2}{5}$

Responder: 2

Ejercicio$\PageIndex{16}$

$\dfrac{3}{4}$de$3 \dfrac{3}{5}$

Ejercicio$\PageIndex{17}$

$\dfrac{3}{2}$de$2 \dfrac{2}{9}$

Responder: $\dfrac{10}{3}$o$3 \dfrac{1}{3}$

Ejercicio$\PageIndex{18}$

$\dfrac{15}{4}$de$4 \dfrac{4}{5}$

Ejercicio$\PageIndex{19}$

$5 \dfrac{1}{3}$de$9 \dfrac{3}{4}$

Responder: 52

Ejercicio$\PageIndex{20}$

$1 \dfrac{13}{15}$de$8 \dfrac{3}{4}$

Ejercicio$\PageIndex{21}$

$\dfrac{8}{9}$$\dfrac{3}{4}$de$\dfrac{2}{3}$

Responder: $\dfrac{4}{9}$

Ejercicio$\PageIndex{22}$

$\dfrac{1}{6}$$\dfrac{12}{13}$de$\dfrac{26}{36}$

Ejercicio$\PageIndex{23}$

$\dfrac{1}{2}$$\dfrac{1}{3}$de$\dfrac{1}{4}$

Responder: $\dfrac{1}{24}$

Ejercicio$\PageIndex{24}$

$1 \dfrac{3}{7}$$5 \dfrac{1}{5}$de$8 \dfrac{1}{3}$

Ejercicio$\PageIndex{25}$

$2 \dfrac{4}{5}$$5 \dfrac{5}{6}$de$7 \dfrac{5}{7}$

Responder: 126

Para los siguientes problemas, encuentra los productos. Asegúrate de reducir.

Ejercicio$\PageIndex{26}$

$\dfrac{1}{3} \cdot \dfrac{2}{3}$

Ejercicio$\PageIndex{27}$

$\dfrac{1}{2} \cdot \dfrac{1}{2}$

Responder: $\dfrac{1}{4}$

Ejercicio$\PageIndex{28}$

$\dfrac{3}{4} \cdot \dfrac{3}{8}$

Ejercicio$\PageIndex{29}$

$\dfrac{2}{5} \cdot \dfrac{5}{6}$

Responder: $\dfrac{1}{3}$

Ejercicio$\PageIndex{30}$

$\dfrac{3}{8} \cdot \dfrac{8}{9}$

Ejercicio$\PageIndex{31}$

$\dfrac{5}{6} \cdot \dfrac{14}{15}$

Responder: $\dfrac{7}{9}$

Ejercicio$\PageIndex{32}$

$\dfrac{4}{7} \cdot \dfrac{7}{4}$

Ejercicio$\PageIndex{33}$

$\dfrac{3}{11} \cdot \dfrac{11}{3}$

Responder: 1

Ejercicio$\PageIndex{34}$

$\dfrac{9}{16} \cdot \dfrac{20}{27}$

Ejercicio$\PageIndex{35}$

$\dfrac{35}{36} \cdot \dfrac{48}{55}$

Responder: $\dfrac{28}{33}$

Ejercicio$\PageIndex{36}$

$\dfrac{21}{25} \cdot \dfrac{15}{14}$

Ejercicio$\PageIndex{37}$

$\dfrac{76}{99} \cdot \dfrac{66}{38}$

Responder: $\dfrac{4}{3}$

Ejercicio$\PageIndex{38}$

$\dfrac{3}{7} \cdot \dfrac{14}{18} \cdot \dfrac{6}{2}$

Ejercicio$\PageIndex{39}$

$\dfrac{4}{15} \cdot \dfrac{10}{3} \cdot \dfrac{27}{2}$

Responder: 12

Ejercicio$\PageIndex{40}$

$\dfrac{14}{15} \cdot \dfrac{21}{28} \cdot \dfrac{45}{7}$

Ejercicio$\PageIndex{41}$

$\dfrac{8}{3} \cdot \dfrac{15}{4} \cdot \dfrac{16}{21}$

Responder: $7\dfrac{13}{21}$o$\dfrac{160}{21}$

Ejercicio$\PageIndex{42}$

$\dfrac{18}{14} \cdot \dfrac{21}{35} \cdot \dfrac{36}{7}$

Ejercicio$\PageIndex{43}$

$\dfrac{3}{5} \cdot 20$

Responder: 12

Ejercicio$\PageIndex{44}$

$\dfrac{8}{9} \cdot 18$

Ejercicio$\PageIndex{45}$

$\dfrac{6}{11} \cdot 33$

Responder: 18

Ejercicio$\PageIndex{46}$

$\dfrac{18}{19} \cdot 38$

Ejercicio$\PageIndex{47}$

$\dfrac{5}{6} \cdot 10$

Responder: $\dfrac{25}{3}$o$8\dfrac{1}{3}$

Ejercicio$\PageIndex{48}$

$\dfrac{1}{9} \cdot 3$

Ejercicio$\PageIndex{49}$

$5 \cdot \dfrac{3}{8}$

Responder: $\dfrac{15}{8} =1 \dfrac{7}{8}$

Ejercicio$\PageIndex{50}$

$16 \cdot \dfrac{1}{4}$

Ejercicio$\PageIndex{51}$

$\dfrac{2}{3} \cdot 12 \cdot \dfrac{3}{4}$

Responder: 6

Ejercicio$\PageIndex{52}$

$\dfrac{3}{8} \cdot 24 \cdot \dfrac{2}{3}$

Ejercicio$\PageIndex{53}$

$\dfrac{5}{18} \cdot 10 \cdot \dfrac{2}{5}$

Responder: $\dfrac{10}{9} = 1 \dfrac{1}{9}$

Ejercicio$\PageIndex{54}$

$\dfrac{16}{15} \cdot 50 \cdot \dfrac{3}{10}$

Ejercicio$\PageIndex{55}$

$5 \dfrac{1}{3} \cdot \dfrac{27}{32}$

Responder: $\dfrac{9}{2} = 4 \drac{1}{2}$

Ejercicio$\PageIndex{56}$

$2 \dfrac{6}{7} \cdot 5 \dfrac{3}{5}$

Ejercicio$\PageIndex{57}$

$6 \dfrac{1}{4} \cdot 2 \dfrac{4}{15}$

Responder: $\dfrac{85}{6} = 14 \drac{1}{6}$

Ejercicio$\PageIndex{58}$

$9\dfrac{1}{3} \cdot \dfrac{9}{16} \cdot 1 \dfrac{1}{3}$

Ejercicio$\PageIndex{59}$

$3 \dfrac{5}{9} \cdot 1 \dfrac{13}{14} \cdot 10 \dfrac{1}{2}$

Responder: 72

Ejercicio$\PageIndex{60}$

$20 \dfrac{1}{4} \cdot 8 \dfrac{2}{3} \cdot 16 \dfrac{4}{5}$

Ejercicio$\PageIndex{61}$

$(\dfrac{2}{3})^2$

Responder: $\dfrac{4}{9}$

Ejercicio$\PageIndex{62}$

$(\dfrac{3}{8})^2$

Ejercicio$\PageIndex{63}$

$(\dfrac{2}{11})^2$

Responder: $\dfrac{4}{121}$

Ejercicio$\PageIndex{64}$

$(\dfrac{8}{9})^2$

Ejercicio$\PageIndex{65}$

$(\dfrac{1}{2})^2$

Responder: $\dfrac{1}{4}$

Ejercicio$\PageIndex{66}$

$(\dfrac{3}{5})^2 \cdot \dfrac{20}{3}$

Ejercicio$\PageIndex{67}$

$(\dfrac{1}{4})^2 \cdot \dfrac{16}{15}$

Responder: $\dfrac{1}{15}$

Ejercicio$\PageIndex{68}$

$(\dfrac{1}{2})^2 \cdot \dfrac{8}{9}$

Ejercicio$\PageIndex{69}$

$(\dfrac{1}{2})^2 \cdot (\dfrac{2}{5})^2$

Responder: $\dfrac{1}{25}$

Ejercicio$\PageIndex{70}$

$(\dfrac{3}{7})^2 \cdot (\dfrac{1}{9})^2$

Para los siguientes problemas, encuentra cada valor. Reduzca las respuestas a los términos más bajos o convierta a números mixtos.

Ejercicio$\PageIndex{71}$

$\sqrt{\dfrac{4}{9}}$

Responder: $\dfrac{2}{3}$

Ejercicio$\PageIndex{72}$

$\sqrt{\dfrac{16}{25}}$

Ejercicio$\PageIndex{73}$

$\sqrt{\dfrac{81}{121}}$

Responder: $\dfrac{9}{11}$

Ejercicio$\PageIndex{74}$

$\sqrt{\dfrac{36}{49}}$

Ejercicio$\PageIndex{75}$

$\sqrt{\dfrac{144}{25}}$

Responder: $\dfrac{12}{5} = 2 \dfrac{2}{5}$

Ejercicio$\PageIndex{76}$

$\dfrac{2}{3} \cdot \sqrt{\dfrac{9}{16}}$

Ejercicio$\PageIndex{77}$

$\dfrac{3}{5} \cdot \sqrt{\dfrac{25}{81}}$

Responder: $\dfrac{1}{3}$

Ejercicio$\PageIndex{78}$

$(\dfrac{8}{5})^2 \cdot \sqrt{\dfrac{25}{64}}$

Ejercicio$\PageIndex{79}$

$(1 \dfrac{3}{4})^2 \cdot \sqrt{\dfrac{4}{49}}$

Responder: $\dfrac{7}{8}$

Ejercicio$\PageIndex{80}$

$(2 \dfrac{2}{3})^2 \cdot \sqrt{\dfrac{36}{49}} \cdot \sqrt{\dfrac{64}{81}}$

Ejercicios para revisión

Ejercicio$\PageIndex{81}$

¿Cuántos miles hay 342.810?

Responder: 2

Ejercicio$\PageIndex{82}$

Encuentra la suma de 22, 42 y 101.

Ejercicio$\PageIndex{83}$

¿Es 634.281 divisible por 3?

Responder: si

Ejercicio$\PageIndex{84}$

¿Es el número entero 51 primo o compuesto?

Ejercicio$\PageIndex{85}$

Reducir$\dfrac{36}{150}$ a los términos más bajos

Responder: $\dfrac{6}{25}$