4.5: División de Fracciones

Última actualización
Guardar como PDF

Page ID: 116735

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de determinar el recíproco de un número
ser capaz de dividir una fracción por otra

Reciprocales

Definición: Reciprocales

Dos números cuyo producto es 1 se denominan recíprocos entre sí.

Conjunto de Muestras A

Los siguientes pares de números son recíprocos.

$\underbrace{\dfrac{3}{4} \text{and} \dfrac{4}{3}}_{\dfrac{3}{4} \cdot \dfrac{4}{3} = 1}$

Conjunto de Muestras A

$\underbrace{\dfrac{7}{16} \text{and} \dfrac{16}{7}}_{\dfrac{7}{16} \cdot \dfrac{16}{7} = 1}$

Conjunto de Muestras A

$\underbrace{\dfrac{1}{6} \text{and} \dfrac{6}{1}}_{\dfrac{1}{6} \cdot \dfrac{6}{1} = 1}$

Observe que podemos encontrar el recíproco de un número distinto de cero en forma fraccionaria al invertirlo (intercambiando posiciones del numerador y denominador).

Conjunto de práctica A

Encuentra el recíproco de cada número.

$\dfrac{3}{10}$

Contestar: $\dfrac{10}{3}$

Conjunto de práctica A

$\dfrac{2}{3}$

Contestar: $\dfrac{3}{2}$

Conjunto de práctica A

$\dfrac{7}{8}$

Contestar: $\dfrac{8}{7}$

Conjunto de práctica A

$\dfrac{1}{5}$

Contestar: 5

Conjunto de práctica A

$2 \dfrac{2}{7}$

Pista

Escribe primero este número como una fracción impropia.

Contestar: $\dfrac{7}{16}$

Conjunto de práctica A

$5 \dfrac{1}{4}$

Contestar: $\dfrac{4}{21}$

Conjunto de práctica A

$10 \dfrac{3}{16}$

Contestar: $\dfrac{16}{163}$

Dividiendo Fracciones

Nuestro concepto de división es que indica cuántas veces una cantidad está contenida en otra cantidad. Por ejemplo, usando el diagrama podemos ver que hay 6 un tercio en 2.

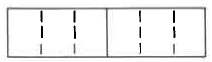
$Dos rectángulos, cada uno dividido en tres partes. Los rectángulos están conectados entre sí.$

Hay 6 un tercio en 2.

Dado que 2 contiene seis$\dfrac{1}{3}$, expresamos esto como

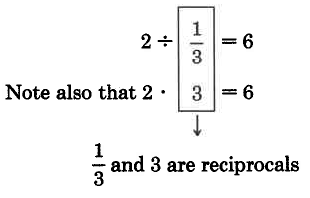
$Dos divididos por un tercio es igual a seis. Obsérvese también que dos por tres es igual a seis, porque un tercio y tres son recíprocos.$

Usando estas observaciones, podemos sugerir el siguiente método para dividir un número por una fracción.

Dividiendo Una Fracción por Otra Fracción
Para dividir una primera fracción por una segunda fracción distinta de cero, multiplique la primera tracción por el recíproco de la segunda fracción.

Invertir y Multiplicar
Este método se conoce comúnmente como “invertir el divisor y multiplicar”.

Conjunto de Muestras B

Realizar las siguientes divisiones.

$\dfrac{1}{2} \div \dfrac{3}{4}$. El divisor es$\dfrac{3}{4}$. Su recíproco es$\dfrac{4}{3}$. Multiplicar$\dfrac{1}{3}$ por$\dfrac{4}{3}$.

$\dfrac{1}{3} \cdot \dfrac{4}{3} = \dfrac{1 \cdot 4}{3 \cdot 3} = \dfrac{4}{9}$

$\dfrac{1}{2} \div \dfrac{3}{4} = \dfrac{4}{9}$

Conjunto de Muestras B

$\dfrac{3}{8} \div \dfrac{5}{4}$. El divisor es$\dfrac{5}{4}$. Su recíproco es$\dfrac{4}{5}$. Multiplicar$\dfrac{3}{8}$ por$\dfrac{4}{5}$.

$\dfrac{3}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{4}} \end{array}}{5} = \dfrac{3 \cdot 1}{2 \cdot 5} = \dfrac{3}{10}$

$\dfrac{3}{8} \div \dfrac{5}{4} = \dfrac{3}{10}$

Conjunto de Muestras B

$\dfrac{5}{6} \div \dfrac{5}{12}$. El divisor es$\dfrac{5}{12}$. Su recíproco es$\dfrac{12}{5}$. Multiplicar$\dfrac{5}{6}$ por$\dfrac{12}{5}$.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{5}} \end{array}}{\begin{array} {c} {\cancel{6}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{12}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} = \dfrac{1 \cdot 2}{1 \cdot 1} = \dfrac{2}{1} = 2$

$\dfrac{5}{6} \div \dfrac{5}{12} = 2$

Conjunto de Muestras B

$2 \dfrac{2}{9} \div 3 \dfrac{1}{3}$. Convierte cada número mixto en una fracción impropia.

$2 \dfrac{2}{9} = \dfrac{9 \cdot 2 + 2}{9} = \dfrac{20}{9}$.

$3 \dfrac{1}{3} = \dfrac{3 \cdot 3 + 1}{3} = \dfrac{10}{3}$.

$\dfrac{20}{9} \div \dfrac{10}{3}$El divisor es$\dfrac{10}{3}$. Su recíproco es$\dfrac{3}{10}$. Multiplicar$\dfrac{20}{9}$ por$\dfrac{3}{10}$.

$\dfrac{\begin{array} {c} {^2} \\ {\cancel{20}} \end{array}}{\begin{array} {c} {\cancel{9}} \\ {^3} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{10}} \\ {^1} \end{array}} = \dfrac{2 \cdot 1}{3 \cdot 1} = \dfrac{2}{3}$

$2 \dfrac{2}{9} \div 3 \dfrac{1}{3} = \dfrac{2}{3}$

Conjunto de Muestras B

$\dfrac{12}{11} \div 8$. Primero convenientemente escriba 8 como$\dfrac{8}{1}$.

$\dfrac{12}{11} \div \dfrac{8}{1}$. El divisor es$\dfrac{8}{1}$. Su recíproco es$\dfrac{1}{8}$. Multiplicar$\dfrac{12}{11}$ por$\dfrac{1}{8}$.

$\dfrac{\begin{array} {c} {^3} \\ {\cancel{12}} \end{array}}{11} \cdot \dfrac{1}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} = \dfrac{3 \cdot 1}{11 \cdot 2} = \dfrac{3}{22}$

$\dfrac{12}{11} \div 8 = \dfrac{3}{22}$

Conjunto de Muestras B

$\dfrac{7}{8} \div \dfrac{21}{20} \cdot \dfrac{3}{35}$. El divisor es$\dfrac{21}{20}$. Su recíproco es$\dfrac{20}{21}$.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{7}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^{^1}} \\ {^{\cancel{5}}} \\ {\cancel{20}} \end{array}}{\begin{array} {c} {\cancel{21}} \\ {^{\cancel{3}}} \\ {^{^1}} \end{array}} \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{35}} \\ {^7} \end{array}} = \dfrac{1 \cdot 1 \cdot 1}{2 \cdot 1 \cdot 7} = \dfrac{1}{14}$

$\dfrac{7}{8} \div \dfrac{21}{20} \cdot \dfrac{3}{25} = \dfrac{1}{14}$

Conjunto de Muestras B

¿Cuántos paquetes de$2 \dfrac{3}{8}$ pulgadas de ancho se pueden colocar en una caja de 19 pulgadas de ancho?

El problema es determinar cuántos dos y tres octavos están contenidos en 19, es decir, ¿qué es$19 \div 2 \dfrac{3}{8}$?

$2\dfrac{3}{8} = \dfrac{19}{8}$Convierte el divisor$2 \dfrac{3}{8}$ en una fracción impropia.

$19 = \dfrac{19}{1}$Escribe el dividendo 19 como$\dfrac{19}{1}$.

$\dfrac{19}{1} \div \dfrac{19}{8}$El divisor es$\dfrac{19}{8}$. Su recíproco es$\dfrac{8}{19}$.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{19}} \end{array}}{1} \cdot \dfrac{8}{\begin{array} {c} {\cancel{19}} \\ {^1} \end{array}} = \dfrac{1 \cdot 8}{1 \cdot 1} = \dfrac{8}{1} = 8$

De esta manera, cabrán 8 paquetes en la caja.

Set de práctica B

Realizar las siguientes divisiones.

$\dfrac{1}{2} \div \dfrac{9}{8}$

Contestar: $\dfrac{4}{9}$

Set de práctica B

$\dfrac{3}{8} \div \dfrac{9}{24}$

Contestar: 1

Set de práctica B

$\dfrac{7}{15} \div \dfrac{14}{15}$

Contestar: $\dfrac{1}{2}$

Set de práctica B

$8 \div \dfrac{8}{15}$

Contestar: 15

Set de práctica B

$6 \dfrac{1}{4} \div \dfrac{5}{12}$

Contestar: 15

Set de práctica B

$3 \dfrac{1}{3} \div 1 \dfrac{2}{3}$

Contestar: 2

Set de práctica B

$\dfrac{5}{6} \div \dfrac{2}{3} \cdot \dfrac{8}{25}$

Contestar: $\dfrac{2}{5}$

Set de práctica B

Un recipiente contendrá 106 onzas de jugo de uva. ¿Cuántos vasos de$6 \dfrac{5}{8}$ -onza de jugo de uva se pueden servir de este recipiente?

Contestar: 16 vasos

Determine cada uno de los siguientes cocientes y luego escriba una regla para este tipo de división.

Set de práctica B

$1 \div \dfrac{2}{3}$

Contestar: $\dfrac{3}{2}$

Set de práctica B

$1 \div \dfrac{3}{8}$

Contestar: $\dfrac{8}{3}$

Set de práctica B

$1 \div \dfrac{3}{4}$

Contestar: $\dfrac{4}{3}$

Set de práctica B

$1 \div \dfrac{5}{2}$

Contestar: $\dfrac{2}{5}$

Set de práctica B

Al dividir 1 por una fracción, el cociente es el.

Contestar: es el recíproco de la fracción.

Ejercicios

Para los siguientes problemas, encuentra el recíproco de cada número.

Ejercicio$\PageIndex{1}$

$\dfrac{4}{5}$

Contestar: $\dfrac{5}{4}$o$1 \dfrac{1}{4}$

Ejercicio$\PageIndex{2}$

$\dfrac{8}{11}$

Ejercicio$\PageIndex{3}$

$\dfrac{2}{9}$

Contestar: $\dfrac{9}{2}$o$4 \dfrac{1}{2}$

Ejercicio$\PageIndex{4}$

$\dfrac{1}{5}$

Ejercicio$\PageIndex{5}$

$3\dfrac{1}{4}$

Contestar: $\dfrac{4}{13}$

Ejercicio$\PageIndex{6}$

$8 \dfrac{1}{4}$

Ejercicio$\PageIndex{7}$

$3\dfrac{2}{7}$

Contestar: $\dfrac{7}{23}$

Ejercicio$\PageIndex{8}$

$5 \dfrac{3}{4}$

Ejercicio$\PageIndex{9}$

Contestar: 1

Ejercicio$\PageIndex{10}$

Para los siguientes problemas, encuentra cada valor.

Ejercicio$\PageIndex{11}$

$\dfrac{3}{8} \div \dfrac{3}{5}$

Contestar: $\dfrac{5}{8}$

Ejercicio$\PageIndex{12}$

$\dfrac{5}{9} \div \dfrac{5}{6}$

Ejercicio$\PageIndex{13}$

$\dfrac{9}{16} \div \dfrac{15}{8}$

Contestar: $\dfrac{3}{10}$

Ejercicio$\PageIndex{14}$

$\dfrac{4}{9} \div \dfrac{6}{15}$

Ejercicio$\PageIndex{15}$

$\dfrac{25}{49} \div \dfrac{4}{9}$

Contestar: $\dfrac{225}{196}$o$1 \dfrac{29}{196}$

Ejercicio$\PageIndex{16}$

$\dfrac{15}{4} \div \dfrac{27}{8}$

Ejercicio$\PageIndex{17}$

$\dfrac{24}{75} \div \dfrac{8}{15}$

Contestar: $\dfrac{3}{5}$

Ejercicio$\PageIndex{18}$

$\dfrac{5}{7} \div 0$

Ejercicio$\PageIndex{19}$

$\dfrac{7}{8} \div \dfrac{7}{8}$

Contestar: 1

Ejercicio$\PageIndex{20}$

$0 \div \dfrac{3}{5}$

Ejercicio$\PageIndex{21}$

$\dfrac{4}{11} \div \dfrac{4}{11}$

Contestar: 1

Ejercicio$\PageIndex{22}$

$\dfrac{2}{3} \div \dfrac{2}{3}$

Ejercicio$\PageIndex{23}$

$\dfrac{7}{10} \div \dfrac{10}{7}$

Contestar: $\dfrac{49}{100}$

Ejercicio$\PageIndex{24}$

$\dfrac{3}{4} \div 6$

Ejercicio$\PageIndex{25}$

$\dfrac{9}{5} \div 3$

Contestar: $\dfrac{3}{5}$

Ejercicio$\PageIndex{26}$

$4 \dfrac{1}{6} \div 3 \dfrac{1}{3}$

Ejercicio$\PageIndex{27}$

$7 \dfrac{1}{7} \div 8 \dfrac{1}{3}$

Contestar: $\dfrac{6}{7}$

Ejercicio$\PageIndex{28}$

$1 \dfrac{1}{2} \div 1 \dfrac{1}{5}$

Ejercicio$\PageIndex{29}$

$3 \dfrac{2}{5} \div \dfrac{6}{25}$

Contestar: $\dfrac{85}{6}$o$14 \dfrac{1}{6}$

Ejercicio$\PageIndex{30}$

$5 \dfrac{1}{6} \div \dfrac{31}{6}$

Ejercicio$\PageIndex{31}$

$\dfrac{35}{6} \div 3 \dfrac{3}{4}$

Contestar: $\dfrac{28}{18} = \dfrac{14}{9}$o$1 \dfrac{5}{9}$

Ejercicio$\PageIndex{32}$

$5 \dfrac{1}{9} \div \dfrac{1}{18}$

Ejercicio$\PageIndex{33}$

$8 \dfrac{3}{4} \div \dfrac{7}{8}$

Contestar: 10

Ejercicio$\PageIndex{34}$

$\dfrac{12}{8} \div 1 \dfrac{1}{2}$

Ejercicio$\PageIndex{35}$

$3 \dfrac{1}{8} \div \dfrac{15}{16}$

Contestar: $\dfrac{10}{3}$o$3 \dfrac{1}{3}$

Ejercicio$\PageIndex{36}$

$11 \dfrac{11}{12} \div 9 \dfrac{5}{8}$

Ejercicio$\PageIndex{37}$

$2 \dfrac{2}{9} \div 11 \dfrac{2}{3}$

Contestar: $\dfrac{4}{21}$

Ejercicio$\PageIndex{38}$

$\dfrac{16}{3} \div 6 \dfrac{2}{5}$

Ejercicio$\PageIndex{39}$

$4 \dfrac{3}{25} \div 2 \dfrac{56}{75}$

Contestar: $\dfrac{3}{2}$o$1 \dfrac{1}{2}$

Ejercicio$\PageIndex{40}$

$\dfrac{1}{1000} \div \dfrac{1}{100}$

Ejercicio$\PageIndex{41}$

$\dfrac{3}{8} \div \dfrac{9}{16} \cdot \dfrac{6}{5}$

Contestar: $\dfrac{4}{5}$

Ejercicio$\PageIndex{42}$

$\dfrac{3}{16} \cdot \dfrac{9}{8} \cdot \dfrac{6}{5}$

Ejercicio$\PageIndex{43}$

$\dfrac{4}{15} \div \dfrac{2}{25} \cdot \dfrac{9}{10}$

Contestar: 3

Ejercicio$\PageIndex{44}$

$\dfrac{21}{30} \cdot 1 \dfrac{1}{4} \div \dfrac{9}{10}$

Ejercicio$\PageIndex{45}$

$8 \dfrac{1}{3} \cdot \dfrac{36}{75} \div 4$

Contestar: 1

Ejercicios para la revisión

Ejercicio$\PageIndex{46}$

¿Cuál es el valor de 5 en el número 504,216?

Ejercicio$\PageIndex{47}$

Encuentra el producto de 2,010 y 160.

Contestar: 321,600

Ejercicio$\PageIndex{48}$

Utilice los números 8 y 5 para ilustrar la propiedad conmutativa de la multiplicación.

Ejercicio$\PageIndex{49}$

Encuentra el múltiplo menos común de 6, 16 y 72.

Contestar: 144

Ejercicio$\PageIndex{50}$

Encuentra$\dfrac{8}{9}$ de$6 \dfrac{3}{4}$