Saltar al contenido principal
LibreTexts Español

9.2: El Sistema Métrico de Medición

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    116253

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje

    • estar más familiarizado con algunas de las ventajas del sistema de números base diez
    • conocer los prefijos de las medidas métricas
    • estar familiarizado con el sistema métrico de medición
    • ser capaz de convertir de una unidad de medida en el sistema métrico a otra unidad de medida

    Las ventajas del sistema de números base diez

    El sistema métrico de medición aprovecha nuestro sistema de números base diez. La ventaja del sistema métrico sobre el sistema de Estados Unidos es que en el sistema métrico es posible convertir de una unidad de medida a otra simplemente multiplicando o dividiendo el número dado por una potencia de 10. Esto significa que podemos hacer una conversión simplemente moviendo el punto decimal hacia la derecha o hacia la izquierda.

    Prefijos

    Las unidades de medida comunes en el sistema métrico son el metro (para la longitud), el litro (para el volumen) y el gramo (para la masa). A cada una de las unidades se le puede adjuntar un prefijo. Los prefijos métricos junto con su significado se enumeran a continuación.

    Prefijos métricos

    kilo: mil
    deci: décimo
    hecto: cien
    centi: centésima
    deka: diez
    milli: milésima

    Por ejemplo, si se está midiendo la longitud,

    1 kilómetro equivale a 1000 metros.
    1 centímetro equivale a una centésima de metro.
    1 milímetro equivale a una milésima de metro.

    Conversión de Una Unidad a Otra Unidad

    Anotemos tres características del sistema métrico que ocurren en la tabla métrica de medidas.

    1. En cada categoría, los prefijos son los mismos.
    2. Podemos pasar de una unidad de medida más grande a una más pequeña moviendo el punto decimal hacia la derecha.
    3. Podemos pasar de una unidad de medida más pequeña a otra más grande moviendo el punto decimal hacia la izquierda.

    En la siguiente tabla se proporciona un resumen de la relación entre la unidad de medida básica (metro, gramo, litro) y cada prefijo, y cuántos lugares se mueve el punto decimal y en qué dirección.

    kilo hecto deka unidad deci centi milli

    Unidad básica a prefijo Mover el punto decimal
    unidad a deka 1 a 10 1 lugar a la izquierda
    unidad a hector 1 a 100 2 lugares a la izquierda
    unidad a kilo 1 a 1,000 3 lugares a la izquierda
    unidad a deci 1 a 0.1 1 lugar a la derecha
    unidad a centi 1 a 0.01 2 lugares a la derecha
    unidad a milli 1 a 0.001 3 lugares a la derecha

    Tabla de conversión

    A continuación, en la tabla de conversión de unidades, se enumeran algunas de las unidades métricas de medida comunes.

    Tabla de conversión de unidades
    Largo \(\text{1 kilometer (km) = 1,000 meters } (m)\) \(1,000 \times 1\text{m}\)
    \(\text{1 hectometer (hm) = 100 meters}\) \(100 \times 1 \text{m}\)
    \(\text{1 dekameter (dam) = 10 meters}\) \(10 \times 1 \text{m}\)
    \(\text{1 meter (m)}\) \(1 \times 1 \text{m}\)
    \(\text{1 decimeter (dm) = } \dfrac{1}{10} \text{ meter}\) \(.1 \times 1 \text{m}\)
    \(\text{1 centimeter (cm) = } \dfrac{1}{100} \text{ meter}\) \(.01 \times 1 \text{m}\)
    \(\text{1 millimeter (mm) = } \dfrac{1}{1,000} \text{ meter}\) \(.001 \times 1 \text{m}\)
    Masa \(\text{1 kilogram (kg) = 1,000 grams } (g)\) \(1,000 \times 1\text{g}\)
    \(\text{1 hectogram (hg) = 100 grams}\) \(100 \times 1 \text{g}\)
    \(\text{1 dekagram (dag) = 10 grams}\) \(10 \times 1 \text{g}\)
    \(\text{1 gram (g)}\) \(1 \times 1 \text{g}\)
    \(\text{1 decigram (dg) = } \dfrac{1}{10} \text{ gram}\) \(.1 \times 1 \text{g}\)
    \(\text{1 centigram (cg) = } \dfrac{1}{100} \text{ gram}\) \(.01 \times 1 \text{g}\)
    \(\text{1 milligram (mg) = } \dfrac{1}{1,000} \text{ gram}\) \(.001 \times 1 \text{g}\)
    Volumen \(\text{1 kiloliter (kL) = 1,000 liters } (L)\) \(1,000 \times 1\text{L}\)
    \(\text{1 hectoliter (hL) = 100 liters}\) \(100 \times 1 \text{L}\)
    \(\text{1 dekaliter (daL) = 10 liters}\) \(10 \times 1 \text{L}\)
    \(\text{1 liter (L)}\) \(1 \times 1 \text{L}\)
    \(\text{1 deciliter (dL) = } \dfrac{1}{10} \text{ liter}\) \(.1 \times 1 \text{L}\)
    \(\text{1 centiliter (cL) = } \dfrac{1}{100} \text{ liter}\) \(.01 \times 1 \text{L}\)
    \(\text{1 milliliter (mL) = } \dfrac{1}{1,000} \text{ liter}\) \(.001 \times 1 \text{L}\)
    Tiempo Igual que el sistema de Estados Unidos

    Distinción entre masa y peso
    Existe una distinción entre masa y peso. El peso de un cuerpo está relacionado con la gravedad mientras que la masa de un cuerpo no lo está. Por ejemplo, tu peso en la tierra es diferente de lo que es en la luna, pero tu masa es la misma en ambos lugares. La masa es una medida de la resistencia de un cuerpo al movimiento. Cuanto más masivo es un cuerpo, más resistente es al movimiento. Además, los cuerpos más masivos pesan más que los cuerpos menos masivos.

    Convertir unidades métricas
    Para convertir de una unidad métrica a otra unidad métrica:

    1. Determine la ubicación del número original en la escala métrica (representado en cada uno de los siguientes ejemplos).
    2. Mueve el punto decimal del número original en la misma dirección y el mismo número de lugares que sea necesario para moverte a la unidad métrica a la que deseas ir.

    También podemos convertir de una unidad métrica a otra usando fracciones unitarias. Ambos métodos se muestran en el Conjunto de Muestras A.

    Conjunto de Muestras A

    Convierte 3 kilogramos en gramos.

    Solución

    a. 3 kg se pueden escribir como 3.0 kg. Entonces,
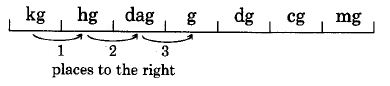
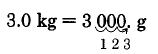
    Una línea con marcas hash dividiendo la línea en siete segmentos. Los segmentos están etiquetados, de izquierda a derecha, kg, hg, dag, g, dg, cg y mg. Por debajo de kg, hg, dagga y g hay flechas que apuntan desde cada segmento al segmento vecino a la derecha. Estas flechas están etiquetadas con 1, 2 y 3, indicando el número de lugares a la derecha.3.0 kg es igual a 3000g. Se dibuja una flecha debajo de los tres ceros en 3000, contando tres decimales a la derecha.

    Así,\(\text{3 kg = 3,000 g}\).

    b. También podemos usar fracciones unitarias para realizar esta conversión.

    Ya que estamos convirtiendo a gramos, y\(\text{1,000 g = 1 kg}\). elegimos la fracción unitaria\(\dfrac{\text{1,000 g}}{\text{1 kg}}\) ya que gramos está en el numerador.

    \(\begin{array} {rcl} {\text{3 kg}} & = & {\text{3 kg} \cdot \dfrac{\text{1,000 g}}{\text{1 kg}}} \\ {} & = & {3 \cancel{\text{kg}} \cdot \dfrac{\text{1,000 g}}{1 \cancel{\text{kg}}}} \\ {} & = & {3 \cdot 1,000 \text{ g}} \\ {} & = & {3,000 \text{ g}} \end{array}\)

    Conjunto de Muestras A

    Convierte 67.2 hectolitros en mililitros.

    Solución

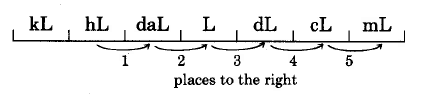
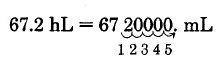
    Una línea con marcas hash dividiendo la línea en siete segmentos. Los segmentos están etiquetados, de izquierda a derecha, kL, hL, dal, L, dL, cL y mL. Debajo de hL, dal, L, dL, cL y mL son flechas que apuntan desde cada segmento al segmento vecino a la derecha. Estas flechas están etiquetadas del 1 al 5 indicando el número de lugares a la derecha.62.7 hL es igual a 6720000 mL. Se dibuja una flecha debajo de los cinco dígitos más a la derecha en 6720000, contando cinco decimales a la derecha.

    Así,\(\text{67.2 hL = 6,720,000 mL}\).

    Conjunto de Muestras A

    Convierte 100.07 centímetros a metros.

    Solución

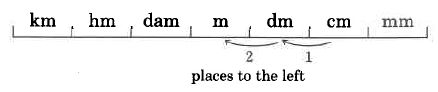
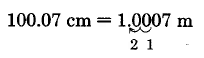
    Una línea con marcas hash dividiendo la línea en siete segmentos. Los segmentos están etiquetados, de izquierda a derecha, km, hm, presa, m, dm, cm, mm. Por debajo de cm, dm y m hay flechas que apuntan desde cada segmento al segmento vecino de la izquierda. Estas flechas están etiquetadas con 1 y 2, indicando el número de lugares a la izquierda.100.07 cm equivale a 1.0007 m. Las flechas debajo de los dos ceros más a la izquierda están etiquetadas con 1 y 2, apuntando a la izquierda, indicando el número de decimales movidos.

    Así,\(\text{100.07 cm = 1.0007m}\).

    Conjunto de Muestras A

    Convierta 0.16 miligramos en gramos.

    Solución

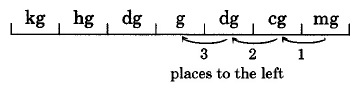
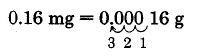
    Una línea con marcas hash dividiendo la línea en siete segmentos. Los segmentos están etiquetados, de izquierda a derecha, kg, hg, dg, g, dg, cg y mg. Debajo de g, dg, cg y mg hay flechas que apuntan desde cada segmento al segmento vecino de la izquierda. Estas flechas están etiquetadas con 1, 2 y 3, indicando el número de lugares a la izquierda.0.16mg equivale a 0.00016g. Debajo de los tres ceros más a la derecha hay flechas que apuntan a la izquierda, etiquetadas con 1, 2 y 3, indicando el movimiento del punto decimal.

    Así,\(\text{0.16 mg = 0.00016}\).

    Conjunto de práctica A

    Convierte 411 kilogramos en gramos.

    Contestar

    411,000 g

    Conjunto de práctica A

    Convierte 5.626 litros en centilitros.

    Contestar

    562.6 cL

    Conjunto de práctica A

    Convierte 80 mililitros en kilolitros.

    Contestar

    0.00008 kL

    Conjunto de práctica A

    Convierte 150 miligramos en centigramos.

    Contestar

    15 cg

    Conjunto de práctica A

    Convierte 2.5 centímetros a metros.

    Contestar

    0.025 m

    Ejercicios

    Hacer cada conversión.

    Ejercicio\(\PageIndex{1}\)

    87 m a cm

    Contestar

    8,700 cm

    Ejercicio\(\PageIndex{2}\)

    905 L a mL

    Ejercicio\(\PageIndex{3}\)

    16,005 mg a g

    Contestar

    16.005 g

    Ejercicio\(\PageIndex{4}\)

    48.66 L a dL

    Ejercicio\(\PageIndex{5}\)

    11.161 kL a L

    Contestar

    11,161 L

    Ejercicio\(\PageIndex{6}\)

    521.85 cm a mm

    Ejercicio\(\PageIndex{7}\)

    1.26 dag a dg

    Contestar

    126 dg

    Ejercicio\(\PageIndex{8}\)

    Presa 99.04 a cm

    Ejercicio\(\PageIndex{9}\)

    0.51 kL a dAL

    Contestar

    5.1 dAL

    Ejercicio\(\PageIndex{10}\)

    0.17 kL a dAL

    Ejercicio\(\PageIndex{11}\)

    0.05 m a dm

    Contestar

    0.5 dm

    Ejercicio\(\PageIndex{12}\)

    0.001 km a mm

    Ejercicio\(\PageIndex{13}\)

    8.106 hg a cg

    Contestar

    81,060 cg

    Ejercicio\(\PageIndex{14}\)

    17.0186 kL a mL

    Ejercicio\(\PageIndex{15}\)

    3 cm a m

    Contestar

    0.03 m

    Ejercicio\(\PageIndex{16}\)

    9 mm a m

    Ejercicio\(\PageIndex{17}\)

    4 g a mg

    Contestar

    4,000 mg

    Ejercicio\(\PageIndex{18}\)

    2 L a kL

    Ejercicio\(\PageIndex{19}\)

    6 kg a mg

    Contestar

    6,000,000 mg

    Ejercicio\(\PageIndex{20}\)

    7 dAL a mL

    Ejercicios para la revisión

    Ejercicio\(\PageIndex{21}\)

    Encuentra el valor de\(\dfrac{5}{8} - \dfrac{1}{3} + \dfrac{3}{4}\)

    Contestar

    \(\dfrac{25}{24} = 1 \dfrac{1}{24}\)

    Ejercicio\(\PageIndex{22}\)

    Resolver la proporción:\(\dfrac{9}{x} = \dfrac{27}{60}\).

    Ejercicio\(\PageIndex{23}\)

    Utilice el método de redondeo para estimar la suma:\(8,226 + 4,118\).

    Contestar

    12,300 (12,344)

    Ejercicio\(\PageIndex{24}\)

    Utilice el método de agrupamiento para estimar la suma:\(87 + 121 + 118 + 91 + 92\).

    Ejercicio\(\PageIndex{25}\)

    Convertir 3 in. a yd.

    Contestar

    \(0.08\overline{3}\)patio.

    This page titled 9.2: El Sistema Métrico de Medición is shared under a CC BY license and was authored, remixed, and/or curated by Denny Burzynski & Wade Ellis, Jr. (OpenStax CNX) .