9.3: Simplificación de Números Denominados

Última actualización
Guardar como PDF

Page ID: 116245

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de convertir una unidad de medida no simplificada en una unidad de medida simplificada
ser capaz de sumar y restar denominar números
ser capaz de multiplicar y dividir un número denominado por un número entero

Convertir a varias unidades

Definición: Denominar números

Los números que tienen unidades de medida asociadas a ellos se denominan números denominados. A menudo es conveniente, o incluso necesario, simplificar un número denominado.

Definición: Números de Denominación Simplificada

Un número denominado se simplifica cuando el número de unidades de medida estándar asociadas con él no supera el siguiente tipo de unidad superior.

El número denominado 55 min se simplifica ya que es menor que el siguiente tipo de unidad superior, 1 hr. El número denominado 65 min no se simplifica ya que no es menor que el siguiente tipo de unidad superior, 1 hr. El número denominado 65 min se puede simplificar a 1 hr 5 min. El número denominado 1 hr 5 min se simplifica ya que el siguiente tipo de unidad superior es el día, y 1 hr no supera 1 día.

Conjunto de Muestras A

Simplificar 19 pulg.

Solución

Ya que$\text{12 in. = 1 ft.}$, y$19 = 12 + 7$.

$\begin{array} {rcl} {\text{19 in.}} & = & {\text{12 in. + 7 in.}} \\ {} & = & {\text{1 ft + 7 in.}} \\ {} & = & {\text{1 ft 7 in.}} \end{array}$

Conjunto de Muestras A

Simplifica 4 gal 5 qt.

Solución

Ya que$\text{4 qt = 1 gal}$, y$5 = 4 + 1$.

$\begin{array} {rcl} {\text{4 gal 5 qt}} & = & {\text{4 gal + 4 qt + 1 qt}} \\ {} & = & {\text{4 gal + 1 gal + 1 qt}} \\ {} & = & {\text{5 gal + 1 qt}} \\ {} & = & {\text{5 gal 1 qt}}\end{array}$

Conjunto de Muestras A

Simplifica 2 hr 75 min.

Solución

Ya que$\text{60 min = 1 hr}$, y$75 = 60 + 15$.

$\begin{array} {rcl} {\text{2 hr 75 min}} & = & {\text{2 hr + 60 min + 15 min}} \\ {} & = & {\text{2 hr + 1 hr + 15 min}} \\ {} & = & {\text{3 hr + 15 min}} \\ {} & = & {\text{3 hr 15 min}}\end{array}$

Conjunto de Muestras A

Simplifica 43 fl oz.

Solución

Desde$\text{8 fl oz = 1 c}$ (1 taza), y$43 \div 8 = \text{5R3}$.

$\begin{array} {rcl} {\text{43 fl oz}} & = & {\text{40 fl oz + 3 fl oz}} \\ {} & = & {5 \cdot 8 \text{ fl oz + 3 fl oz}} \\ {} & = & {5 \cdot 1 \text{ c + 3 fl oz}} \\ {} & = & {\text{5 c + 3 fl oz}}\end{array}$

Pero,$\text{2c = 1 pt}$ y$5 \div 2 = \text{2R1}$. Entonces,

$\begin{array} {rcl} {\text{5 c + 3 fl oz}} & = & {2 \cdot 2 \text{ c + 1 c + 3 fl oz}} \\ {} & = & {2 \cdot 1 \text{ pt + 1 c + 3 fl oz}} \\ {} & = & {\text{2 pt + 1 c + 3 fl oz}} \end{array}$

Pero,$\text{2 pt = 1 qt}$, entonces

$\text{2 pt + 1 c + 3 fl oz = 1 qt 1 c 3 fl oz}$

Conjunto de práctica A

Simplificar cada número denominado. Consulte las tablas de conversión dadas en [link], si es necesario.

18 in.

Contestar: 1 pie 6 in.

Conjunto de práctica A

8 galones 9 qt

Contestar: 10 gal 1 qt

Conjunto de práctica A

5 hr 80 min

Contestar: 6 hr 20 min

Conjunto de práctica A

8 semanas 11 da

Contestar: 9 semanas 4 da

Conjunto de práctica A

86 da

Contestar: 12 semanas 2 da

Sumar y restar números denominados

Sumar y restar números denominados Los números
denominados se pueden sumar o restar mediante:

escribir los números verticalmente para que las unidades similares aparezcan en la misma columna.
sumando o restando el número de partes, llevando a lo largo de la unidad.
simplificando la suma o diferencia.

Conjunto de Muestras B

Agregue 6 pies 8 pulg. a 2 pies 9 pulg.

Solución

$\begin{array} {r} {\text{6 ft 8 in.}} \\ {\underline{\text{+ 2 ft 9 in.}}} \\ {\text{8 ft 17 in.}} \end{array}$Simplificar este número denominado.

Desde$\text{12 in. = 1 ft.}$

$\begin{array} {rcl} {\text{8 ft + 12 in. + 5 in.}} & = & {\text{8 ft + 1 ft + 5 in.}} \\ {} & = & {\text{9 ft + 5 in.}} \\ {} & = & {\text{9 ft 5 in.}} \end{array}$

Conjunto de Muestras B

Restar 5 da 3 hr de 8 da 11 hr.

Solución

$\begin{array} {r} {\text{8 da 11 hr}} \\ {\underline{\text{- 5 da 3 hr}}} \\ {\text{3 da 8 hr}} \end{array}$

Conjunto de Muestras B

Restar 3 lb 14 oz de 5 lb 3 oz.

Solución

$\begin{array} {r} {\text{5 lb 3 oz}} \\ {\underline{\text{- 3 lb 14 oz}}} \end{array}$

No podemos restar directamente 14 oz de 3 oz, por lo que debemos tomar prestadas 16 oz de las libras.

$\begin{array} {rcl} {\text{5 lb 3 oz}} & = & {\text{5 lb + 3 oz}} \\ {} & = & {\text{4 lb + 1 lb + 3 oz}} \\ {} & = & {\text{4 lb + 16 oz + 3 oz (Since 1 lb = 16 oz.)}} \\ {} & = & {\text{4 lb + 19 oz}} \\ {} & = & {\text{4 lb 19 oz}} \end{array}$

$\begin{array} {r} {\text{4 lb 19 oz}} \\ {\underline{\text{- 3 lb 14 oz}}} \\ {\text{1 lb 5 oz}} \end{array}$

Conjunto de Muestras B

Restar 4 da 9 hr 21 min de 7 da 10 min.

Solución

$\begin{array} {r} {\text{7 da 0 hr 10 min}} \\ {\underline{\text{- 4 da 9 hr 21 min}}} \end{array}$Toma prestada 1 da de la 7 da.

$\begin{array} {r} {\text{6 da 24 hr 10 min}} \\ {\underline{\text{- 4 da 9 hr 21 min}}} \end{array}$Pida prestada 1 hr a partir de las 24 hr.

$\begin{array} {r} {\text{6 da 23 hr 70 min}} \\ {\underline{\text{- 4 da 9 hr 21 min}}} \\ {\text{2 da 14 hr 49 min}} \end{array}$

Set de práctica B

Realizar cada operación. Simplifique cuando sea posible.

Agrega 4 gal 3 qt a 1 gal 2 qt.

Contestar: 6 galones 1 qt

Set de práctica B

Agregar 9 hr 48 min a 4 hr 26 min.

Contestar: 14 hr 14 min

Set de práctica B

Restar 2 pies 5 pulg. de 8 pies 7 pulg.

Contestar: 6 pies 2 in.

Set de práctica B

Restar 15 km 460 m de 27 km 800 m.

Contestar: 12 km 340 m

Set de práctica B

Restar 8 min 35 seg de 12 min 10 seg.

Contestar: 3 min 35 seg

Set de práctica B

Agrega 4 yd 2 ft 7 pulg. a 9 yd 2 ft 8 in.

Contestar: 14 yd 2 pies 3 pulg

Set de práctica B

Restar 11 min 55 seg de 25 min 8 seg.

Contestar: 13 min 13 seg

Multiplicar un Número Denominado por un Número Entero

Examinemos la suma repetida

$\underbrace{\text{4 ft 9 in. + 4 ft 9 in. + 4 ft 9 in.}}_{\text{3 times}} = \text{12 ft 27 in.}$

Recordando que la multiplicación es una descripción de suma repetida, por la propiedad distributiva que tenemos

$\begin{array} {rcl} {\text{3(4 ft 9 in.)}} & = & {\text{3 (4ft + 9 in.)}} \\ {} & = & {3 \cdot 4 \text{ ft } + 3 \cdot 9 \text{ in.}} \\ {} & = & {\text{12 ft + 27 in. Now, 27 in. = 2 ft 3 in.}} \\ {} & = & {\text{12 ft + 2 ft + 3 in.}} \\ {} & = & {\text{14 ft + 3 in.}} \\ {} & = & {\text{14 ft 3 in.}} \end{array}$

A partir de estas observaciones, podemos sugerir la siguiente regla.

Multiplicar un Número Denominado por un Número Entero
Para multiplicar un número denominado por un número entero, multiplique la parte numérica de cada unidad por el número entero y afije la unidad a este producto.

Conjunto de Muestras C

Realiza las siguientes multiplicaciones. Simplificar si es necesario.

$\begin{array} {rcl} {6 \cdot \text{(2 ft 4 in.)}} & = & {6 \cdot 2 \text{ ft + 6} \cdot 4 \text{in.}} \\ {} & = & {\text{12 ft + 24 in.}} \end{array}$

Desde$\text{3 ft = 1 yd}$ y$\text{12 in. = 1 ft.}$

$\begin{array} {rcl} {\text{12 ft + 24 in.}} & = & {\text{4 yd + 2 ft}} \\ {} & = & {\text{4 yd 2 ft}} \end{array}$

Conjunto de Muestras C

$\begin{array} {rcl} {8 \cdot \text{(5 hr 21 min 55 sec)}} & = & {8 \cdot 5 \text{ hr} + 8 \cdot 21 \text{ min} + 8 \cdot 55 \text{ sec}} \\ {} & = & {\text{40 hr + 168 min + 440 sec}} \\ {} & = & {\text{40 hr + 168 min + 7 min + 20 sec}} \\ {} & = & {\text{40 hr + 175 min + 20 sec}} \\ {} & = & {\text{40 hr + 2 hr + 55 min + 20 sec}} \\ {} & = & {\text{42 hr + 55 min + 20 sec}} \\ {} & = & {\text{24 hr + 18 hr + 55 min + 20 sec}} \\ {} & = & {\text{1 da + 18 hr + 55 min + 20 sec}} \\ {} & = & {\text{1 da 18 hr 55 min 20 sec}} \end{array}$

Set de práctica C

Realiza las siguientes multiplicaciones. Simplificar.

$2 \cdot \text{(10 min)}$

Contestar: 20 min

Set de práctica C

$5 \cdot \text{(3 qt)}$

Contestar: $\text{15 qt = 3 gal 3 qt}$

Set de práctica C

$4 \cdot \text{(5 ft 8 in.)}$

Contestar: $\text{20 ft 32 in. = 7 yd 1 ft 8 in.}$

Set de práctica C

$10 \cdot \text{(2 hr 15 min 40 sec)}$

Contestar: $\text{20 hr 150 min 400 sec = 22 hr 36 min 40 sec}$

Dividir un Número Denominado por un Número Entero

Dividir un Número Denominado por un Número Entero
Para dividir un número denominado por un número entero, divida la parte numérica de cada unidad por el número entero comenzando por la unidad más grande. Fijar la unidad a este cociente. Llevar cualquier resto a la siguiente unidad.

Conjunto de Muestras D

Realizar las siguientes divisiones. Simplificar si es necesario.

$\text{(12 min 40 sec)} \div 4$

Solución

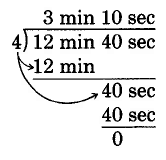
$División larga. 12 min y 40 seg divididos por 4. 4 pasa a 12 minutos 3 veces, haciendo un cociente de 3 minutos sin resto. 4 va a 40 segundos 10 veces, haciendo un cociente de 10 segundos sin resto. El cociente total es de 3 min 10 seg.$

Así$\text{(12 min 40 sec)} \div 4 = \text{3 min 10 sec}$

Conjunto de Muestras D

$\text{(5 yd 2 ft 9 in.)} \div 3$

Solución

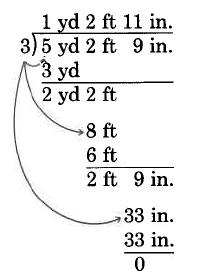
$División larga. 5 yd 2 ft 9 in dividido por 3. 3 va a 5 yardas una vez con un resto de 2 yardas. Baje los 2 pies. 2 yardas y 2 pies son ocho pies. 3 entra en ocho pies dos veces con un resto de 2 pies. Baje las 9 pulgadas. 2 pies 9 pulgadas es igual a 22 pulgadas. 3 entra en 33 pulgadas exactamente 11 veces. El cociente total es de 1 yd 2 pies 11 in.$

$\begin{array} {c} {\text{Convert to feet: 2 yd 2 ft = 8 ft}} \\ {\text{Convert to inches: 2 ft 9 in. = 33 in.}} \end{array}$

Así$\text{(5 yd 2 ft 9 in.)} \div 3 = \text{1 yd 2 ft 11 in.}$

Set de Práctica D

Realizar las siguientes divisiones. Simplificar si es necesario.

$\text{(18 hr 36 min)} \div 9$

Contestar: 2 hr 4 min

Set de Práctica D

$\text{(36 hr 8 min)} \div 8$

Contestar: 4 hr 18 min

Set de Práctica D

$\text{(13 yd 7 in.)} \div 5$

Contestar: 2 yd 1 ft 11 pulg

Set de Práctica D

$\text{(47 gal 2 qt 1 pt)} \div 3$

Contestar: 15 galones 3 qt 1 pt

Ejercicios

Para los siguientes 15 problemas, simplifique los números denominados.

Ejercicio$\PageIndex{1}$

16 in.

Contestar: 1 pie 4 pulgadas

Ejercicio$\PageIndex{2}$

19 pies

Ejercicio$\PageIndex{3}$

85 min

Contestar: 1 hora 25 minutos

Ejercicio$\PageIndex{4}$

90 min

Ejercicio$\PageIndex{5}$

17 da

Contestar: 2 semanas 3 días

Ejercicio$\PageIndex{6}$

25 oz

Ejercicio$\PageIndex{7}$

240 oz

Contestar: 15 libras

Ejercicio$\PageIndex{8}$

3,500 lb

Ejercicio$\PageIndex{9}$

26 qt

Contestar: 6 galones 2 cuartos

Ejercicio$\PageIndex{10}$

300 seg

Ejercicio$\PageIndex{11}$

135 oz

Contestar: 8 libras 7 onzas

Ejercicio$\PageIndex{12}$

14 cdta

Ejercicio$\PageIndex{13}$

18 pt

Contestar: 2 galones 1 cuarto

Ejercicio$\PageIndex{14}$

3,500 m

Ejercicio$\PageIndex{15}$

16,300 mL

Contestar: 16 litros 300 mililitros (o 1Dal 6 L 3dL)

Para los siguientes 15 problemas, realice las operaciones indicadas y simplifique las respuestas si es posible.

Ejercicio$\PageIndex{16}$

Agregar 6 min 12 seg a 5 min 15 seg.

Ejercicio$\PageIndex{17}$

Agregar 14 da 6 hr a 1 da 5 hr.

Contestar: 15 días 11 horas

Ejercicio$\PageIndex{18}$

Agrega 9 gal 3 qt a 2 gal 3 qt.

Ejercicio$\PageIndex{19}$

Agrega 16 lb 10 oz a 42 lb 15 oz.

Contestar: 59 libras 9 onzas

Ejercicio$\PageIndex{20}$

Restar 3 gal 1 qt de 8 gal 3 qt.

Ejercicio$\PageIndex{21}$

Restar 3 pies 10 pulg. De 5 pies 8 pulg.

Contestar: 1 pie 10 pulgadas

Ejercicio$\PageIndex{22}$

Restar 5 lb 9 oz de 12 lb 5 oz.

Ejercicio$\PageIndex{23}$

Restar 10 hr 10 min de 11 hr 28 min.

Contestar: 1 hora 18 minutos

Ejercicio$\PageIndex{24}$

Agrega 3 fl oz 1 cucharada 2 cdta a 5 fl oz 1 cucharada 2 cdta.

Ejercicio$\PageIndex{25}$

Agregar 4 da 7 hr 12 min a 1 da 8 hr 53 min.

Contestar: 5 días 16 horas 5 minutos

Ejercicio$\PageIndex{26}$

Restar 5 hr 21 seg de 11 hr 2 min 14 seg.

Ejercicio$\PageIndex{27}$

Restar 6 T 1,300 lb 10 oz de 8 T 400 lb 10 oz.

Contestar: 1 tonelada 1,100 libras (o 1T 1,100 lb)

Ejercicio$\PageIndex{28}$

Restar 15 mi 10 in. de 27 mi 800 ft 7 in.

Ejercicio$\PageIndex{29}$

Restar 3 semanas 5 da 50 min 12 seg de 5 semanas 6 da 20 min 5 seg.

Contestar: 2 semanas 23 horas 29 minutos 53 segundos

Ejercicio$\PageIndex{30}$

Restar 3 gal 3 qt 1 pt 1 oz de 10 gal 2 qt 2 oz.

Ejercicios para la revisión

Ejercicio$\PageIndex{31}$

Encuentra el valor:$(\dfrac{5}{8})^2 + \dfrac{39}{64}$.

Contestar: 1

Ejercicio$\PageIndex{32}$

Encuentra la suma:$8 + 6 \dfrac{3}{5}$.

Ejercicio$\PageIndex{33}$

Convertir$2.05 \dfrac{1}{11}$ a una fracción.

Contestar: $2 \dfrac{14}{275}$

Ejercicio$\PageIndex{34}$

Una solución ácida se compone de 3 partes de ácido por 7 partes de agua. ¿Cuántas partes de ácido hay en una solución que contiene 126 partes de agua?

Ejercicio$\PageIndex{35}$

Convierte 126 kg en gramos.

Contestar: 126,000 g