9.5: Área y Volumen de Figuras Geométricas y Objetos

Última actualización
Guardar como PDF

Page ID: 116246

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

conocer el significado y la notación para el área
conocer las fórmulas de área para algunas figuras geométricas comunes
ser capaz de encontrar las áreas de algunas figuras geométricas comunes
conocer el significado y la notación para el volumen
conocer las fórmulas de volumen para algunos objetos geométricos comunes
ser capaz de encontrar el volumen de algunos objetos geométricos comunes

Muy a menudo es necesario multiplicar un número denominado por otro. Para ello, multiplicamos las partes numéricas juntas y las partes unitarias juntas. Por ejemplo,

$\begin{array} {rcl} {\text{8 in.} \cdot \text{8 in.}} & = & {8 \cdot 8 \cdot \text{in.} \cdot \text{in.}} \\ {} & = & {64 \text{ in.}^2} \end{array}$

$\begin{array} {rcl} {\text{4 mm} \cdot \text{4 mm} \cdot \text{4 mm}} & = & {4 \cdot 4 \cdot 4 \cdot \text{mm} \cdot \text{mm} \cdot \text{mm}} \\ {} & = & {64 \text{ mm}^3} \end{array}$

En ocasiones el producto de unidades tiene un significado físico. En esta sección, examinaremos el significado de los productos$\text{(length unit)}^2$ y$\text{(length unit)}^3$

El significado y la notación para el área

El producto$\text{(length unit)} \cdot \text{(length unit)} = \text{(length unit)}^2$, o unidad de longitud cuadrada (unidad de longitud cuadrada), se puede interpretar físicamente como el área de una superficie.

Área
El área de una superficie es la cantidad de unidades de longitud cuadrada contenidas en la superficie.

Por ejemplo, 3 pulgadas cuadradas significa que 3 cuadrados, 1 pulgada en cada lado, se pueden colocar con precisión en alguna superficie. (Es posible que los cuadrados tengan que cortarse y reorganizarse para que coincidan con la forma de la superficie).

Examinaremos el área de las siguientes figuras geométricas.

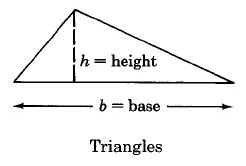
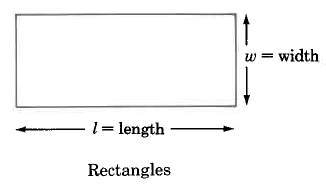
$Los triángulos, un polígono de tres lados, tienen una altura, h, medida de abajo hacia arriba, y base, b, medida de un extremo a otro del lado inferior.$ $Los rectángulos, un polígono de cuatro lados, tienen un ancho, w, en este caso el lado vertical, y un largo, l, en este caso el lado horizontal.$

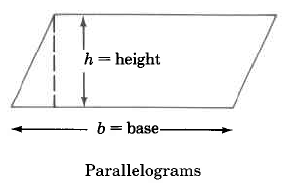
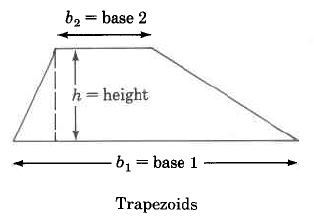
$Los paralelogramos, un polígono de cuatro lados con lados diagonales en la misma dirección tienen una altura, h, medida como la distancia de abajo hacia arriba, y una base, b, medida como el ancho del lado horizontal.$ $Los trapezoides, un polígono de cuatro lados con lados diagonales orientados apoyados entre sí, tienen una altura medida como la distancia entre las dos bases. Los trapezoides tienen dos bases de diferentes longitudes, la base 1 y la base 2.$

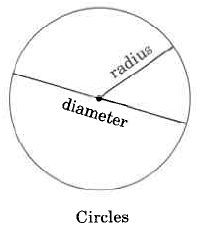
$Círculos. La distancia a través del círculo es el diámetro. La distancia desde el centro del círculo hasta el borde es el radio.$

Fórmulas de área

Podemos determinar las áreas de estas figuras geométricas utilizando las siguientes fórmulas.

	Figura	Fórmula de área	Declaración
$Un triángulo.$	Triángulo	$A_T = \dfrac{1}{2} \cdot b \cdot h$	El área de un triángulo es la mitad de la base por la altura.
$Un rectángulo.$	Rectángulo	$A_R = l \cdot w$	El área de un rectángulo es la longitud por el ancho.
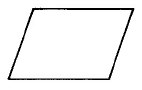$Un paralelogramo.$	Paralelogramo	$A_P = b \cdot h$	El área de un paralelogramo es la base por la altura.
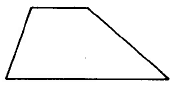$Un trapecio.$	Trapecio	$A_{Trap} = \dfrac{1}{2} \cdot (b_1 + b_2) \cdot h$	El área de un trapecio es la mitad de la suma de las dos bases por la altura.
$Un círculo.$	Círculo	$A_c = \pi r^2$	El área de un círculo es$\pi$ multiplicada por el cuadrado del radio.

Encontrar áreas de algunas figuras geométricas comunes

Conjunto de Muestras A

Encuentra el área del triángulo.

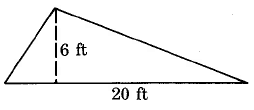
$Un triángulo con altura 6 pies y largo 20 pies.$

Solución

$\begin{array} {rcl} {A_T} & = & {\dfrac{1}{2} \cdot b \cdot h} \\ {} & = & {\dfrac{1}{2} \cdot 20 \cdot 5 \text{ sq ft}} \\ {} & = & {10 \cdot 6 \text{ sq ft}} \\ {} & = & {60 \text{ sq ft}} \\ {} & = & {60 \text{ ft}^2} \end{array}$

El área de este triángulo es de 60 pies cuadrados, que a menudo se escribe como 60$\text{ft}^2$.

Conjunto de Muestras A

Encuentra el área del rectángulo.

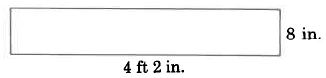
$Un rectángulo con ancho 4 pies 2 pulgadas y alto 8 pulgadas.$

Solución

Primero convertiremos 4 ft 2 in. a pulgadas. Como deseamos convertir a pulgadas, usaremos la fracción unitaria$\dfrac{\text{12 in.}}{\text{1 ft}}$ ya que tiene pulgadas en el numerador. Entonces,

$\begin{array} {rcl} {\text{4 ft}} & = & {\dfrac{\text{4 ft}}{1} \cdot \dfrac{\text{12 in.}}{\text{1 ft}}} \\ {} & = & {\dfrac{4 \cancel{\text{ ft}}}{1} \cdot \dfrac{\text{12 in.}}{1 \cancel{\text{ ft}}}} \\ {} & = & {\text{48 in.}} \end{array}$

Por lo tanto,$\text{4 ft 2 in. = 48 in. + 2 in. = 50 in.}$

$\begin{array} {rcl} {A_R} & = & {l \cdot w} \\ {} & = & {\text{50 in.} \cdot \text{8 in.}} \\ {} & = & {400 \text{ sq in.}} \end{array}$

El área de este rectángulo es de 400 pulgadas cuadradas.

Conjunto de Muestras A

Encuentra el área del paralelogramo.

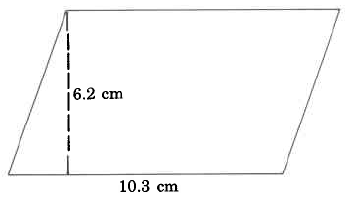
$Un paralelogramo con base 10.3cm y altura 6.2cm$

Solución

$\begin{array} {rcl} {A_P} & = & {b \cdot h} \\ {} & = & {\text{10.3 cm} \cdot \text{6.2 cm}} \\ {} & = & {63.86 \text{ sq cm}} \end{array}$

El área de este paralelogramo es de 63.86 cm cuadrados.

Conjunto de Muestras A

Encuentra el área del trapecio.

$Un trapecio con altura 4.1mm, base inferior 20.4mm, y base superior 14.5mm.$

Solución

$\begin{array} {rcl} {A_{Trap}} & = & {\dfrac{1}{2} \cdot (b_1 + b_2) \cdot h} \\ {} & = & {\dfrac{1}{2} \cdot (\text{14.5 mm + 20.4 mm}) \cdot (4.1 \text{ mm})} \\ {} & = & {\dfrac{1}{2} \cdot (\text{34.9 mm}) \cdot (4.1 \text{ mm})} \\ {} & = & {\dfrac{1}{2} \cdot \text{(143.09 sq mm)}} \\ {} & = & {71.545 \text{ sq mm}} \end{array}$

El área de este trapecio es de 71.545 mm cuadrados.

Conjunto de Muestras A

Encuentra el área aproximada del círculo.

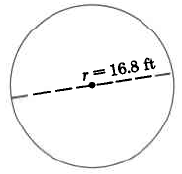
$Un círculo con radio 16.8ft.$

Solución

$\begin{array} {rcl} {A_c} & = & {\pi \cdot r^2} \\ {} & \approx & {(3.14) \cdot (16.8 \text{ ft})^2} \\ {} & \approx & {(3.14) \cdot (\text{282.24 sq ft})} \\ {} & \approx & {888.23 \text{ sq ft}} \end{array}$

El área de este círculo es de aproximadamente 886.23 pies cuadrados.

Conjunto de práctica A

Encuentra el área de cada una de las siguientes figuras geométricas.

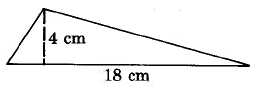
$Un triángulo con base 18cm y altura 4cm.$

Contestar: 36 cm cuadrados

Conjunto de práctica A

$Un rectángulo con base 9.26mm y altura 4.05mm.$

Contestar: 37.503 mm cuadrados

Conjunto de práctica A

$Un paralelogramo con base 5.1in y altura 2.6in.$

Contestar: 13.26 pulgadas cuadradas

Conjunto de práctica A

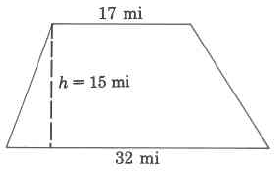
$Un trapecio con altura 15mi, base inferior 32mi, y base superior 17mi.$

Contestar: 367.5 sq mi

Conjunto de práctica A

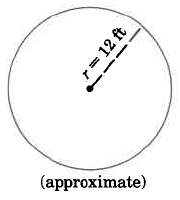
$Un círculo con radio r = 12ft.$

Contestar: 452.16 pies cuadrados

Conjunto de práctica A

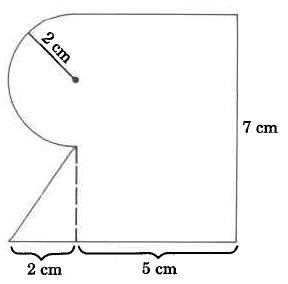
$Una forma compuesta por un medio círculo de radio 2cm, un rectángulo con base 5cm y altura 7cm, y un triángulo con base 2cm y altura 3cm.$

Contestar: 44.28 cm cuadrados

El significado y la notación para el volumen

El producto$\text{(length unit)}\text{(length unit)}\text{(length unit)} = \text{(length unit)}^3$, o unidad de longitud cúbica (unidad de longitud cúbica), se puede interpretar físicamente como el volumen de un objeto tridimensional.

Volumen
El volumen de un objeto es la cantidad de unidades de longitud cúbica contenidas en el objeto.

Por ejemplo, 4 cu mm significa que 4 cubos, de 1 mm en cada lado, llenarían con precisión algún objeto tridimensional. (Es posible que los cubos tengan que cortarse y reorganizarse para que coincidan con la forma del objeto).

$Un sólido rectangular, con largo l, ancho w y alto h.$ $Una esfera con radio r.$ $Un cilindro con altura h y radio r.$ $Un cono con altura h y radio r.$

Fórmulas de Volumen

	Figura	Fórmula de volumen	Declaración
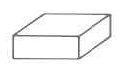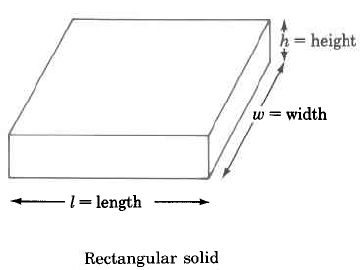
$Un sólido rectangular.$	Sólido rectangular	$\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	El volumen de un sólido rectangular es la longitud por la anchura por la altura.
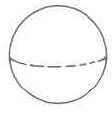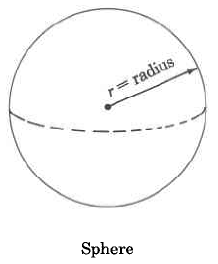
$Una esfera.$	Esfera	$V_s = \dfrac{4}{3} \cdot \pi \cdot r^3$	El volumen de una esfera es$\dfrac{4}{3}$$\pi$ multiplicado por el cubo del radio.
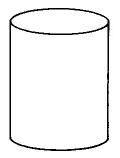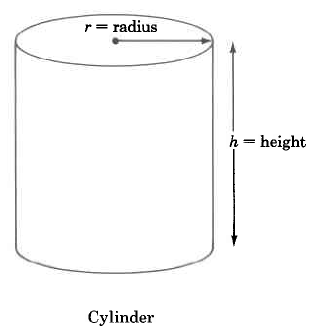
$Un cilindro.$	Cilindro	$\begin{array} {rcl} {V_{Cyl}} & = & {\pi \cdot r^2 \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	El volumen de un cilindro es$\pi$ multiplicado por el cuadrado del radio por la altura.
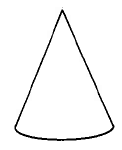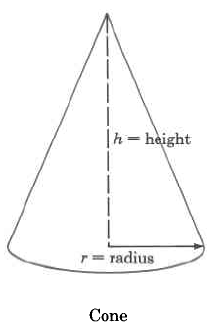
$Un cono.$	Cono	$\begin{array} {rcl} {V_c} & = & {\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	El volumen de un cono es$\dfrac{1}{3}$$\pi$ multiplicado por el cuadrado del radio por la altura.

Búsqueda de volúmenes de algunos objetos geométricos comunes

Conjunto de Muestras B

Encuentra el volumen del sólido rectangular.

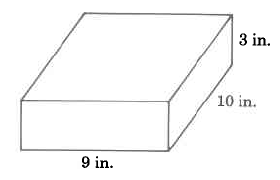
$Un sólido rectangular con ancho 9in, largo 10in y alto 3".$

Solución

$\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{9 in.} \cdot \text{10 in.} \cdot \text{3 in.}} \\ {} & = & {\text{270 cu in.}} \\ {} & = & {\text{270 in.}^3} \end{array}$

El volumen de este sólido rectangular es de 270 pulgadas cúbicas.

Conjunto de Muestras B

Encuentra el volumen aproximado de la esfera.

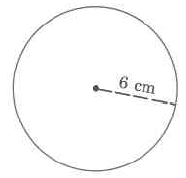
$Un círculo con radio de 6cm.$

Solución

$\begin{array} {rcl} {V_S} & = & {\dfrac{4}{3} \cdot \pi \cdot r^3} \\ {} & \approx & {(\dfrac{4}{3}) \cdot (3.14) \cdot \text{(6 cm)}^3} \\ {} & \approx & {(\dfrac{4}{3}) \cdot (3.14) \cdot \text{(216 cu cm)}} \\ {} & \approx & {\text{904.32 cu cm}} \end{array}$

El volumen aproximado de esta esfera es de 904.32 cu cm, que a menudo se escribe como 904.32$^3$ cm.

Conjunto de Muestras B

Encuentra el volumen aproximado del cilindro.

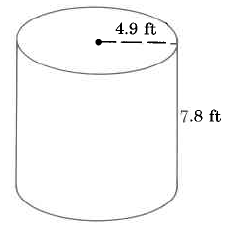
$Un cilindro con radio 4.9ft y altura 7.8ft.$

Solución

$\begin{array} {rcl} {V_{Cyl}} & = & {\pi \cdot r^2 \cdot h} \\ {} & \approx & {(3.14) \cdot (\text{4.9 ft})^2 \cdot \text{(7.8 ft)}} \\ {} & \approx & {(3.14) \cdot (\text{24.01 sq ft}) \cdot \text{(7.8 ft)}} \\ {} & \approx & {(3.14) \cdot \text{(187.278 cu ft)}} \\ {} & \approx & {\text{588.05292 cu ft}} \end{array}$

El volumen de este cilindro es aproximadamente 588.05292 pies cúbicos. El volumen es aproximado porque nos aproximamos$\pi$ con 3.14.

Conjunto de Muestras B

Encuentra el volumen aproximado del cono. Redondear a dos decimales.

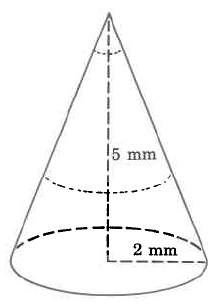
$Un cono con altura 5mm y radio 2mm$

Solución

$\begin{array} {rcl} {V_{c}} & = & {\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{2 mm})^2 \cdot \text{(5 mm)}} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{4 sq mm}) \cdot \text{(5 mm)}} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot \text{(20 cu mm)}} \\ {} & \approx & {20.9\overline{3} \text{ cu mm}} \\ {} & \approx & {\text{20.93 cu mm}} \end{array}$

El volumen de este cono es de aproximadamente 20.93 cu mm. El volumen es aproximado porque nos aproximamos$\pi$ con 3.14.

Set de práctica B

Encuentra el volumen de cada objeto geométrico. Si$\pi$ se requiere, aproximarlo con 3.14 y encontrar el volumen aproximado.

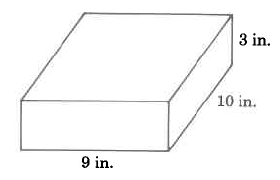
$Un sólido rectangular con ancho 9in, largo 10in y alto 3".$

Contestar: 21 cu pulg.

Set de práctica B

Esfera

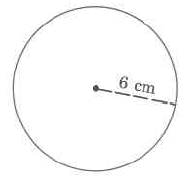
$Una esfera con radio de 6cm.$

Contestar: 904.32 pies cúbicos

Set de práctica B

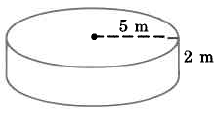
$Un cilindro con radio 5m y altura 2m.$

Contestar: 157 cu m

Set de práctica B

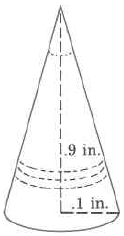
$Un cono con altura de .9in y radio de .1 pulg.$

Contestar: 0.00942 pulgadas cúbicas.

Ejercicios

Encuentra cada medición indicada.

Ejercicio$\PageIndex{1}$

Área

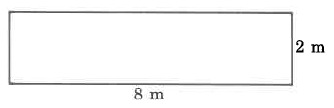
$Un rectángulo con ancho 8m y alto 2m$

Contestar: 16 metros cuadrados

Ejercicio$\PageIndex{2}$

Área

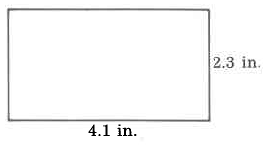
$Un rectángulo con ancho 4.1in y alto 2.3in.$

Ejercicio$\PageIndex{3}$

Área

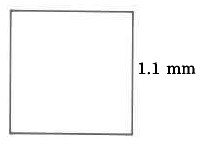
Contestar: 1.21 mm cuadrados

Ejercicio$\PageIndex{4}$

Área

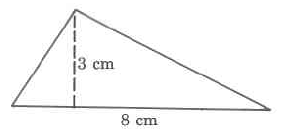
$Un triángulo con base 8cm y altura 3cm.$

Ejercicio$\PageIndex{5}$

Área

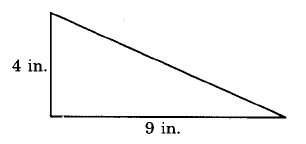
$Un triángulo con base 9in y altura 4in.$

Contestar: 18 pulg.

Ejercicio$\PageIndex{6}$

Área

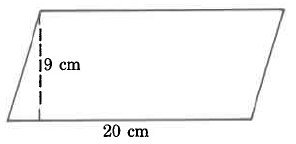
$Un paralelogramo con base 20cm y altura 9cm.$

Ejercicio$\PageIndex{7}$

Área exacta

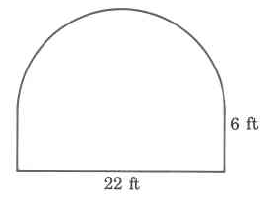
$Un rectángulo con un semicírculo en la parte superior. El ancho del rectángulo es de 22 pies, que también es el diámetro del círculo, y la altura del rectángulo es de 6 pies.$

Contestar: $(60.5 \pi + 132) \text{ sq ft}$

Ejercicio$\PageIndex{8}$

Área aproximada

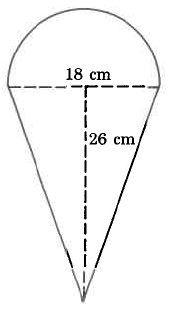
$Un triángulo con un semicírculo en la parte superior, como un cono de helado. El diámetro del círculo es de 18 cm y la altura del triángulo es de 26 cm.$

Ejercicio$\PageIndex{9}$

Área

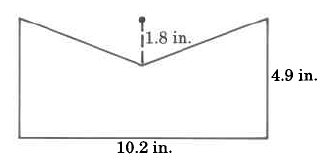
Contestar: 40.8 pulg.

Ejercicio$\PageIndex{10}$

Área

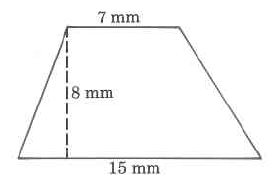
$Un trapecio con base inferior de 15 mm, base superior de 7 mm y altura de 8 mm.$

Ejercicio$\PageIndex{11}$

Área aproximada

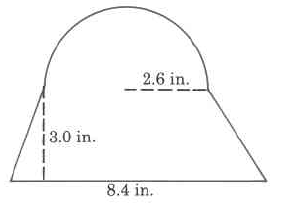
$Una forma compuesta por un trapecio con un semicírculo en la parte superior. El diámetro del círculo es el ancho de la base superior. La base inferior es 8.4in, la altura de la porción trapezoidal es 3.0in, y el radio del círculo es 2.6in.$

Contestar: 31.0132 pulgadas cuadradas

Ejercicio$\PageIndex{12}$

Área exacta

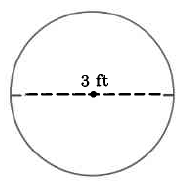
$Un círculo con un diámetro de 3 pies.$

Ejercicio$\PageIndex{13}$

Área aproximada

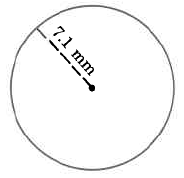
$Un círculo con un radio de 7.1mm.$

Contestar: 158.2874 mm cuadrados

Ejercicio$\PageIndex{14}$

Área exacta

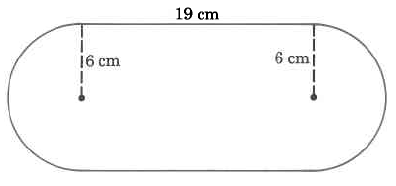
$Una forma que parece una pista de hielo. Un rectángulo con un semicírculo unido a cada extremo. El radio de los semicírculos es de 6cm y la longitud del rectángulo es de 19cm.$

Ejercicio$\PageIndex{15}$

Área aproximada

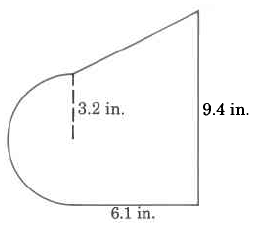
$Un trapecio con un semicírculo unido a una base. El radio del semicírculo es 3.2in. La otra base es 9.4in. La altura del trapecio es de 6.1in.$

Contestar: 64.2668 pulgadas cuadradas

Ejercicio$\PageIndex{16}$

Área

$Un rectángulo con un rectángulo recortado por dentro. El rectángulo interior tiene un ancho de 4.83in y una altura de 1.61in. El rectángulo exterior tiene un ancho de 5.21in y una altura de 1.74in.$

Ejercicio$\PageIndex{17}$

Área aproximada

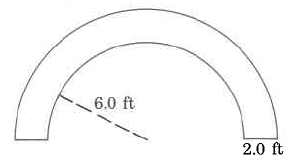
$Una forma de tubo en medio círculo. El radio del círculo interno es 6.0ft. El grosor del tubo es de 2.0 pies.$

Contestar: 43.96 pies cuadrados

Ejercicio$\PageIndex{18}$

Volumen

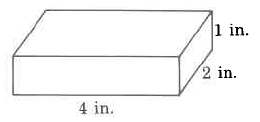
$Un sólido rectangular con ancho 4 pulgadas, largo 2 pulgadas y alto 1 pulgadas.$

Ejercicio$\PageIndex{19}$

Volumen

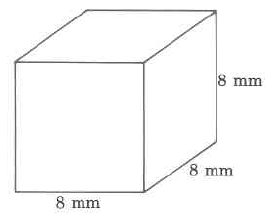
$Un sólido rectangular con 8 mm de ancho, 8 mm de largo y 8 mm de altura.$

Contestar: 512 cm cu

Ejercicio$\PageIndex{20}$

Volumen exacto

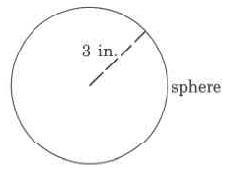
$Una esfera con un radio de 3 pulgadas.$

Ejercicio$\PageIndex{21}$

Volumen aproximado

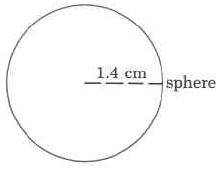
$Una esfera con un radio de 1.4cm.$

Contestar: 11.49 cu cm

Ejercicio$\PageIndex{22}$

Volumen aproximado

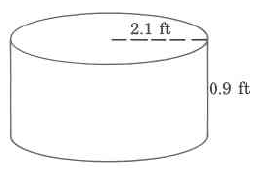
$Un cilindro con un radio de 2.1ft y una altura de 0.9ft.$

Ejercicio$\PageIndex{23}$

Volumen exacto

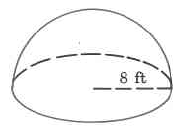
$La mitad de una esfera con radio de 8 pies.$

Contestar: $\dfrac{1024}{3} \pi \text{ cu ft}$

Ejercicio$\PageIndex{24}$

Volumen aproximado

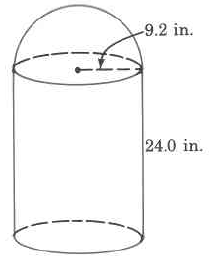
$Un cilindro con media esfera en la parte superior. El radio del objeto es 9.2in y la altura del cilindro es 24.0in.$

Ejercicio$\PageIndex{25}$

Volumen aproximado

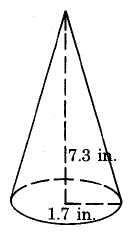
$Un cono con radio 1.7in y altura 7.3in.$

Contestar: 22.08 pulg.

Ejercicio$\PageIndex{26}$

Volumen aproximado

$Un cilindro con un cono en la parte superior. El objeto tiene un diámetro de 3.0ft. El cono tiene una altura de 3.0ft. La altura del cilindro es de 8.1ft.$

Ejercicios para la revisión

Ejercicio$\PageIndex{27}$

En el número 23,426, ¿cuántos cientos hay?

Contestar: 4

Ejercicio$\PageIndex{28}$

Listar todos los factores de 32.

Ejercicio$\PageIndex{29}$

Encuentra el valor de$4 \dfrac{3}{4} - 3 \dfrac{5}{6} + 1 \dfrac{2}{3}$.

Contestar: $\dfrac{31}{12} = 2 \dfrac{7}{12} = 2.58$

Ejercicio$\PageIndex{30}$

Encuentra el valor de$\dfrac{5 + \dfrac{1}{3}}{2 + \dfrac{2}{15}}$.

Ejercicio$\PageIndex{31}$

Encuentra el perímetro.

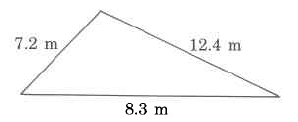
$Un triángulo con lados de las siguientes longitudes: 7.2m, 8.3m y 12.4m.$

Contestar: 27.9m