10.2: Números firmados

Última actualización
Guardar como PDF

Page ID: 116528

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de distinguir entre números reales positivos y negativos
ser capaz de leer números firmados
entender el origen y uso de la propiedad del producto de doble negativo

Números positivos y negativos

Definición: Números positivos y negativos

Cada número real que no sea cero tiene un signo asociado a él. Se dice que un número real es un número positivo si está a la derecha de 0 en la línea numérica y negativo si está a la izquierda de 0 en la línea numérica.

La notación de números firmados

+ y − Notación
Un número se denota como positivo si está precedido directamente por un signo más o ningún signo en absoluto.
Un número se denota como negativo si va precedido directamente por un signo menos.

Lectura de números firmados

Los signos más y menos ahora tienen dos significados:

El signo más puede denotar la operación de suma o un número positivo.

El signo menos puede denotar la operación de resta o un número negativo.

Para evitar cualquier confusión entre “signo” y “operación”, es preferible leer el signo de un número como “positivo” o “negativo”. Cuando se usa “+” como señal de operación, se lee como “más”. Cuando se usa “-” como signo de operación, se lee como “menos”.

Conjunto de Muestras A

Lee cada expresión para evitar confusiones entre “operación” y “señal”.

-8 debe leerse como “ocho negativo” en lugar de “menos ocho”.

Conjunto de Muestras A

$4 + (-2)$debe leerse como “cuatro más dos negativos” en lugar de “cuatro más menos dos”.

Conjunto de Muestras A

$-6 + (-3)$debe leerse como “seis negativos más tres negativos” en lugar de “menos seis más menos tres”.

Conjunto de Muestras A

$-15 - (-6)$debe leerse como “quince menos seis negativos” en lugar de “menos quince menos seis”.

Conjunto de Muestras A

$-5 + 7$debe leerse como “cinco negativos más siete” en lugar de “menos cinco más siete”.

Conjunto de Muestras A

$0 - 2$debe leerse como “cero menos dos”.

Conjunto de práctica A

Escribe cada expresión en palabras.

$6 + 1$

Contestar: seis más uno

Conjunto de práctica A

$2 + (-8)$

Contestar: dos más ocho negativo

Conjunto de práctica A

$-7 + 5$

Contestar: menos siete más cinco

Conjunto de práctica A

$-10 - (+3)$

Contestar: menos diez menos tres

Conjunto de práctica A

$-1 - (-8)$

Contestar: menos uno menos menos ocho

Conjunto de práctica A

$0 + (-11)$

Contestar: cero más once negativo

Opuestos

Opuestos
En la recta numérica, cada número real, distinto de cero, tiene una imagen en el lado opuesto de 0. Por ello, decimos que cada número real tiene un opuesto. Los opuestos están a la misma distancia de cero pero tienen signos opuestos.

Lo contrario de un número real se denota colocando un signo negativo directamente frente al número. Así, si$a$ hay algún número real, entonces$-a$ es su opuesto.

Nota

La letra "$a$" es una variable. Por lo tanto,$a$ "" no necesita ser positivo, y ""$-a$ "no tiene por qué ser negativo.

Si\ 9a\) es cualquier número real,$-a$ es opuesto$a$ en la línea numérica.

$Dos líneas de números. Una línea numérica con marcas hash de izquierda a derecha, -a, 0 y a. Esta línea numérica se titula como positiva. Una segunda línea numérica con marcas hash de izquierda a derecha, a, 0 y -a. Esta línea numérica se titula como negativo.$

La propiedad Doble Negativa

El número$a$ es opuesto$-a$ en la recta numérica. Por lo tanto,$-(-a)$ es opuesto$-a$ en la recta numérica. Esto significa que$-(-a) = a$

De esta propiedad de opuestos, podemos sugerir la propiedad doble negativa para números reales.

Propiedad Doble Negativa:$-(-a) = a$
Si$a$ es número real, entonces
$-(-a) = a$

Conjunto de Muestras B

Encuentra lo contrario de cada número.

Si$a = 2$, entonces$-a = -2$, También,$-(-a) = -(-2) = 2$.

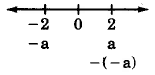
$Una línea numérica con marcas hash de izquierda a derecha, -2, 0 y 2. Por debajo del -2 es -a, y por debajo del 2 está a, o - (-a).$

Conjunto de Muestras B

Si$a = -4$, entonces$-a = -(-4) = 4$, También,$-(-a) = a = -4$.

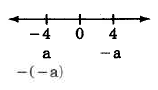
$Una línea numérica con marcas hash de izquierda a derecha, -4, 0 y 4. Por debajo del -4 es a, o - (-a), y por debajo del 2 es -a.$

Set de práctica B

Encuentra lo contrario de cada número.

Contestar: -8

Set de práctica B

Contestar: -17

Set de práctica B

-6

Contestar: 6

Set de práctica B

-15

Contestar: 15

Set de práctica B

- (-1)

Contestar: -1

Set de práctica B

− [− (−7)]

Contestar: 7

Set de práctica B

Supongamos que$a$ es un número positivo. ¿Es$-a$ positivo o negativo?

Contestar: $-a$es negativo

Set de práctica B

Supongamos que$a$ es un número negativo. ¿Es$-a$ positivo o negativo?

Contestar: $-a$es positivo

Set de práctica B

Supongamos que no conocemos el signo del número$k$. ¿Es$-k$ positivo, negativo, o no lo sabemos?

Contestar: -17

Debemos decir que no sabemos.

Ejercicios

Ejercicio$\PageIndex{1}$

Un número se denota como positivo si va precedido directamente por.

Contestar: + (o sin señal)

Ejercicio$\PageIndex{2}$

Un número se denota como negativo si va precedido directamente por.

¿Cómo se debe leer el número en los siguientes 6 problemas? (Escribe en palabras.)

Ejercicio$\PageIndex{3}$

-7

Contestar: siete menos

Ejercicio$\PageIndex{4}$

-5

Ejercicio$\PageIndex{5}$

Contestar: quince

Ejercicio$\PageIndex{6}$

Ejercicio$\PageIndex{7}$

- (-1)

Contestar: negativo negativo uno, u opuesto negativo uno

Ejercicio$\PageIndex{8}$

- (-5)

Para los siguientes 6 problemas, escriba cada expresión en palabras.

Ejercicio$\PageIndex{9}$

5 + 3

Contestar: cinco más tres

Ejercicio$\PageIndex{10}$

3 + 8

Ejercicio$\PageIndex{11}$

15 + (-3)

Contestar: quince más tres negativos

Ejercicio$\PageIndex{12}$

1 + (-9)

Ejercicio$\PageIndex{13}$

-7 - (-2)

Contestar: menos siete menos menos menos dos

Ejercicio$\PageIndex{14}$

0 - (-12)

Para los siguientes 6 problemas, reescriba cada número de forma más simple.

Ejercicio$\PageIndex{15}$

- (-2)

Contestar: 2

Ejercicio$\PageIndex{16}$

- (-16)

Ejercicio$\PageIndex{17}$

- [- (-8)]

Contestar: -8

Ejercicio$\PageIndex{18}$

- [- (-20)]

Ejercicio$\PageIndex{19}$

7 - (-3)

Contestar: 7 + 3 = 10

Ejercicio$\PageIndex{20}$

6 - (-4)

Ejercicios para la revisión

Ejercicio$\PageIndex{21}$

Encontrar el cociente;$8 \div 27$.

Contestar: $0.\overline{296}$

Ejercicio$\PageIndex{22}$

Resuelve la proporción:$\dfrac{5}{9} = \dfrac{60}{x}$

Ejercicio$\PageIndex{23}$

Utilice el método de redondeo para estimar la suma:$5829 + 8767$

Contestar: $6,000 + 9,000 = 15,000$$(5,829 + 8,767 = 14,596)$o$5,800 + 8,800 + 14,600$

Ejercicio$\PageIndex{24}$

Use una fracción unitaria para convertir 4 yd a pies.

Ejercicio$\PageIndex{25}$

Convierte 25 cm a hm.

Contestar: 0.0025 hm