10.1: Variables, constantes y números reales

Última actualización
Guardar como PDF

Page ID: 116527

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de distinguir entre variables y constantes
ser capaz de reconocer un número real y subconjuntos particulares de los números reales
entender el orden de los números reales

Variables y Constantes

Una distinción básica entre álgebra y aritmética es el uso de símbolos (generalmente letras) en álgebra para representar números. Entonces, el álgebra es una generalización de la aritmética. Veamos dos ejemplos de situaciones en las que las letras son sustituidas por números:

Supongamos que un estudiante está tomando cuatro clases universitarias, y cada clase puede tener como máximo 1 examen por semana. En cualquier periodo de 1 semana, el alumno podrá tener 0, 1, 2, 3 o 4 exámenes. En álgebra, podemos dejar que la letra$x$ represente el número de exámenes que este estudiante puede tener en un periodo de 1 semana. La letra$x$ podrá asumir cualquiera de los diversos valores 0, 1, 2, 3, 4.
Supongamos que al escribir un trabajo de término para una clase de biología un estudiante necesita especificar la vida promedio, en días, de una mosca doméstica macho. Si no conoce este número de la parte superior de su cabeza, podría representarlo (al menos temporalmente) en su papel con la letra$t$ (que le recuerda el tiempo). Posteriormente, pudo buscar el tiempo promedio en un libro de referencia y encontrarlo ser de 17 días. La letra solo$t$ puede asumir un valor, 17, y ningún otro valor. El valor$t$ es constante.

Definición: Variable, Constante

Una letra o símbolo que representa a cualquier miembro de una colección de dos o más números se denomina variable.
Una letra o símbolo que representa un número específico, conocido o desconocido, se denomina constante.

En el ejemplo 1, la letra$x$ es una variable ya que puede representar cualquiera de los números 0, 1, 2, 3, 4. La letra$t$ ejemplo 2 es una constante ya que sólo puede tener el valor 17.

Números reales

Línea numérica real
El estudio de las matemáticas requiere el uso de varias colecciones de números. La recta numérica real nos permite mostrar visualmente (graficar) los números en los que estamos interesados.

Una línea está compuesta por infinitamente muchos puntos. A cada punto podemos asociar un número único, y con cada número, podemos asociar un punto en particular.

Definición: Coordinar

El número asociado a un punto en la recta numérica se denomina coordenada del punto.

Definición: Graph

El punto en una recta numérica que está asociado a un número determinado se denomina gráfico de ese número.

Construyendo una Línea de Número Real
Construimos una recta numérica real de la siguiente manera:

Dibuja una línea horizontal.
$Una línea horizontal con flechas en el extremo.$
Origen
Elija cualquier punto de la línea y etiquételo 0. A este punto se le llama el origen.
$Una línea horizontal con flechas en el extremo. El centro tiene una marca hash etiquetada como 0.$
Elija una longitud conveniente. A partir de 0, marca esta longitud en ambas direcciones, teniendo cuidado de que las longitudes parezcan que son aproximadamente las mismas.
$Una línea horizontal con flechas en el extremo. El centro tiene una marca hash etiquetada como 0. Hay numerosas marcas hash uniformemente espaciadas a cada lado del cero.$

Ahora definimos un número real.

Definición: Número real

Un número real es cualquier número que es la coordenada de un punto en la línea numérica real.

Definición: Número positivo, números negativos

Los números reales cuyas gráficas están a la derecha de 0 se denominan números reales positivos, o más simplemente, números positivos. Los números reales cuyas gráficas aparecen a la izquierda de 0 se denominan números reales negativos, o más simplemente, números negativos.

$Una línea horizontal con flechas en el extremo. El centro tiene una marca hash etiquetada como 0. En el lado derecho hay un corchete, etiquetado Números positivos. En el lado izquierdo hay un corchete, etiquetado con números negativos.$

El número 0 no es ni positivo ni negativo.

Subconjuntos de números reales

El conjunto de números reales tiene muchos subconjuntos. Algunos de los subconjuntos que son de interés en el estudio del álgebra se enumeran a continuación junto con sus notaciones y gráficas.

Números Naturales, Contando Números
Los números naturales o contando$(N)$: 1, 2, 3, 4,. Lee “y así sucesivamente”.

$Una línea numérica que contiene puntos en las marcas hash para los números uno al siete.$

Números
Enteros Los números enteros$(W)$: 0, 1, 2, 3, 4,.

$Una línea numérica que contiene puntos en las marcas hash para los números del cero al siete.$

Observe que cada número natural es un número entero.

Enteros
Los enteros$(Z)$:.. -3, -2, -1, 0, 1, 2, 3,.

$Una línea numérica que contiene puntos en las marcas hash para los números -4 a 4.$

Observe que cada número entero es un entero.

Números racionales (Fracciones)
Los números racionales$(Q)$: Los números racionales a veces se llaman fracciones. Son números que se pueden escribir como el cociente de dos enteros. Tienen representaciones decimales que terminan o no terminan pero contienen un bloque repetitivo de dígitos. Algunos ejemplos son
$\underbrace{\dfrac{-3}{4} = -0.75}_{text{Terminating}}$$\underbrace{8 \dfrac{11}{27} = 8.407407407...}_{\text{Nonterminating, but repeating.}}$

Algunos números racionales se grafican a continuación.

$Una línea numérica que contiene marcas hash para los números -3 a 4. Hay puntos para tres y octavos negativos, medio negativo, dos quintos, dos divididos por uno, y tres y medio.$

Observe que cada entero es un número racional.

Observe que todavía hay muchos puntos en la recta numérica a los que aún no se les ha asignado un tipo de número. No vamos a examinar estos otros tipos de números en este texto. Se examinan en detalle en álgebra. Un ejemplo de estos números es el número$\pi$, cuya representación decimal no termina ni contiene un bloque repetitivo de dígitos. Una aproximación para$\pi$ es 3.14.

Conjunto de Muestras A

¿Cada número entero es un número natural?

Solución

No. El número 0 es un número entero pero no es un número natural.

Conjunto de Muestras A

¿Hay un entero que no sea un número natural?

Solución

Sí. Algunos ejemplos son 0, -1, -2, -3 y -4.

Conjunto de Muestras A

¿Hay un entero que sea un número entero?

Solución

Sí. De hecho, cada número entero es un entero.

Conjunto de práctica A

¿Cada número natural es un número entero?

Responder: si

Conjunto de práctica A

¿Cada número entero es un número entero?

Responder: si

Conjunto de práctica A

¿Cada entero es un número real?

Responder: si

Conjunto de práctica A

¿Hay un entero que sea un número entero?

Responder: si

Conjunto de práctica A

¿Hay un entero que no sea un número natural?

Responder: si

Pedido de números reales

Ordenar números reales Se dice que
un número real$b$ es mayor que un número real$a$, denotado$b > a$, si$b$ está a la derecha de$a$ en la línea numérica. Así, como cabría esperar,$5 > 2$ ya que 5 está a la derecha de 2 en la recta numérica. También,$-2 > -5$ ya que -2 está a la derecha de -5 en la recta numérica.

Una línea numérica que contiene marcas hash para los números -5 a 5. Hay puntos en las marcas hash para -5, -2, 2 y 5. Por encima del lado izquierdo de la recta numérica se encuentra la expresión -2 -5, y en el lado izquierdo está 5 > 2." data-media-type="image/png" data-print-width="2.5in" width="400" src="https://math.libretexts.org/@api/dek.../graphics9.png">

Si dejamos$a$ y$b$ representamos dos números, entonces$a$ y$b$ se relacionan exactamente de una de tres maneras: O bien

Símbolo de igualdad
$a = b$$a$ y$b$ son iguales (8 = 8)

Símbolos de desigualdad
$\begin{cases} a > b & a \text{ is greater than }b & (8 > 5) \\ a < b & a \text{ is less than } b & (5 < 8) \\ \ & \text{Some variations of these symbols are} & \ \\ a \ne b & a \text{ is not equal to } b & (8 \ne 5) \\ a \ge b & a \text{ is greater than or equal to } b & (a \ge 8) \\ a \le b & a \text{ is less than or equal to } b & (a \le 8) \end{cases}$

Conjunto de Muestras B

¿Qué enteros pueden reemplazar xx para que la siguiente afirmación sea verdadera?

$-3 \le x < 2$

Solución

$Una línea numérica que contiene marcas hash para los números -5 a 5. Hay puntos en las marcas hash para -3, -2, -1, 0, 1.$

Los enteros son -3, -2, -1, 0, 1.

Conjunto de Muestras B

Dibuja una recta numérica que se extienda de -3 a 5. Colocar puntos en todos los números enteros entre -1 y 3 inclusive.

Solución

$Una línea numérica que contiene marcas hash para los números -3 a 5. Hay puntos en las marcas hash para 0, 1, 2 y 3.$

-1 no es un número entero

Set de práctica B

¿Qué enteros pueden reemplazar$x$ para que la siguiente afirmación sea verdadera? $-5 \le x < 2$

Responder: -5, -4, -3, -2, -1, 0

Set de práctica B

Dibuja una recta numérica que se extienda de -4 a 3. Colocar puntos en todos los números naturales entre, pero sin incluir, -2 a 2.

$Una línea horizontal con flechas en el extremo.$

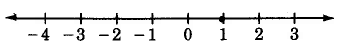
Responder: $Una línea numérica con marcas hash para los números -4 a 3, y un punto en la marca hash para 1.$

Ejercicios

Para los siguientes 8problemas, junto a cada número real, anote todas las colecciones a las que pertenece escribiendo$N$ para número natural,$W$ para número entero o$Z$ para entero. Algunos números pueden pertenecer a más de una colección.

Ejercicio$\PageIndex{1}$

Responder: N, W, Z

Ejercicio$\PageIndex{2}$

Ejercicio$\PageIndex{3}$

Responder: W, Z

Ejercicio$\PageIndex{4}$

Ejercicio$\PageIndex{5}$

-3

Responder: Z

Ejercicio$\PageIndex{6}$

-7

Ejercicio$\PageIndex{7}$

-805

Responder: Z

Ejercicio$\PageIndex{8}$

-900

Ejercicio$\PageIndex{9}$

¿El número 0 es un número positivo, un número negativo, ninguno, o ambos?

Responder: Tampoco

Ejercicio$\PageIndex{10}$

Un entero es un número entero par si es divisible uniformemente por 2. Dibuja una línea numérica que se extienda de -5 a 5 y coloque puntos en todos los enteros pares negativos y todos los enteros impares positivos.

Ejercicio$\PageIndex{11}$

Dibuja una recta numérica que se extienda de -5 a 5. Coloque puntos en todos los enteros que satisfagan$-3 \le x < 4$.

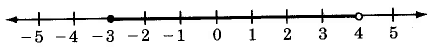
Responder: $Una línea numérica con marcas hash para los números -5 a 5. Hay un punto sólido en la marca hash para -3, un punto abierto en la marca hash para 4. Hay una línea gruesa dibujada entre los puntos de la línea.$

Ejercicio$\PageIndex{12}$

¿Hay un número de dos dígitos más grande? Si es así, ¿qué es?

Ejercicio$\PageIndex{13}$

¿Hay un número más pequeño de dos dígitos? Si es así, ¿qué es?

Responder: Sí, 10

Para los pares de números reales en los siguientes 5 problemas, escriba el símbolo apropiado (<, >, =) en lugar de la □.

Ejercicio$\PageIndex{14}$

-7 □ -2

Ejercicio$\PageIndex{15}$

-5 □ 0

Responder: <

Ejercicio$\PageIndex{16}$

-1 □ 4

Ejercicio$\PageIndex{17}$

6 □ -1

Responder: >

Ejercicio$\PageIndex{18}$

10 □ 10

Para los siguientes 5 problemas, ¿qué números pueden sustituir a m para que las siguientes afirmaciones sean ciertas?

Ejercicio$\PageIndex{19}$

$-1 \le m \le -5$,$m$ un entero.

Responder: {-1, 0, 1, 2, 3, 4, 5}

Ejercicio$\PageIndex{20}$

$-7 < m < -1$,$m$ un entero.

Ejercicio$\PageIndex{21}$

$-3 \le m < 2$,$m$ un número natural.

Responder: {1}

Ejercicio$\PageIndex{22}$

$-15 < m \le -1$,$m$ un número natural.

Ejercicio$\PageIndex{23}$

$-5 \le m < 5$,$m$ un número entero.

Responder: {0, 1, 2, 3, 4}

Para los siguientes 10 problemas, en la recta numérica, ¿cuántas unidades hay entre el par de números dado?

Ejercicio$\PageIndex{24}$

0 y 3

Ejercicio$\PageIndex{25}$

-4 y 0

Responder: 4

Ejercicio$\PageIndex{26}$

-1 y 6

Ejercicio$\PageIndex{27}$

-6 y 2

Responder: 8

Ejercicio$\PageIndex{28}$

-3 y 3

Ejercicio$\PageIndex{29}$

¿Todos los números positivos son mayores que cero?

Responder: si

Ejercicio$\PageIndex{30}$

¿Todos los números positivos son mayores que todos los números negativos?

Ejercicio$\PageIndex{31}$

¿Es 0 mayor que todos los números negativos?

Responder: si

Ejercicio$\PageIndex{32}$

¿Hay un número natural más grande?

Ejercicio$\PageIndex{33}$

¿Hay un entero negativo más grande?

Responder: sí, -1

Ejercicios para revisión

Ejercicio$\PageIndex{34}$

Convertir$6 \dfrac{5}{8}$ a una fracción impropia.

Ejercicio$\PageIndex{35}$

Encuentra el valor:$\dfrac{3}{11}$ de$\dfrac{33}{5}$.

Responder: $\dfrac{9}{5}$$1 \dfrac{4}{5}$o 1.8

Ejercicio$\PageIndex{36}$

Encuentra la suma de$\dfrac{4}{5} + \dfrac{3}{8}$.

Ejercicio$\PageIndex{37}$

Convertir 30.06 cm a m.

Responder: 0.3006 m

Ejercicio$\PageIndex{38}$

Encuentra el área del triángulo.

$Un triángulo con base 16mm y altura 3mm$