10.3: Valor Absoluto

Última actualización
Guardar como PDF

Page ID: 116587

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

entender las definiciones geométricas y algebraicas del valor absoluto

Definición geométrica del valor absoluto

Valor Absoluto-Enfoque
Geométrico Definición geométrica de valor absoluto:
El valor absoluto de un número$a$, denotado$|a|$, es la distancia de a a a 0 en la recta numérica.

El valor absoluto responde a la pregunta de “hasta dónde” y no “de qué manera”. La frase “qué tan lejos” implica “longitud” y la longitud es siempre una cantidad no negativa. Así, el valor absoluto de un número es un número no negativo.

Conjunto de Muestras A

Determinar cada valor.

$|4| = 4$

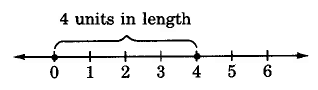
$Una línea numérica con marcas hash de 0 a 6, con cero a 4 marcadas como 4 unidades de longitud.$

Conjunto de Muestras A

$|-4| = 4$

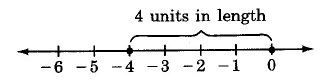
$Una línea numérica con marcas hash de -6 a 0, con -4 a 0 marcadas como 4 unidades de longitud.$

Conjunto de Muestras A

$|0| = 0$

Conjunto de Muestras A

$-|5| = -5$. La cantidad en el lado izquierdo del signo igual se lee como “negativa el valor absoluto de 5”. El valor absoluto de 5 es 5. De ahí que negativo el valor absoluto de 5 sea -5.

Conjunto de Muestras A

$-|-3| = -3$. La cantidad en el lado izquierdo del signo igual se lee como “negativa el valor absoluto de -3”. El valor absoluto de -3 es 3. De ahí que negativo el valor absoluto de -3 sea$-(3) = -3$.

Conjunto de práctica A

Razonando geométricamente, determinar cada valor absoluto.

$|7|$

Contestar: 7

Conjunto de práctica A

$|-3|$

Contestar: 3

Conjunto de práctica A

$|12|$

Contestar: 12

Conjunto de práctica A

$|0|$

Contestar: 0

Conjunto de práctica A

$-|9|$

Contestar: -9

Conjunto de práctica A

$-|-6|$

Contestar: -6

Definición algebraica del valor absoluto

A partir de los problemas del Conjunto de Muestras A, podemos sugerir la siguiente definición algebraica de valor absoluto. Tenga en cuenta que la definición tiene dos partes.

Valor absoluto: enfoque algebraico Definición
algebraica del valor absoluto
El valor absoluto de un número a es

$|a| = \begin{cases} a, & \text{ if } a \ge 0 \\ -a, & \text{ if } a < 0 \end{cases}$

La definición algebraica toma en cuenta el hecho de que el número aa podría ser positivo o cero$(a \ge 0)$ o negativo$(a < 0)$.

Si el número$a$ es positivo o cero$(a \ge 0)$, se aplica la parte superior de la definición. La parte superior de la definición nos dice que si el número encerrado en las barras de valor absoluto es un número no negativo, el valor absoluto del número es el número mismo.
La parte inferior de la definición nos dice que si el número encerrado dentro de las barras de valor absoluto es un número negativo, el valor absoluto del número es el opuesto del número. Lo contrario de un número negativo es un número positivo.

Nota

La definición dice que las líneas verticales de valor absoluto pueden eliminarse sólo si sabemos si el número interior es positivo o negativo.

Conjunto de Muestras B

Utilice la definición algebraica de valor absoluto para encontrar los siguientes valores.

$|8|$. El número encerrado dentro de las barras de valor absoluto es un número no negativo, por lo que se aplica la parte superior de la definición. Esta parte dice que el valor absoluto de 8 es el propio 8.

$|8| = 8$

Conjunto de Muestras B

$|-3|$. El número encerrado dentro de las barras de valor absoluto es un número negativo, por lo que se aplica la parte inferior de la definición. Esta parte dice que el valor absoluto de -3 es el opuesto de -3, que es$-(-3)$. Por la definición de valor absoluto y la propiedad doble negativa,

$|-3| = -(-3) = 3$

Set de práctica B

Utilice la definición algebraica de valor absoluto para encontrar los siguientes valores.

$|7|$

Contestar: 7

Set de práctica B

$|9|$

Contestar: 9

Set de práctica B

$|-12|$

Contestar: 12

Set de práctica B

$|-5|$

Contestar: 5

Set de práctica B

$-|8|$

Contestar: -8

Set de práctica B

$-|1|$

Contestar: -1

Set de práctica B

$-|-52|$

Contestar: -52

Set de práctica B

$-|-31|$

Contestar: -31

Ejercicios

Determinar cada uno de los valores.

Ejercicio$\PageIndex{1}$

$|5|$

Contestar: 5

Ejercicio$\PageIndex{2}$

$|3|$

Ejercicio$\PageIndex{3}$

$|6|$

Contestar: 6

Ejercicio$\PageIndex{4}$

$|-9|$

Ejercicio$\PageIndex{5}$

$|-1|$

Contestar: 1

Ejercicio$\PageIndex{6}$

$|-4|$

Ejercicio$\PageIndex{7}$

$-|3|$

Contestar: -3

Ejercicio$\PageIndex{8}$

$-|7|$

Ejercicio$\PageIndex{9}$

$-|-14|$

Contestar: -14

Ejercicio$\PageIndex{10}$

$|0|$

Ejercicio$\PageIndex{11}$

$|-26|$

Contestar: 26

Ejercicio$\PageIndex{12}$

$-|-26|$

Ejercicio$\PageIndex{13}$

$-(-|4|)$

Contestar: 4

Ejercicio$\PageIndex{14}$

$-(-|2|)$

Ejercicio$\PageIndex{15}$

$-(-|-6|)$

Contestar: 6

Ejercicio$\PageIndex{16}$

$-(-|-42|)$

Ejercicio$\PageIndex{17}$

$|5| - |-2|$

Contestar: 3

Ejercicio$\PageIndex{18}$

$|-2|^3$

Ejercicio$\PageIndex{19}$

$-|(2 \cdot 3)|$

Contestar: 6

Ejercicio$\PageIndex{20}$

$|-2| - |-9|$

Ejercicio$\PageIndex{21}$

$(|-6| + |4|)^2$

Contestar: 100

Ejercicio$\PageIndex{22}$

$(|-1| - |1|)^3$

Ejercicio$\PageIndex{23}$

$(|4| + |-6|)^2 - (|-2|)^3$

Contestar: 92

Ejercicio$\PageIndex{24}$

$-[|-10| - 6]^2$

Ejercicio$\PageIndex{25}$

$-\{-[-|-4| + |-3|]^3\}^2$

Contestar: -1

Ejercicio$\PageIndex{26}$

Un Oficial de Control de Misión en Cabo Cañaveral hace la declaración “despegue, T menos 50 segundos”. ¿Cuánto tiempo falta antes del despegue?

Ejercicio$\PageIndex{27}$

Debido a una desaceleración en la industria, una compañía informática de Silicon Valley se encuentra en deuda de 2.400,000 dólares. Utilice la notación de valor absoluto para describir la deuda de esta compañía.

Contestar: -$|-2,400,000|

Ejercicio$\PageIndex{28}$

Una máquina en particular se ajusta correctamente si al actuar su medidor lee 0. Una máquina en particular tiene una lectura de medidor de -1.6 al actuar. ¿A qué distancia está esta máquina de su ajuste correcto?

Ejercicios para la revisión

Ejercicio$\PageIndex{29}$

Encuentra la suma:$\dfrac{9}{70} + \dfrac{5}{21} + \dfrac{8}{15}$.

Contestar: $\dfrac{9}{10}$

Ejercicio$\PageIndex{30}$

Encuentra el valor de$\dfrac{\dfrac{3}{10} + \dfrac{4}{12}}{\dfrac{19}{20}}$.

Ejercicio$\PageIndex{31}$

Convertir$3.2 \dfrac{3}{5}$ a una fracción

Contestar: $3 \dfrac{13}{50}$o$\dfrac{163}{50}$

Ejercicio$\PageIndex{32}$

La proporción de ácido a agua en una solución es$\dfrac{3}{8}$. ¿Cuántos mL de ácido hay en una solución que contiene 112 mL de agua?

Ejercicio$\PageIndex{33}$

Encuentra el valor de$-6 - (-8)$.

Contestar: 2