1.2: Sumando y restando números enteros
- Page ID
- 113396
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la expresión 3 + 4, que muestra la suma de dos números enteros, los números enteros 3 y 4 se denominan adiciones o términos. Podemos utilizar un enfoque visual para encontrar la suma de 3 y 4. Primero, construya una recta numérica como se muestra en la Figura 1.2.
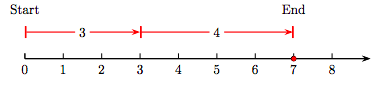
Para agregar 3 y 4, proceder de la siguiente manera.
- Comienza en el número 0, luego dibuja una flecha 3 unidades a la derecha, como se muestra en la Figura 1.2. Esta flecha tiene magnitud (longitud) tres y representa el número entero 3.
- Dibuja una segunda flecha de longitud cuatro, comenzando por el final de la primera flecha que representa el número 3. Esta flecha tiene magnitud (longitud) cuatro y representa el número entero 4.
- La suma de 3 y 4 podría estar representada por una flecha que inicia en el número 0 y termina en el número 7. Sin embargo, preferimos marcar esta suma en la recta numérica como un punto sólido en todo el número 7. Este número representa la suma de los números enteros 3 y 4.
La propiedad conmutativa de la adición
Cambiemos el orden en el que sumamos los números enteros 3 y 4. Es decir, encontremos la suma 4 + 3 en su lugar.
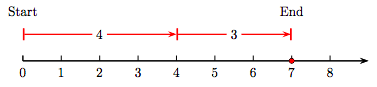
Como puede ver en la Figura 1.3, comenzamos en cero luego dibujamos una flecha de longitud cuatro, seguida de una flecha de longitud tres. Sin embargo, el resultado es el mismo; es decir, 4 + 3 = 7.
Así, el orden en que sumamos tres y cuatro no importa; es decir,
3 + 4=4 + 3.
Esta propiedad de adición de números enteros se conoce como la propiedad conmutativa de la adición.
La propiedad conmutativa de la adición
Que a y b representen dos números enteros. Entonces,
a + b = b + a.
Agrupación de símbolos
En matemáticas, utilizamos símbolos de agrupación para afectar el orden en que se evalúa una expresión. Ya sea que usemos paréntesis, corchetes o llaves, la expresión dentro de cualquier par de símbolos de agrupación debe evaluarse primero. Por ejemplo, anote cómo evaluamos primero la suma entre paréntesis en el siguiente cálculo.
(3 + 4) + 5 = 7 + 5
= 12
La regla es simple: Lo que esté dentro de los paréntesis se evalúa primero.
Redacción Matemáticas
Al escribir declaraciones matemáticas, siga el mantra:
Un signo igual por línea.
Podemos usar corchetes en lugar de paréntesis.
5 + [7 + 9] = 5 + 16
= 21
Nuevamente, anote cómo se evalúa primero la expresión dentro de los corchetes.
También podemos usar llaves en lugar de paréntesis o corchetes.
{2+3} + 4 = 5 + 4
= 9
Nuevamente, observe cómo se evalúa primero la expresión dentro de las llaves.
Si los símbolos de agrupación están anidados, primero evaluamos los paréntesis más internos.
Por ejemplo,
2 + [3 + (4 + 5)] = 2 + [3 + 9]
= 2 + 12
= 14.
Agrupación de símbolos
Use paréntesis, corchetes o llaves para delimitar primero la parte de una expresión que desea evaluar. Si los símbolos de agrupación están anidados, evalúe primero la expresión en el par más interno de símbolos de agrupación.
La propiedad asociativa de la adición
Considerar la evaluación de la expresión (2+3) +4. Primero evaluamos la expresión entre paréntesis.
(2 + 3) + 4 = 5 + 4
= 9
Ahora, supongamos que cambiamos el orden de adición a 2 + (3 + 4). Entonces,
2 + (3 + 4) = 2 + 7
= 9.
Si bien la agrupación ha cambiado, el resultado es el mismo. Es decir,
(2 + 3) + 4 = 2 + (3 + 4).
Esta propiedad de suma de números enteros se denomina propiedad asociada de suma.
Propiedad Asociada de Adición
Que a, b y c representen números enteros. Entonces,
(a + b) + c = a + (b + c).
Debido a la propiedad asociada de suma, cuando se presenta con una suma de tres números, ya sea que empieces sumando los dos primeros números o los dos últimos números, la suma resultante es la misma.
La identidad aditiva
Imagine una visualización numérica de la suma de cuatro y cero; es decir, 4 + 0.
En la Figura 1.4, comenzamos en cero, luego dibujamos una flecha de magnitud (longitud) cuatro apuntando a la derecha. Ahora, al final de esta flecha, adjuntar una segunda flecha de longitud cero. Desde luego, eso significa que permanecemos justo donde estamos, a las 4. De ahí que el punto sombreado en 4 sea la suma. Es decir, 4 + 0 = 4.
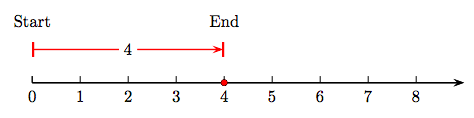
La propiedad de identidad aditiva
El número entero cero se llama identidad aditiva. Si a es cualquier número entero, el
a + 0 = a.
El número cero se llama identidad aditiva porque si agregas cero a cualquier número, recuperas el número idéntico.
Sumando números enteros más grandes
Para completar, incluimos dos ejemplos de sumar números enteros más grandes. Esperemos que el algoritmo sea familiar a partir de cursos anteriores.
Ejemplo 1
Simplificar: 1, 234 + 498.
Solución
Alinee los números verticalmente, luego agregue, comenzando en la columna más alejada a la derecha. Suma los dígitos en la columna unos, 4 + 8 = 12. Escribe el 2, luego lleva un 1 a la columna de decenas. A continuación, agrega los dígitos en la columna de decenas, 3 + 9 = 12, agrega el acarreo para obtener 13, luego escribe el 3 y lleva un 1 a la columna de cientos. Continuar de esta manera, trabajando de derecha a izquierda
\( \begin{array}{r}{11} \\ {1234} \\ {+\quad 498} \\ \hline 1732\end{array}\)
Por lo tanto, 1, 234 + 498 = 1, 732
Ejercicio
Simplificar: 1,286 + 349.
- Contestar
-
1635
Sumar tres o más números de la misma manera.
Ejemplo 2
Simplifica: 256 + 322 + 418.
Solución
Alinee los números verticalmente, luego agregue, comenzando en la columna más alejada a la derecha. Suma los dígitos en la columna unos, 6 + 2 + 8 = 16. Escribe el 6, luego lleva un 1 a la columna de decenas. Continuar de esta manera, trabajando de derecha a izquierda.
\( \begin{array}{r}{256} \\ {322} \\ {+418} \\ \hline 996\end{array}\)
Por lo tanto, 256 + 322 + 418 = 996.
Ejercicio
Simplificar: 256 + 342 + 283
- Contestar
-
881
Resta de Números Enteros
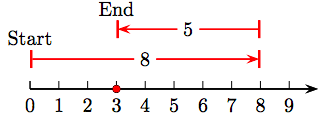
La idea clave es esta: La resta es lo opuesto a la suma. Por ejemplo, considere la diferencia 7 - 4 representada en la recta numérica en la Figura 1.5.
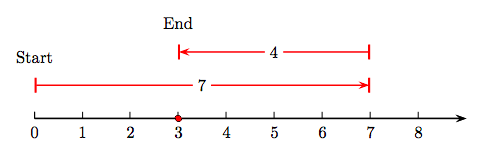
Si estuviéramos sumando 7 y 4, primero dibujamos una flecha comenzando en cero apuntando a la derecha con magnitud (longitud) siete. Entonces, para sumar 4, dibujaríamos una segunda flecha de magnitud (longitud) 4, unida al final de la primera flecha y apuntando a la derecha.
No obstante, debido a que la resta es lo opuesto a la suma, en la Figura 1.5 adjuntamos una flecha de magnitud (longitud) cuatro al final de la primera flecha, pero apuntando en sentido contrario (a la izquierda). Tenga en cuenta que esta última flecha termina en la respuesta, que es un punto sombreado en la línea numérica en 3. Es decir, 7 − 4 = 3.
Tenga en cuenta que la resta no es conmutativa; es decir, no tiene sentido decir que 7 − 5 es lo mismo que 5 − 7.
La resta no es asociativa. No es el caso de que (9 − 5) − 2 sea lo mismo que 9 − (5 − 2). Por un lado,
(9 − 5) − 2 = 4 − 2
= 2,
pero
9 − (5 − 2) = 9 − 3
= 6.
Restar números enteros más grandes
Al igual que hicimos con sumar números enteros más grandes, para restar dos números enteros grandes, alinearlos verticalmente luego restar, trabajando de derecha a izquierda. Es posible que tengas que “pedir prestado” para completar la resta en cualquier paso.
Ejemplo 3
Simplificar: 1, 755 − 328.
Solución
Alinea los números verticalmente, luego resta, comenzando en la columna ones, luego trabajando de derecha a izquierda. En la columna unos, no podemos restar 8 de 5, así que tomamos prestado de la columna anterior. Ahora, 8 de 15 es 7. Continuar de esta manera, trabajando de derecha a izquierda.
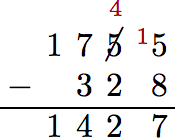
Por lo tanto, 1, 755 − 328 = 1, 427.
Ejercicio
Simplificar: 5,635 - 288.
- Contestar
-
5,347
Orden de Operaciones
A falta de símbolos de agrupación, es importante entender que la suma no tiene precedencia sobre la resta, y viceversa.
Realizar todas las sumas y restaciones en el orden presentado, moviéndose de izquierda a derecha.
Veamos un ejemplo.
Ejemplo 4
Simplifica la expresión\(15 − 8 + 4\).
Solución
Este ejemplo puede ser más complicado de lo que parece. No obstante, si seguimos la regla (realizamos todas las adiciones y restaciones en el orden presentado, moviéndonos de izquierda a derecha), no deberíamos tener problemas. Primero viene quince menos ocho, que es siete. Entonces siete más cuatro son once.
\[\begin{align*}15 − 8 + 4 &= 7 + 4 \\[4pt] &= 11. \end{align*}\]
Ejercicio
Simplificar:\(25 − 10 + 8\).
- Contestar
-
23
¡Precaución! ¡Respuesta incorrecta por delante!
Tenga en cuenta que es posible llegar a una respuesta diferente (pero incorrecta) si favorecemos la suma sobre la resta en el Ejemplo 4. Si primero sumamos ocho y cuatro, entonces 15 − 8 + 4 se convierte en 15 − 12, que es 3. No obstante, tenga en cuenta que esto es incorrecto, porque viola la regla “realizar todas las adiciones y restaciones en el orden presentado, moviéndose de izquierda a derecha”.
Aplicaciones — Geometría
Hay cualquier número de aplicaciones que requieren una suma o diferencia de números enteros. Examinemos algunos del mundo de la geometría.
Perímetro de un Polígono
En geometría un polígono es una figura plana compuesta por una trayectoria cerrada de una secuencia finita de segmentos. Los segmentos se llaman los bordes o lados del polígono y los puntos donde dos bordes se encuentran se llaman los vértices del polígono. El perímetro de cualquier polígono es la suma de las longitudes de sus lados.
Ejemplo 5
Un cuadrilátero es un polígono con cuatro lados. Encuentra el perímetro del cuadrilátero que se muestra a continuación, donde se miden los lados a continuación.
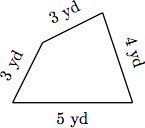
Solución
Para encontrar el perímetro del cuadrilátero, encuentra la suma de las longitudes de los costados.
Perímetro = 3 + 3 + 4 + 5 = 15
De ahí que el perímetro del cuadrilátero sea de 15 yardas.
Ejercicio
Un cuadrilátero tiene lados que miden en 4 in., 3 in., 5 in., y 5 in. Encuentra el perímetro.
- Contestar
-
17 pulgadas
Ejemplo 6
Un cuadrilátero (cuatro lados) es un rectángulo si sus cuatro ángulos son ángulos rectos. Se puede demostrar que los lados opuestos de un rectángulo deben ser iguales. Encuentra el perímetro del rectángulo que se muestra a continuación, donde los lados del rectángulo se miden en metros.
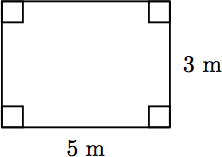
Solución
Para encontrar el perímetro del rectángulo, encuentra la suma de los cuatro lados. Debido a que los lados opuestos tienen la misma longitud, tenemos dos lados de longitud 5 metros y dos lados de longitud 3 metros. Por lo tanto,
Perímetro = 5 + 3 + 5 + 3 = 16.
Así, el perímetro del rectángulo es de 16 metros.
Ejercicio
Un rectángulo tiene longitud 12 metros y ancho 8 metros. Encuentra su perímetro.
- Contestar
-
40 metros
Ejemplo 7
Un cuadrilátero (cuatro lados) es un cuadrado si sus cuatro lados miden 18 centímetros. Encuentra su perímetro. son iguales y los cuatro de sus ángulos son ángulos rectos. En la foto de abajo hay un cuadrado que tiene un lado de largo 12 pies. Encuentra el perímetro de la plaza.
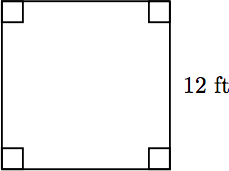
Solución
Debido a que el cuadrilátero es un cuadrado, los cuatro lados tienen la misma longitud, es decir, 12 pies. Para encontrar el perímetro de la plaza, encuentra la suma de los cuatro lados. Perímetro = 12 + 12 + 12 + 12 = 48
De ahí que el perímetro de la plaza sea de 48 pies.
Ejercicio
Un cuadrado tiene un lado que mide 18 centímetros. Encuentra su perímetro.
- Contestar
-
72 centímetros
Aplicación — Combustibles Alternativos
Los automóviles que funcionan con combustibles alternativos (distintos a la gasolina) han aumentado en Estados Unidos a lo largo de los años.
Ejemplo 8
En el cuadro 1.2 se muestra el número de automóviles (en miles) que funcionan con gas natural comprimido versus el año. Cree un gráfico de barras que muestre el número de autos que funcionan con gas natural comprimido versus el año.
| Año | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| Número | 23 | 32 | 4` | 50 | 60 | 73 | 78 | 89 | 101 |
Cuadro 1.2: Número de vehículos (en miles) que funcionan con gas natural comprimido.
Solución
Colocar los años en el eje horizontal. En cada año, dibuje una barra que tenga una altura igual al número de autos en ese año que funcionan con gas natural comprimido. Escala el eje vertical en miles.
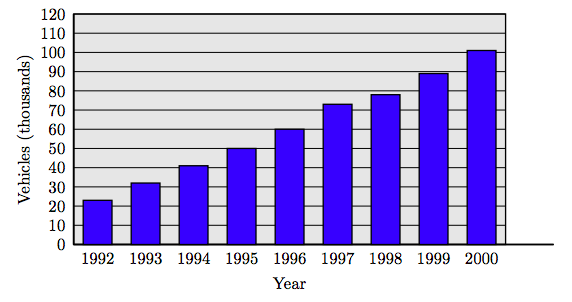
Ejercicio
En la siguiente tabla se muestra el número de autos híbridos (en miles) por país.
| País | Número |
| U.S. | 279 |
| Japón | 77 |
| Canadá | 17 |
| U.K. | 14 |
| Países Bajos | 11 |
Crear un gráfico de barras que muestre el número de autos versus el país de uso.
Ejemplo 9
Usando los datos del Cuadro 1.2, pliegue una tabla que muestre las diferencias en años consecutivos, luego cree una gráfica lineal del resultado. ¿En qué años consecutivos Estados Unidos vio el mayor incremento de autos propulsados por gas natural comprimido?
Solución
En el Cuadro 1.3 se muestran las diferencias en años consecutivos.
A continuación, elabora una gráfica de líneas. Colocar años consecutivos en el eje horizontal. En cada par de años consecutivos, trazar un punto a una altura igual a la diferencia en vehículos de combustible alternativo. Conecte los puntos con segmentos de línea recta.
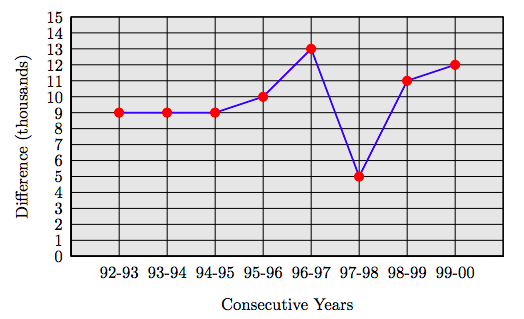
Obsérvese cómo el gráfico de líneas deja completamente claro que el mayor incremento en vehículos propulsados por gas natural comprimido ocurrió en los años consecutivos 1996-1997, un incremento de 13 mil vehículos.
Ejercicio
En la siguiente tabla se muestran las puntuaciones porcentuales de Alfonso en sus exámenes de matemáticas.
| Examen | Porcentaje |
| Examen #1 | 52 |
| Examen #2 | 45 |
| Examen #3 | 72 |
| Examen #4 | 889 |
| Examen #5 | 76 |
Construir una gráfica lineal de las puntuaciones de los exámenes de Alphonso versus el número de examen.
Ejercicios
1. Esboce un diagrama de líneas numéricas que represente la suma 3 + 2, como se muestra en la Figura 1.2 en la narrativa de esta sección.
2. Esboce un diagrama de líneas numéricas que represente la suma de 3 + 5, como se muestra en la Figura 1.2 en la narrativa de esta sección.
3. Esboce un diagrama de líneas numéricas que represente la suma de 3 + 4, como se muestra en la Figura 1.2 en la narrativa de esta sección.
4. Esboce un diagrama de líneas numéricas que represente la suma 2 + 4, como se muestra en la Figura 1.2 en la narrativa de esta sección.
5. Esboce un diagrama de líneas numéricas que represente la suma 4 + 2, como se muestra en la Figura 1.2 en la narrativa de esta sección.
6. Esboce un diagrama de líneas numéricas que represente la suma 4 + 3, como se muestra en la Figura 1.2 en la narrativa de esta sección.
7. Esboce un diagrama de líneas numéricas que represente la suma 2 + 5, como se muestra en la Figura 1.2 en la narrativa de esta sección.
8. Esboce un diagrama de líneas numéricas que represente la suma de 4 + 5, como se muestra en la Figura 1.2 en la narrativa de esta sección.
9. Esboce un diagrama de líneas numéricas que represente la suma 4 + 4, como se muestra en la Figura 1.2 en la narrativa de esta sección.
10. Esboce un diagrama de líneas numéricas que represente la suma 3 + 3, como se muestra en la Figura 1.2 en la narrativa de esta sección.
En los Ejercicios 11-28, determinar qué propiedad de adición está representada por la identidad dada
11. 28 + 0 = 28
12. 53 + 0 = 53
13. 24 + 0 = 24
14. 93 + 0 = 93
15. (51 + 66) + 88 = 51 + (66 + 88)
16. (90 + 96) + 4 = 90 + (96 + 4)
17. 64 + 39 = 39 + 64
18. 68 + 73 = 73 + 68
19. (70 + 27) + 52 = 70 + (27 + 52)
20. (8 + 53) + 81 = 8 + (53 + 81)
21. 79 + 0 = 79
22. 42 + 0 = 42
23. 10 + 94 = 94 + 10
24. 55 + 86 = 86 + 55
25. 47 + 26 = 26 + 47
26. 62 + 26 = 26 + 62
27. (61 + 53) + 29 = 61 + (53 + 29)
28. (29 + 96) + 61 = 29 + (96 + 61)
29. Esboce un diagrama de líneas numéricas que represente la diferencia 8−2, como se muestra en la Figura 1.5 en la narrativa de esta sección.
30. Esboce un diagrama de líneas numéricas que represente la diferencia 8−4, como se muestra en la Figura 1.5 en la narrativa de esta sección.
31. Esboce un diagrama de líneas numéricas que represente la diferencia 7−2, como se muestra en la Figura 1.5 en la narrativa de esta sección.
32. Esboce un diagrama de líneas numéricas que represente la diferencia 9−5, como se muestra en la Figura 1.5 en la narrativa de esta sección.
33. Esboce un diagrama de líneas numéricas que represente la diferencia 7−4, como se muestra en la Figura 1.5 en la narrativa de esta sección.
34. Esboce un diagrama de líneas numéricas que represente la diferencia 6−4, como se muestra en la Figura 1.5 en la narrativa de esta sección.
35. Esboce un diagrama de líneas numéricas que represente la diferencia 9−4, como se muestra en la Figura 1.5 en la narrativa de esta sección.
36. Esboce un diagrama de líneas numéricas que represente la diferencia 6−5, como se muestra en la Figura 1.5 en la narrativa de esta sección.
37. Esboce un diagrama de líneas numéricas que represente la diferencia 8−5, como se muestra en la Figura 1.5 en la narrativa de esta sección.
38. Esboce un diagrama de líneas numéricas que represente la diferencia 9−3, como se muestra en la Figura 1.5 en la narrativa de esta sección.
En los Ejercicios 39-50, simplificar la expresión dada.
39. 16 − 8+2
40. 17 − 3+5
41. 20 − 5 + 14
42. 14 − 5+6
43. 15 − 2+5
44. 13 − 4+2
45. 12 − 5+4
46. 19 − 4 + 13
47. 12 − 6+4
48. 13 − 4 + 18
49. 15 − 5+8
50. 13 − 3 + 11
En los Ejercicios 51-58, se dan el ancho W y el largo L de un rectángulo. Encuentra el perímetro P del rectángulo.
51. W = 7 in, L = 9 in
52. W = 4 in, L = 6 in
53. W = 8 in, L = 9 in
54. W = 5 in, L = 9 in
55. Ancho = 4 cm, L = 6 cm
56. W = 5 in, L = 8 in
57. Ancho = 4 cm, L = 7 cm
58. W = 4 in, L = 9 in
En los Ejercicios 59-66, se da la longitud s de un lado de un cuadrado. Encuentra el perímetro P de la plaza.
59. s = 25 cm
60. s = 21 in
61. s = 16 cm
62. s = 10 in
63. s = 18 in
64. s = 7 in
65. s = 3 in
66. s = 20 in
En Ejercicios 67-86, encuentra la suma.
67. 3005 + 5217
68. 1870 + 5021
69. 575 + 354 + 759
70. 140 + 962 + 817
71. 472 + (520 + 575)
72. 318 + (397 + 437)
73. 274 + (764 + 690)
74. 638 + (310 + 447)
75. 8583 + 592
76. 5357 + 9936
77. 899 + 528 + 116
78. 841 + 368 + 919
79. (466 + 744) + 517
80. (899 + 996) + 295
81. 563 + 298 + 611 + 828
82. 789 + 328 + 887 + 729
83. 607 + 29 + 270 + 245
84. 738 + 471 + 876 + 469
85. (86 + 557) + 80
86. (435 + 124) + 132
En Ejercicios 87-104, encuentra la diferencia.
87. 3493 − 2034 − 227
88. 3950 − 1530 − 2363
89. 8338 − 7366
90. 2157 − 1224
91. 2974 − 2374
92. 881 − 606
93. 3838 − (777 − 241)
94. 8695 − (6290 − 4233)
95. 5846 − 541 − 4577
96. 5738 − 280 − 4280
97. 3084 − (2882 − 614)
98. 1841 − (217 − 28)
99. 2103 − (1265 − 251)
100. 1471 − (640 − 50)
101. 9764 − 4837 − 150
102. 9626 − 8363 − 1052
103. 7095 − 226
104. 4826 − 1199
105. Subsidios de Agua. Desde que comenzó la sequía en 2007, las granjas de California han recibido 79 millones de dólares en subsidios de agua. Los productores de algodón y arroz de California recibieron 439 millones de dólares adicionales. ¿Cuánto subsidio total de agua han recibido los agricultores? Horarios de Prensa Asociados-Estándar 4/15/09
106. Presupuesto de Guerra. El presupuesto federal de 2010 destina 534 mil millones de dólares para los programas base del Departamento de Defensa y 130 mil millones adicionales para las dos guerras de la nación. ¿Cuánto recibirá en conjunto el Departamento de Defensa? Tiempos de Prensa Asociados Estándar 5/8/09
107. Sol Helado. Arcata, CA es el hogar de Sun Frost, un fabricante de refrigeradores y congeladores altamente eficientes. El refrigerador/congelador modelo AC RF12 cuesta $2,279 mientras que un refrigerador/congelador modelo R16 cuesta $3,017. ¿Cuánto más cuesta el modelo R16? Fuente: www.sunfrost.com/retail pricelist.htm l
108. Órbita Transbordador. El transbordador espacial generalmente orbita a 250 millas sobre la superficie de la tierra. Para dar servicio al Telescopio Espacial Hubble, el transbordador tuvo que ir a 350 millas sobre la superficie. ¿Cuánto más alto tuvo que orbitar el transbordador?
109. Órbita de la Tierra. La Tierra orbita al sol en una elipse. Cuando la tierra está en su punto más cercano al sol, llamado perihelio, la tierra es de unos 147 millones de kilómetros. Cuando la tierra se encuentra en su punto más alejado del sol, llamado afelio, la tierra se encuentra a unos 152 millones de kilómetros del sol. ¿Cuál es la diferencia en millones de kilómetros entre el afelio y el perihelio?
110. Órbita de Plutón. La órbita de Plutón es altamente excéntrica. Encuentra la diferencia entre el acercamiento más cercano de Plutón al sol y la distancia más alejada de Plutón del sol si el perihelio de Plutón (el punto más cercano en su órbita alrededor del sol) es de unos 7 mil millones de kilómetros y su afelio (el punto más alejado de su órbita alrededor del sol) es de unos 30 mil millones de kilómetros.
111. Temperatura de Manchas Solares. La superficie del sol es de unos 10,000 grados Fahrenheit. Las manchas solares son regiones más oscuras en la superficie del sol que tienen una temperatura relativamente más fría de 6,300 grados Fahrenheit. ¿Cuántos grados más frías son las manchas solares?
112. Trabajos. The Times-Standard informa que durante el próximo año, el negocio de procesamiento de tarjetas de crédito y débito Humboldt Merchant Services espera recortar 36 de sus 80 empleos, pero luego dar la vuelta y contratar otros 21. ¿Cuánta gente va a estar trabajando para la empresa entonces? Times-Standard 5/6/09
113. Tigres salvajes. El gráfico muestra la población estimada de tigres salvajes, por región. Según esta tabla, ¿cuál es la población total de tigres salvajes a nivel mundial? Associated Press-Times-Standard 01/24/10 Monturas de presión para salvar al tigre.
| Región | Población de tigres |
| India, Nepal y Bután | 1650 |
| China y Rusia | 450 |
| Bangladesh | 250 |
| Sumatra | 400 |
| Malasia | 500 |
| otros SE Asia | 350 |
114. Ataques Piratas. El siguiente gráfico de barras rastrea los ataques piratas frente a las costas de Somalia.
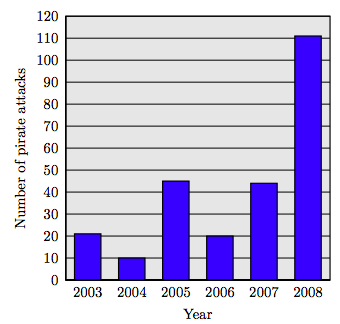
Fuente: ICC International Maritime Bureau, AP Times-Standard, 4/15/2009
a) ¿Cuántos ataques piratas hubo en 2003, 2004 y 2005 combinados?
b) ¿Cuántos ataques piratas hubo en 2006, 2007 y 2008 combinados?
c) ¿Cuántos ataques piratas más hubo en 2008 que en 2007?
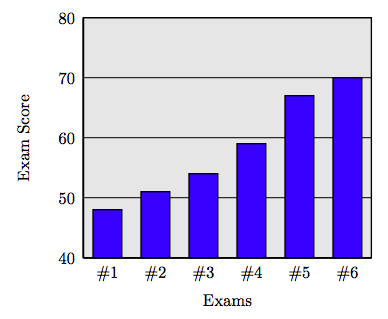
115. Emily muestra mejoría en cada examen sucesivo a lo largo del término. Sus puntajes de exámenes se registran en la siguiente tabla.
| Examen | Score |
| Examen #1 | 48 |
| Examen #2 | 51 |
| Examen #3 | 54 |
| Examen #4 | 59 |
| Examen #5 | 67 |
| Examen #6 | 70 |
a) Crear una parcela de barras para los puntajes de los exámenes de Emily. Colocar los números de examen en el eje horizontal en el mismo orden que se muestra en la tabla anterior.
b) Crear una tabla que muestre diferencias sucesivas en los puntajes de los exámenes. Haz una gráfica lineal de estas diferencias. ¿Entre qué dos exámenes mostró Emily la mayor mejora?
116. Jason muestra mejoría en cada examen sucesivo a lo largo del término. Sus puntajes de exámenes se registran en la siguiente tabla.
| Examen | Score |
| Examen #1 | 34 |
| Examen #2 | 42 |
| Examen #3 | 45 |
| Examen #4 | 50 |
| Examen #5 | 57 |
| Examen #6 | 62 |
a) Crear una parcela de barras para los puntajes de los exámenes de Jason. Colocar los números de examen en el eje horizontal en el mismo orden que se muestra en la tabla anterior.
b) Crear una tabla que muestre diferencias sucesivas en los puntajes de los exámenes. Haz una gráfica lineal de estas diferencias. ¿Entre qué dos exámenes mostró Jason la mayor mejora?
RESPUESTAS
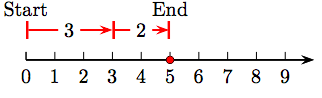
1. 3 + 2 = 5.
3. 3 + 4 = 7.
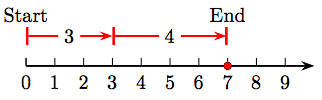
5. 4 + 2 = 6.
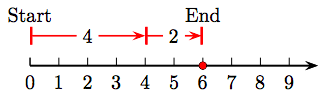
7. 2 + 5 = 7.
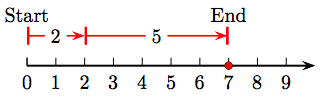
9. 4 + 4 = 8.
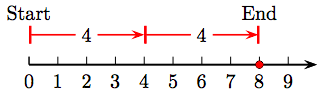
11. Identidad aditiva propiedad de adición.
13. Identidad aditiva propiedad de adición.
15. Propiedad asociativa de adición
17. Propiedad conmutativa de adición
19. Propiedad asociativa de adición
21. Identidad aditiva propiedad de adición.
23. Propiedad conmutativa de adición
25. Propiedad conmutativa de adición
27. Propiedad asociativa de adición
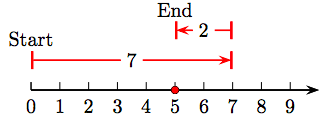
29. 8 − 2 = 6.
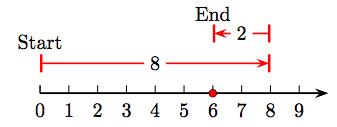
31. 7 − 2 = 5.
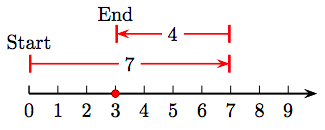
33. 7 − 4 = 3.
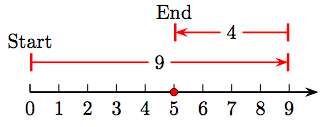
35. 9 − 4 = 5.
37. 8 − 5 = 3.
39. 10
41. 29
43. 18
45. 11
47. 10
49. 18
51. P = 32 in
53. P = 34 in
55. P = 20 cm
57. P = 22 cm
59. P = 100 cm
61. P = 64 cm
63. P = 72 in
65. P = 12 in
67. 8222
69. 1688
71. 1567
73. 1728
75. 9175
77. 1543
79. 1727
81. 2300
83. 1151
85. 723
87. 1232
89. 972
91. 600
93. 3302
95. 728
97. 816
99. 1089
101. 4777
103. 6869
105. 518 millones de dólares
107. $738
109. 5 millones de kilómetros
111. 3,700 grados Fahrenheit
113. 3600
115. a) Gráfico de barras.
b) Gráfica lineal de diferencias consecutivas. La gráfica lineal de diferencias consecutivas en la puntuación del examen.
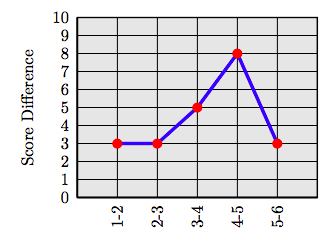
La mayor mejora estuvo entre el Examen #4 y el Examen #5, donde Emily mejoró en 8 puntos.