1.3: Multiplicación y división de números enteros
- Page ID
- 113403
Comenzamos esta sección discutiendo la multiplicación de números enteros. El primer orden del día es introducir los diversos símbolos utilizados para indicar la multiplicación de dos números enteros.
Símbolos matemáticos que indican multiplicación
| Símbolo | Ejemplo | |
|---|---|---|
| × | símbolo de tiempos | 3 × 4 |
| · | punto | 3 · 4 |
| () | paréntesis | (3) (4) o 3 (4) de (3) 4 |
Productos y factores
En la expresión\(3 · 4\), los números enteros 3 y 4 se llaman los factores y\(3 · 4\) se llama el producto.
La clave para entender la multiplicación se sostiene en el siguiente enunciado.
La multiplicación equivale a la adición repetida.
Supongamos, por ejemplo, que nos gustaría evaluar el producto\(3 ·4\). Debido a que la multiplicación equivale a la adición repetida,\(3 · 4\) equivale a sumar tres cuatro patas. Es decir,
\[ 3 \cdot 4=\underbrace{4+4+4}_{\text { three fours }} \nonumber\]
Por lo tanto,\(3 · 4 = 12\). Se puede visualizar el producto\(3 · 4\) como la suma de tres cuatros en una recta numérica, como se muestra en la Figura 1.6.

Al igual que la suma, el orden de los factores no importa.
\[ 4 \cdot 3=\underbrace{3+3+3+3}_{\text { four threes }} \nonumber\]
Por lo tanto,\(4 · 3 = 12\). Considere la visualización de\(4 · 3\) en la Figura 1.7.

La evidencia de la Figura 1.6 y la Figura 1.7 nos muestran que la multiplicación es conmutativa. Es decir,
\[3 · 4=4 · 3 \nonumber\]
Propiedad conmutativa de la multiplicación
Si a y b son números enteros, entonces
\[a · b = b · a. \nonumber\]
La Identidad Multiplicativa
En la Figura 1.8 (a), nótese que cinco unos equivale a 5; es decir,\(5 · 1 = 5\). Por otra parte, en la Figura 1.8 (b), vemos que uno cinco equivale a cinco; es decir, 1 · 5 = 5.
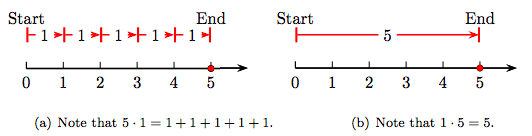
Debido a que multiplicar un número entero por 1 es igual a ese número idéntico, el número entero 1 se llama la identidad multiplicativa.
La propiedad de identidad multiplicativa
Si\(a\) hay algún número entero, entonces
a · 1 = a y 1 · a = a.
Multiplicación por Cero
Porque\(3 · 4 = 4 + 4 + 4\), podemos decir que el producto\(3 · 4\) representa “3 juegos de 4”, como se representa en la Figura 1.9, donde tres grupos de cuatro cajas están envueltos cada uno en un óvalo.
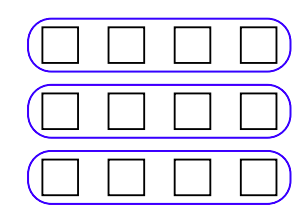
Por lo tanto,\(0 · 4\) significaría cero conjuntos de cuatro. Por supuesto, cero conjuntos de cuatro es cero.
Multiplicación por Cero.
Si a representa cualquier número entero, entonces
\(a · 0 = 0\)y\(0 · a = 0\).
La propiedad asociativa de la multiplicación
Al igual que la suma, la multiplicación de números enteros es asociativa. En efecto,
\[\begin{align*} 2 · (3 · 4) &= 2 · 12 \\[4pt] &= 24 \end{align*}\]
y
\[\begin{align*} (2 · 3) · 4 &=6 · 4 \\[4pt] &= 24. \end{align*}\]
La propiedad asociativa de la multiplicación.
Si a, b y c son números enteros, entonces
\[a · (b · c)=(a · b) · c. \nonumber\]
Multiplicar números enteros más grandes
Al igual que la suma y resta de números enteros grandes, también necesitaremos multiplicar números enteros grandes. De nuevo, esperamos que el algoritmo sea familiar a partir de cursos anteriores.
Ejemplo 1
Simplificar:\(35 · 127\).
Solución
Alinee los números verticalmente. El orden de multiplicación no importa, pero pondremos el mayor de los dos números encima del número menor. El primer paso es multiplicar 5 por 127. Nuevamente, procedemos de derecha a izquierda. Entonces, 5 veces 7 es 35. Escribimos el 5, luego llevamos el 3 a la columna de decenas. Siguiente, 5 veces 2 es 10. Suma el dígito de acarreo 3 para obtener 13. Escribe el 3 y lleva el 1 a la columna de cientos. Por último, 5 veces 1 es 5. Suma el dígito de acarreo para obtener 6.
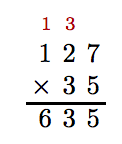
El siguiente paso es multiplicar 3 por 127. No obstante, debido a que 3 está en el lugar de las decenas, su valor es 30, por lo que en realidad multiplicamos 30 por 126. Esto es lo mismo que multiplicar 127 por 3 y colocar un 0 al final del resultado.
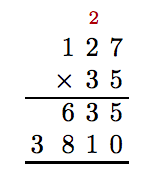
Después de sumar el 0, 3 veces 7 es 21. Escribimos el 1 y llevamos el 2 arriba del 2 en la columna de decenas. Entonces, 3 veces 2 es 6. Suma el dígito de acarreo 2 para obtener 8. Por último, 3 veces 1 es 1.
Todo lo que queda por hacer es sumar los resultados.
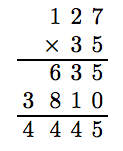
Así, 35 · 127 = 4, 445.
Formato Alternativo
No está de más omitir el cero final en el segundo paso de la multiplicación, donde multiplicamos 3 por 127. El resultado se vería así:
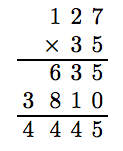
En este formato, se entiende el cero, por lo que no es necesario tenerlo físicamente presente. La idea es que con cada multiplicación por un nuevo dígito, sanguemos al producto un espacio desde la derecha.
Ejercicio
Simplificar: 56 · 335
- Contestar
-
18,760
División de Números Enteros
Pasamos ahora al tema de la división de números enteros. Primero introducimos los diversos símbolos utilizados para indicar la división de números enteros.
Símbolos matemáticos que indican división
| Símbolo | Ejemplo | |
|---|---|---|
| ÷ | símbolo de división | 12 ÷ 4 |
| - | barra de fracción | \(\frac{12}{4}\) |
| \(\longdiv{-}\) | barra de división | \(4 \longdiv{12}\) |
Tenga en cuenta que cada uno de los siguientes dice lo mismo; es decir, “12 dividido por 4 es 3”.
\(12 \div 4=3 \quad \text { or } \quad \frac{12}{4}=3 \quad \text { or } \quad 4 \sqrt{12}\)
Cocientes, Dividendos y Divisores
En el comunicado
\(\frac{3}{4 ) 12}\)
el número entero 12 se llama dividendo, el número entero 4 se llama divisor, y el número entero 3 se llama cociente. Tenga en cuenta que esta notación de barras de división es equivalente a
\(12 \div 4=3 \quad \text { and } \quad \frac{12}{4}=3.\)
La expresión a/b significa “a dividido por b”, pero este constructo también se llama fracción.
Definición: Fracción
La expresión
\( \frac{a}{b}\)
se llama fracción. El número\(a\) en la parte superior se llama el numerador de la fracción; el número\(b\) en la parte inferior se llama denominador de la fracción.
La clave para entender la división de números enteros está contenida en la siguiente declaración.
La división equivale a la resta repetida.
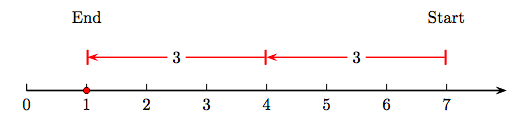
Supongamos por ejemplo, que nos gustaría dividir el número entero 12 por el número entero 4. Esto equivale a hacer la pregunta “¿cuántos cuatro patas podemos restar de 12?” Esto se puede visualizar en un diagrama de líneas numéricos, como el de la Figura 1.10.

En la Figura 1.10, nótese que nosotros si restamos tres cuatro patas de doce, el resultado es cero. En símbolos,
\( 12-\underbrace{4-4-4}_{\text { three fours }}=0.\)
De manera equivalente, también podemos preguntar “Cuántos grupos de cuatro hay en 12”, y organizar nuestro trabajo como se muestra en la Figura 1.11, donde podemos ver que en una matriz de doce objetos, podemos rodear tres grupos de cuatro; es decir, 12 ÷ 4 = 3.
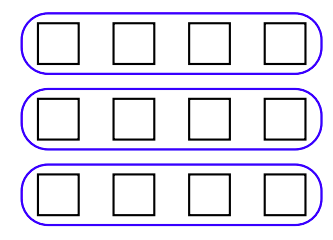
En la Figura 1.10 y la Figura 1.11, nótese que la división (resta repetida) no deja resto. Este no es siempre el caso.
Ejemplo 2.
Divide 7 por 3.
Solución
En la Figura 1.12, podemos ver que podemos restar dos tres de siete, dejando un resto de uno.
Alternativamente, en una matriz de siete objetos, podemos rodear dos grupos de tres, dejando un resto de uno.
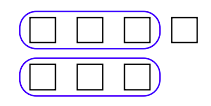
Tanto la Figura 1.12 como la Figura1.13 muestran que hay dos grupos de tres en siete, con uno sobrante. Decimos “Siete dividido por tres es dos, con un resto de uno.
Ejercicio
Utilice tanto el enfoque de la línea numérica como el enfoque de matriz de cajas para dividir 12 por 5.
La división no es conmutativa
Al dividir números enteros, el orden importa. Por ejemplo
12 ÷ 4 = 3,
pero 4 ÷ 12 no es ni siquiera un número entero. Así, si a y b son números enteros, entonces a ÷ b no tiene que ser lo mismo que b ÷ a.
La división no es asociativa
Cuando divides tres números, el orden en el que se agrupan suele afectar la respuesta. Por ejemplo,
(48 ÷ 8) ÷ 2=6 ÷ 2
= 3,
pero
48 ÷ (8 ÷ 2) = 48 ÷ 4
= 12.
Así, si a, b y c son números enteros, (a ÷ b) ÷ c no tiene que ser lo mismo que a ÷ (b ÷ c).
División por Cero no está definida
Supongamos que se nos pide dividir seis por cero; es decir, se nos pide calcular 6 ÷ 0. En la Figura 1.14, tenemos una matriz de seis objetos.
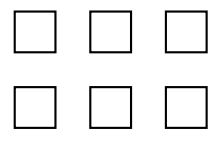
Ahora bien, para dividir seis por cero, debemos responder a la pregunta “¿Cuántos grupos de cero podemos rodear en la Figura 1.14?” Algún pensamiento proporcionará la respuesta: ¡Esta es una solicitud sin sentido! No tiene absolutamente ningún sentido preguntar cuántos grupos de cero pueden ser rodeados en la matriz de seis objetos en la Figura 1.14.
División por Cero
La división por cero no está definida. Cada una de las expresiones
\(6 \div 0 \quad \text { and } \quad \frac{6}{0} \quad \text { and } \quad 0 ) \overline{6}\)
está indefinido.
Por otro lado, tiene sentido preguntar “¿Qué es cero dividido por seis?” Si creamos una matriz de cero objetos, entonces preguntamos cuántos grupos de seis podemos rodear, la respuesta es “cero grupos de seis”. Es decir, cero dividido por seis es cero.
\( 0 \div 6=0 \quad \text { and } \quad \frac{0}{6}=0 \quad \text { and } \quad 6 \frac{0}{0}\)
Dividir números enteros más grandes
Ahora proporcionaremos una revisión rápida de la división de números enteros más grandes, usando un algoritmo que comúnmente se llama división larga. Esto no pretende ser una discusión a fondo, sino superficial. Contamos con el hecho de que nuestros lectores han encontrado este algoritmo en cursos anteriores y están familiarizados con el proceso.
Ejemplo 3
Simplificar: 575/23.
Solución
Comenzamos por estimar cuántas veces 23 se dividirán en 57, adivinando 1. Ponemos el 1 en el cociente por encima del 7, multiplicamos 1 por 23, colocamos la respuesta por debajo de 57, luego restamos.
\(\begin{array}{c}{23 ) \frac{1}{575}} \\ {\frac{23}{34}}\end{array}\)
Debido a que el resto es mayor que el divisor, nuestra estimación es demasiado pequeña. Lo intentamos de nuevo con una estimación de 2.
\(\begin{array}{r}{2} \\ {2 3 \longdiv { 5 7 5 }} \\ {\frac{46}{11}}\end{array}\)
Ese es el algoritmo. Dividir, multiplicar, luego restar. Usted podrá continuar sólo cuando el resto sea menor que el divisor.
Para continuar, bajar el 5, estimar que 115 dividido por 23 es 5, luego multiplicar 5 veces el divisor y restar.
\(\begin{array}{c}{25} \\ {2 3 \longdiv { 5 7 5 }} \\ {\frac{46}{115}} \\ {\frac{115}{0}}\end{array}\)
Debido a que el resto es cero, 575/23 = 25.
Ejercicio
Divide 980/35
- Contestar
-
28
Aplicación — Conteo de Matrices Rectangulares
Considere la matriz rectangular de estrellas en la Figura 1.15. Para contar el número de estrellas en la matriz, podríamos usar la fuerza bruta, contando cada estrella en la matriz una a la vez, para un total de 20 estrellas. No obstante, como tenemos cuatro filas de cinco estrellas cada una, es mucho más rápido de multiplicar: 4 · 5 = 20 estrellas.

Aplicación — Área
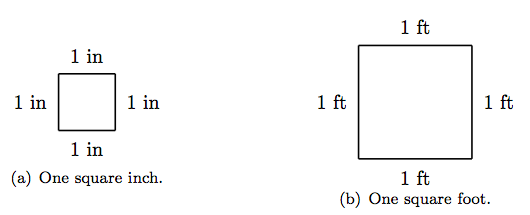
En la Figura 1.16 (a), se muestra una pulgada cuadrada (1 en 2), un cuadrado con una pulgada en cada lado. En la Figura 1.16 (b), en la foto se muestra un pie cuadrado (1 pie 2), un cuadrado con un pie a cada lado. Ambas plazas son medidas de área. Ahora, considere el rectángulo que se muestra en la Figura 1.17. La longitud de este rectángulo es de cuatro pulgadas (4 pulgadas) y el ancho es de tres pulgadas (3 pulgadas).
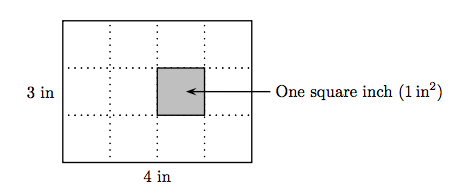
Para encontrar el área de la figura, podemos contar las unidades individuales de área que conforman el área del rectángulo, doce pulgadas cuadradas (12 en 2) en total. Sin embargo, como hicimos al contar las estrellas en la matriz en la Figura 1.15, es mucho más rápido notar que tenemos tres filas de cuatro pulgadas cuadradas. De ahí que sea mucho más rápido multiplicar el número de cuadrados en cada fila por el número de cuadrados en cada columna: 4·3 = 12 pulgadas cuadradas.
El argumento presentado anteriormente lleva a la siguiente regla para encontrar el área de un rectángulo.
Área de un Rectángulo
Deje que L y W representen el largo y ancho de un rectángulo, respectivamente.
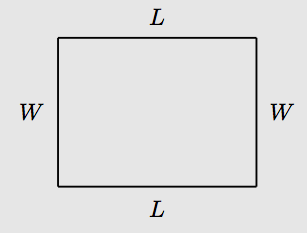
Para encontrar el área del rectángulo, calcule el producto del largo y ancho. Es decir, si A representa el área del rectángulo, entonces el área del rectángulo viene dada por la fórmula
A = LW.
Ejemplo 4
Un rectángulo tiene un ancho de 5 pies y un largo de 12 pies. Encuentra el área del rectángulo.
Solución
Sustituya L = 12 pies y W = 5 pies en la fórmula de área.
A = LW
= (12 pies) (5 pies)
= 60 ft 2
De ahí que el área del rectángulo sea de 60 pies cuadrados.
Ejercicio
Un rectángulo tiene ancho 17 pulgadas y largo 33 pulgadas. Encuentra el área del rectángulo.
- Contestar
-
561 pulgadas cuadradas
Ejercicios
En los Ejercicios 1-4 se utilizan diagramas de líneas numéricas como se muestra en la Figura 1.6 para representar la multiplicación.
1. 2 · 4.
2. 3 · 4.
3. 4 · 2.
4. 4 · 3.
En los Ejercicios 5-16, declarar la propiedad de multiplicación representada por la identidad dada.
5. 9 · 8=8 · 9
6. 5 · 8=8 · 5
7. 8 · (5 · 6) = (8 · 5) · 6
8. 4 · (6 · 5) = (4 · 6) · 5
9. 6 · 2=2 · 6
10. 8 · 7=7 · 8
11. 3 · (5 · 9) = (3 · 5) · 9
12. 8 · (6 · 4) = (8 · 6) · 4
13. 21 · 1 = 21
14. 39 · 1 = 39
15. 13 · 1 = 13
16. 44 · 1 = 44
En los Ejercicios 17-28, multiplique los números dados.
17. 78 · 3
18. 58 · 7
19. 907 · 6
20. 434 · 80
21. 128 · 30
22. 454 · 90
23. 799 · 60
24. 907 · 20
25. 14 · 70
26. 94 · 90
27. 34 · 90
28. 87 · 20
En los Ejercicios 29-40, multiplique los números dados.
29. 237 · 54
30. 893 · 94
31. 691 · 12
32. 823 · 77
33. 955 · 89
34. 714 · 41
35. 266 · 61
36. 366 · 31
37. 365 · 73
38. 291 · 47
39. 955 · 57
40. 199 · 33
41. Contar el número de objetos en la matriz.

42. Contar el número de objetos en la matriz.

43. Contar el número de objetos en la matriz.

44. Contar el número de objetos en la matriz.

En Ejercicios 45-48, encuentra el área del rectángulo que tiene la longitud y anchura dadas.
45. L = 50 in, W = 25 in
46. L = 48 pulgadas, W = 24 pulgadas
47. L = 47 pulgadas, W = 13 pulgadas
48. L = 19 pulgadas, W = 10 pulgadas
En los Ejercicios 49-52, encuentra el perímetro del rectángulo que tiene la longitud y anchura dadas.
49. L = 25 in, W = 16 in
50. L = 34 pulgadas, W = 18 pulgadas
51. L = 30 pulgadas, W = 28 pulgadas
52. L = 41 pulgadas, W = 25 pulgadas
53. Un juego de cuentas cuesta 50 centavos por docena. ¿Cuál es el costo (en dólares) de 19 docenas de juegos de cuentas?
54. Un juego de cuentas cuesta 60 centavos por docena. ¿Cuál es el costo (en dólares) de 7 docenas de juegos de cuentas?
55. Si un tutor de matemáticas trabajó 47 horas y se le pagaba 15 dólares cada hora, ¿cuánto dinero habría ganado?
56. Si un tutor de matemáticas trabajó 46 horas y se le pagaba $11 cada hora, ¿cuánto dinero habría ganado?
57. Hay 12 huevos en una docena, y 12 docenas en una bruta. ¿Cuántos huevos hay en un envío de 24 brutos?
58. Hay 12 huevos en una docena, y 12 docenas en una bruta. ¿Cuántos huevos hay en un envío de 11 brutos?
59. Si los ladrillos pesan 4 kilogramos cada uno, ¿cuál es el peso (en kilogramos) de 5000 ladrillos?
60. Si los ladrillos pesan 4 libras cada uno, ¿cuál es el peso (en libras) de 2000 ladrillos?
En los Ejercicios 61-68, ¿cuál de las siguientes cuatro expresiones difiere de las tres restantes?
61. \(\frac{30}{5}\), 30 ÷ 5,\(5 \longdiv { 3 0 }\), 5 ÷ 30
62. \(\frac{12}{2}\), 12 ÷ 2,\(2 \longiv{12}\), 2 ÷ 12
63. \(\frac{8}{2}\), 8 ÷ 2,\(2 \longdiv{8}\),\(8 \longdiv{2}\)
64. \(\frac{8}{4}\), 8 ÷ 4,\(4 \longdiv { 8 }\),\(8 \longdiv { 4 }\)
65. \(2 \longdiv { 14 }\),\(14 \longdiv { 2 }\)\(\frac{14}{2}\), 14 ÷ 2
66. \(9 \longdiv { 54 }\),\(54 \longdiv { 9 }\)\(\frac{54}{9}\), 54 ÷ 9
67. \(3 \longdiv { 24 }\), 3 ÷ 24,\(\frac{24}{3}\), 24 ÷ 3
68. \(3 \longdiv { 15 }\), 3 ÷ 15,\(\frac{15}{3}\), 15 ÷ 3
En los Ejercicios 69-82, simplificar la expresión dada. Si la respuesta no existe o es indefinida, escribe “undefined”.
69. 0 ÷ 11
70. 0 ÷ 5
71. 17 ÷ 0
72. 24 ÷ 0
73. 10 · 0
74. 20 · 0
75. \(\frac{7}{0}\)
76. \(\frac{23}{0}\)
77. \(16 \longdiv { 0 }\)
78. \(25 \longdiv { 0 }\)
79. \(\frac{0}{24}\)
80. \(\frac{0}{22}\)
81. \(0 \longdiv { 0 }\)
82. 0 ÷ 0
En Ejercicios 83-94, divide los números dados.
83. \(\frac{2816}{44}\)
84. \(\frac{1998}{37}\)
85. \(\frac{2241}{83}\)
86. \(\frac{2716}{97}\)
87. \(\frac{3212}{73}\)
88. \(\frac{1326}{17}\)
89. \(\frac{8722}{98}\)
90. \(\frac{1547}{91}\)
91. \(\frac{1440}{96}\)
92. \(\frac{2079}{27}\)
93. \(\frac{8075}{85}\)
94. \(\frac{1587}{23}\)
En Ejercicios 95-106, divida los números dados.
95. \(\frac{17756}{92}\)
96. \(\frac{46904}{82}\)
97. \(\frac{11951}{19}\)
98. \(\frac{22304}{41}\)
99. \(\frac{18048}{32}\)
100. \(\frac{59986}{89}\)
101. \(\frac{29047}{31}\)
102. \(\frac{33264}{86}\)
103. \(\frac{22578}{53}\)
104. \(\frac{18952}{46}\)
105. \(\frac{12894}{14}\)
106. \(\frac{18830}{35}\)
107. Una acera de concreto se coloca en bloques cuadrados que miden 6 pies a cada lado. ¿Cuántas cuadras habrá en una caminata de 132 pies de largo?
108. Una acera de concreto se coloca en bloques cuadrados que miden 5 pies a cada lado. ¿Cuántas cuadras habrá en una caminata de 180 pies de largo?
109. Un barco a la isla puede llevar 5 personas. ¿Cuántos viajes tendrá que realizar el barco para transportar a 38 personas a la isla? (Pista: Redondee su respuesta.)
110. Un barco a la isla puede llevar 4 personas. ¿Cuántos viajes tendrá que realizar el barco para transportar a 46 personas a la isla? (Pista: Redondee su respuesta.)
111. Si las luces de la calle se colocan a lo sumo 145 pies de distancia, ¿cuántas farolas se necesitarán para una calle de 4 millas de largo, suponiendo que haya luces en cada extremo de la calle? (Nota: 1 milla = 5280 pies.)
112. Si las luces de la calle se colocan como máximo a 70 pies de distancia, ¿cuántas farolas se necesitarán para una calle de 3 millas de largo, suponiendo que haya luces en cada extremo de la calle? (Nota: 1 milla = 5280 pies.)
113. Una acera de concreto se coloca en bloques cuadrados que miden 4 pies a cada lado. ¿Cuántas cuadras habrá en una caminata de 292 pies de largo?
114. Una acera de concreto se coloca en bloques cuadrados que miden 5 pies a cada lado. ¿Cuántas cuadras habrá en una caminata de 445 pies de largo?
115. Un barco a la isla puede llevar 3 personas. ¿Cuántos viajes tendrá que realizar el barco para transportar a 32 personas a la isla? (Pista: Redondee su respuesta.)
116. Un barco a la isla puede llevar 4 personas. ¿Cuántos viajes tendrá que realizar el barco para transportar a 37 personas a la isla? (Pista: Redondee su respuesta.)
117. Si las luces de la calle se colocan a lo sumo 105 pies de distancia, ¿cuántas farolas se necesitarán para una calle de 2 millas de largo, suponiendo que haya luces en cada extremo de la calle? (Nota: 1 milla = 5280 pies.)
118. Si las luces de la calle se colocan a lo sumo 105 pies de distancia, ¿cuántas farolas se necesitarán para una calle de 3 millas de largo, suponiendo que haya luces en cada extremo de la calle? (Nota: 1 milla = 5280 pies.)
119. Redacción de artículos. Eli escribe un promedio de 4 artículos al día, cinco días a la semana, para apoyar las ventas de productos. ¿Cuántos artículos escribe Eli en una semana?
120. Ametralladora. Una ametralladora antiaérea calibre 0.50 puede disparar 800 proyectiles cada minuto. ¿Cuántos proyectiles podrían disparar en tres minutos? Tiempos de Prensa Asociados Estándar 4/15/09
121. Vueltas. La piscina de CalCourts tiene 25 yardas de largo. Si una vuelta está arriba y atrás otra vez, ¿cuántas yardas ha nadado Wendell haciendo 27 vueltas?
122. Vatiaje del refrigerador. Un refrigerador convencional funcionará aproximadamente 12 horas cada día puede usar 150 Watts de potencia cada hora. ¿Cuántos Watts de potencia utilizará un refrigerador a lo largo del día?
123. Heno de caballos. Un caballo adulto debe comer un mínimo de 12 libras de heno cada día y puede comer mucho más dependiendo de su peso. ¿Cuántas libras mínimo comería un caballo a lo largo de un año?
124. Costos universitarios. Después de un alza de 662 dólares en las tarifas, los residentes de Califormia que quieran asistir a la Universidad de California como licenciatura deben esperar pagar $8,700 en el próximo año académico 2009- 2010. Si el costo siguiera siendo el mismo durante los próximos años, ¿cuánto debería esperar pagar un estudiante por un programa de grado de cuatro años en una escuela de la UC?
125. Costos de no residentes. Los estudiantes universitarios no residentes que quieran asistir a una universidad de la Universidad de California deben esperar pagar alrededor de $22,000 por el próximo año académico. Suponiendo que los costos sigan siendo los mismos, ¿qué puede costar un título de cuatro años
126. Impuesto estudiantil. El mayer de Providence, Rhode Island quiere gravar a sus 25 mil estudiantes de la Universidad Brown $150 cada uno para contribuir a recibos de impuestos diciendo que los estudiantes deben pagar por los recursos que utilizan al igual que los residentes de la ciudad. ¿Cuántos dólares generaría el mayer?
127. Nuevo iceberg. Un nuevo iceberg, raspado de un glaciar después de una colisión con otro iceberg, mide aproximadamente 48 millas de largo y 28 millas de ancho. ¿Cuál es el área aproximada del nuevo iceberg? Prensas asociadas estándar 02/27/10 2 Enormes icebergs se sueltan frente a la costa de la Antártida.
128. Paneles solares. Uno de los paneles solares de la Estación Espacial Internacional tiene 34 metros de largo y 11 metros de ancho. Si hay ocho de estos, ¿cuál es el área total para la recolección solar?
129. Acera. Una acera de concreto debe tener 80 pies de largo y 4 pies de ancho. ¿Cuánto costará tender la acera a 8 dólares por pie cuadrado?
130. Pacas de heno. Una paca promedio de heno pesa alrededor de 60 libras. Si un caballo come 12 libras de heno al día, ¿cuántos días una bala alimentará a un caballo?
131. Manchas solares. Las manchas solares, donde el campo magnético del sol es mucho mayor, suelen ocurrir en parejas. Si el recuento total de manchas solares es de 72, ¿cuántos pares de manchas solares hay?
RESPUESTAS
1. \(2 \cdot 4=\underbrace{4+4}_{2 \text { times }}=8\)
3. \(4 \cdot 2=\underbrace{2+2+2+2}_{4 \text { times }}=8\)
5. Propiedad conmutativa de la multiplicación
7. Propiedad asociativa de la multiplicación
9. Propiedad conmutativa de la multiplicación
11. Propiedad asociativa de la multiplicación
13. Propiedad de identidad multiplicativa
15. Propiedad de identidad multiplicativa
17. 234
19. 5442
21. 3840
23. 47940
25. 980
27. 3060
29. 12798
31. 8292
33. 84995
35. 16226
37. 26645
39. 54435
41. 64
43. 56
45. 1250 en 2
47. 611 en 2
49. 82 in
51. 116 en
53. 9.50
55. 705
57. 3456
59. 20000
61. 5 ÷ 30
63. \(8 \sqrt{2}\)
65. \(14 \sqrt{2}\)
67. 3 ÷ 24
69. 0
71. Sin definir
73. 0
75. Sin definir
77. 0
79. 0
81. Sin definir
83. 64
85. 27
87. 44
89. 89
91. 15
93. 95
95. 193
97. 629
99. 564
101. 937
103. 426
105. 921
107. 22
109. 8
111. 147
113. 73
115. 11
117. 102
119. 20 artículos
121. 1350 yardas
123. 4380 libras de heno
125. $88,000
127. 1344 mi 2
129. $2,560
131. 36


