1.4: Factorización Prime

Última actualización
Guardar como PDF

Page ID: 113397

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En el enunciado 3 · 4 = 12, el número 12 se llama el producto, mientras que 3 y 4 se denominan factores.

Ejemplo 1

Encuentra todos los factores número entero de 18.

Solución

Necesitamos encontrar todos los pares de números enteros cuyo producto sea igual a 18. Me vienen a la mente los siguientes pares.

1 · 18 = 18 y 2 · 9 = 18 y 3 · 6 = 18.

De ahí que los factores de 18 son (en orden) 1, 2, 3, 6, 9 y 18.

Ejercicio

Encuentra todos los factores número entero de 21.

Contestar: 1, 3, 7 y 21

Divisibilidad

En el Ejemplo 1, vimos 3 · 6 = 18, haciendo 3 y 6 factores de 18. Debido a que la división es la inversa de la multiplicación, es decir, la división por un número deshace la multiplicación de ese número, esto proporciona inmediatamente

18 ÷ 6 = 3 y 18 ÷ 3=6.

Es decir, 18 es divisible por 3 y 18 es divisible por 6. Cuando decimos que 18 es divisible por 3, queremos decir que cuando 18 se divide por 3, hay un resto cero.

Divisible

Que a y b sean números enteros. Entonces a es divisible por b si y solo si el resto es cero cuando a se divide por b. En este caso, decimos que “b es un divisor de a”.

Ejemplo 2

Encuentra todos los divisores de número entero de 18.

Solución

En el Ejemplo 1, vimos que 3 · 6 = 18. Por lo tanto, 18 es divisible tanto por 3 como por 6 (18 ÷ 3 = 6 y 18 ÷ 6 = 3). De ahí que cuando 18 se divide por 3 o 6, el resto es cero. Por lo tanto, 3 y 6 son divisores de 18. Tomando nota de los demás productos del Ejemplo 1, la lista completa de divisores de 18 es 1, 2, 3, 6, 9 y 18.

Ejercicio

Encuentra todos los divisores de números enteros de 21.

Contestar: 1, 3, 7 y 21.

El Ejemplo 1 y el Ejemplo 2 muestran que cuando se trabaja con números enteros, las palabras factor y divisor son intercambiables.

Factores y divisores

Si c = a · b, entonces a y b se denominan factores de c. Tanto a como b también se denominan divisores de c.

Pruebas de Divisibilidad

Hay una serie de pruebas de divisibilidad muy útiles.

Divisible por 2. Si un número entero termina en 0, 2, 4, 6 u 8, entonces el número se llama número par y es divisible por 2. Ejemplos de números pares son 238 y 1,246 (238 ÷ 2 = 119 y 1, 246 ÷ 2 = 623). Un número que no es par se llama número impar. Ejemplos de números impares son 113 y 2,339.

Divisible por 3. Si la suma de los dígitos de un número entero es divisible por 3, entonces el número en sí es divisible por 3. Un ejemplo es 141. La suma de los dígitos es 1 + 4 + 1 = 6, que es divisible por 3. Por lo tanto, 141 también es divisible por 3 (141 ÷ 3 = 47).

Divisible por 4. Si el número representado por los dos últimos dígitos de un número entero es divisible por 4, entonces el número en sí es divisible por 4. Un ejemplo es 11,524. Los dos últimos dígitos representan 24, que es divisible por 4 (24 ÷ 4 = 6). Por lo tanto, 11.524 es divisible por 4 (11, 524 ÷ 4=2, 881).

Divisible por 5. Si un número entero termina en un cero o un 5, entonces el número es divisible por 5. Ejemplos son 715 y 120 (715÷5 = 143 y 120÷5 = 24).

Divisible por 6. Si un número entero es divisible por 2 y por 3, entonces es divisible por 6. Un ejemplo es 738. Primero, 738 es par y divisible por 2. Segundo, 7+3+8=18, que es divisible por 3. De ahí que 738 es divisible por 3. Debido a que 738 es divisible por 2 y 3, es divisible por 6 (738 ÷ 6 = 123).

Divisible por 8. Si el número representado por los tres últimos dígitos de un número entero es divisible por 8, entonces el número en sí es divisible por 8. Un ejemplo es 73,024. Los últimos tres dígitos representan el número 24, que es divisible por 8 (24÷8 = 3). Así, 73.024 también es divisible por 8 (73, 024÷8 = 9, 128).

Divisible por 9. Si la suma de los dígitos de un número entero es divisible por 9, entonces el número en sí es divisible por 9. Un ejemplo es 117. La suma de los dígitos es 1 + 1 + 7 = 9, que es divisible por 9. De ahí que 117 es divisible por 9 (117 ÷ 9 = 13).

Números primos

Comenzamos con la definición de un número primo.

Número Primo

Un número entero (distinto de 1) es un número primo si sus únicos factores (divisores) son 1 y en sí mismo. De manera equivalente, un número es primo si y sólo si tiene exactamente dos factores (divisores).

Ejemplo 3

¿Cuáles de los números enteros 12, 13, 21 y 37 son números primos?

Solución

Los divisores de 12 son 1, 2, 3, 4, 6 y 12. De ahí que 12 no sea un número primo.
Los divisores de 13 son 1 y 13. Debido a que sus únicos divisores son 1 y en sí mismo, 13 es un número primo.
Los divisores de 21 son 1, 3, 7 y 21. De ahí que 21 no es un número primo.
Los divisores de 37 son 1 y 37. Debido a que sus únicos divisores son 1 y en sí mismo, 37 es un número primo.

Ejercicio

¿Cuáles de los números enteros 15, 23, 51 y 59 son números primos?

Contestar: 23 y 59

Ejemplo 4

Enumere todos los números primos menores a 20.

Solución

Los números primos menores a 20 son 2, 3, 5, 7, 11, 13, 17 y 19.

¡Lo intentas!

Enumere todos los números primos menores a 100.

Números compuestos

Si un número entero no es un número primo, entonces se llama número compuesto.

Ejemplo 5

¿Es el número entero 1.179 primo o compuesto?

Solución

Obsérvese que 1 + 1 + 7 + 9 = 18, que es divisible tanto por 3 como por 9. De ahí que 3 y 9 sean ambos divisores de 1,179. Por lo tanto, 1,179 es un número compuesto.

Ejercicio

¿Es el número entero 2.571 primo o compuesto?

Contestar: Composite

Árboles de factor

Ahora aprenderemos a expresar un número compuesto como un producto único de números primos. El dispositivo más popular para lograr este objetivo es el árbol de factores.

Ejemplo 6

Express 24 como producto de factores primos.

Solución

Utilizamos un árbol factorial para descomponer 24 en un producto de primos.

$Screen Shot 2019-08-07 a las 8.00.41 PM.png$

En cada nivel del árbol, divida el número actual en un producto de dos factores. El proceso se completa cuando todas las “hojas en círculo” en la parte inferior del árbol son números primos. Arreglando los factores en las “hojas en círculo” en orden,

24 = 2 · 2 · 2 · 3.

La respuesta final no depende de las elecciones de productos que se hagan en cada nivel del árbol. Aquí hay otro enfoque.

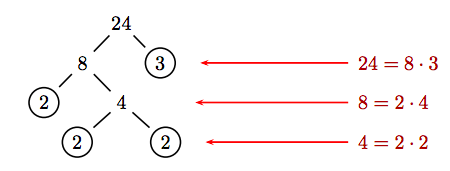
$Screen Shot 2019-08-07 a las 8.00.48 PM.png$

La respuesta final se encuentra al incluir todos los factores de las “hojas en círculo” al final de cada rama del árbol, lo que arroja el mismo resultado, a saber 24 = 2 · 2 · 2 · 3.

Enfoque Alternativo

Algunos favorecen dividir repetidamente por 2 hasta que el resultado ya no sea divisible por 2. Entonces intenta dividir repetidamente por el siguiente primo hasta que el resultado ya no sea divisible por ese primo. El proceso termina cuando el último cociente resultante es igual al número 1.

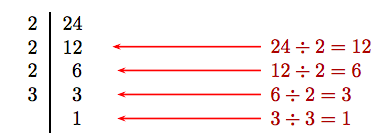
$Screen Shot 2019-08-07 a las 8.00.56 PM.png$

La primera columna revela la factorización prima; es decir, 24 = 2 · 2 · 2 · 3.

Ejercicio

Express 36 como producto de factores primos.

Contestar: 2 · 2 · 3 · 3.

El hecho de que el enfoque alternativo en el Ejemplo 6 arrojó el mismo resultado es significativo.

Teorema de Factorización Único

Cada número entero puede ser factorizado de manera única como un producto de primos.

Este resultado garantiza que si los factores primos se ordenan de menor a mayor, todos obtendrán el mismo resultado al dividir un número en un producto de factores primos.

Exponentes

Comenzamos con la definición de una expresión exponencial.

Exponentes

La expresión a ^m se define como

$ a^{m}=\underbrace{a \cdot a \cdot \ldots \cdot a}_{m \text { times }}$

El número a se llama la base de la expresión exponencial y el número m se llama exponente. El exponente m nos dice repetir la base a como factor m veces.

Ejemplo 7

Evaluar 2 ⁵, 2 ³, y 5 ².

Solución

En el caso de 2 ⁵, tenemos

2 ⁵ = 2 · 2 · 2 · 2 · 2

= 32.

En el caso de ^{3 3}, tenemos

3 ³ = 3 · 3 · 3

= 27.

En el caso de 5 ², tenemos

5 ² = 5 · 5

= 25.

Ejercicio

Evaluar: 3 ⁵.

Contestar: 243.

Ejemplo 8

Exprese la solución al Ejemplo 6 en forma compacta usando exponentes.

Solución

En el Ejemplo 6, se determinó la factorización prima de 24.

24 = 2 · 2 · 2 · 3

Porque 2 · 2 · 2=23, podemos escribir esto de manera más compacta.

24 = 2 ³ · 3

Ejercicio

Factor primo 54.

Contestar: 2 · 3 · 3 · 3

Ejemplo 9

Evaluar la expresión 2 ³ · 3 ² · 5 ².

Solución

Primero eleva cada factor al exponente dado, luego realiza la multiplicación en orden (de izquierda a derecha).

2 ³ · 3 ² · 5 ² = 8 · 9 · 25

= 72 · 25

= 1800

Ejercicio

Evaluar: ^{3 3} · 5 ².

Contestar: 675

Aplicación

Un cuadrado es un rectángulo con cuatro lados iguales.

Área de un cuadrado

Representemos la longitud de cada lado de un cuadrado.

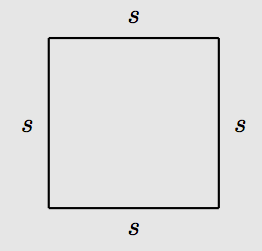
$Screen Shot 2019-08-07 at 8.08.27 PM.png$

Debido a que un cuadrado es también un rectángulo, podemos encontrar el área del cuadrado multiplicando su longitud y anchura. Sin embargo, en este caso, tanto la longitud como la anchura son iguales a s, por lo que A = (s) (s) = s ². Por lo tanto, la fórmula para el área de un cuadrado es

A = s ².

Ejemplo 10

El borde de un cuadrado es de 13 centímetros. Encuentra el área de un cuadrado.

Solución

Sustituir s = 13 cm en la fórmula de área.

A = s ²

= (13 cm) ²

= (13 cm) (13 cm)

= 169 cm ²

De ahí que el área del cuadrado sea de 169 cm ²; es decir, 169 centímetros cuadrados.

Ejercicio

El borde de una plaza es de 15 metros. Encuentra el área de un cuadrado.

Contestar: 225 metros cuadrados

Ejercicios

En Ejercicios 1-12, encuentra todos los divisores del número dado.

1. 30

2. 19

3. 83

4. 51

5. 91

6. 49

7. 75

8. 67

9. 64

10. 87

11. 14

12. 89

En Ejercicios 13-20, ¿cuál de los siguientes números no es divisible por 2?

13. 117, 120, 342, 230

14. 310, 157, 462, 160

15. 30, 22, 16, 13

16. 382, 570, 193, 196

17. 105, 206, 108, 306

18. 60, 26, 23, 42

19. 84, 34, 31, 58

20. 66, 122, 180, 63

En Ejercicios 21-28, ¿cuál de los siguientes números no es divisible por 3?

21. 561, 364, 846, 564

22. 711, 850, 633, 717

23. 186, 804, 315, 550

24. 783, 909, 504, 895

25. 789, 820, 414, 663

26. 325, 501, 945, 381

27. 600, 150, 330, 493

28. 396, 181, 351, 606

En Ejercicios 29-36, ¿cuál de los siguientes números no es divisible por 4?

29. 3797, 7648, 9944, 4048

30. 1012, 9928, 7177, 1592

31. 9336, 9701, 4184, 2460

32. 2716, 1685, 2260, 9788

33. 9816, 7517, 8332, 7408

34. 1788, 8157, 7368, 4900

35. 1916, 1244, 7312, 7033

36. 7740, 5844, 2545, 9368

En Ejercicios 37-44, ¿cuál de los siguientes números no es divisible por 5?

37. 8920, 4120, 5285, 9896

38. 3525, 7040, 2185, 2442

39. 8758, 3005, 8915, 3695

40. 3340, 1540, 2485, 2543

41. 2363, 5235, 4145, 4240

42. 9030, 8000, 5445, 1238

43. 1269, 5550, 4065, 5165

44. 7871, 9595, 3745, 4480

En Ejercicios 45-52, ¿cuál de los siguientes números no es divisible por 6?

45. 328, 372, 990, 528

46. 720, 288, 148, 966

47. 744, 174, 924, 538

48. 858, 964, 930, 330

49. 586, 234, 636, 474

50. 618, 372, 262, 558

51. 702, 168, 678, 658

52. 780, 336, 742, 312

En Ejercicios 53-60, ¿cuál de los siguientes números no es divisible por 8?

53. 1792, 8216, 2640, 5418

54. 2168, 2826, 1104, 2816

55. 8506, 3208, 9016, 2208

56. 2626, 5016, 1392, 1736

57. 4712, 3192, 2594, 7640

58. 9050, 9808, 8408, 7280

59. 9808, 1232, 7850, 7912

60. 3312, 1736, 9338, 3912

En Ejercicios 61-68, ¿cuál de los siguientes números no es divisible por 9?

61. 477, 297, 216, 991

62. 153, 981, 909, 919

63. 153, 234, 937, 675

64. 343, 756, 927, 891

65. 216, 783, 594, 928

66. 504, 279, 307, 432

67. 423, 801, 676, 936

68. 396, 684, 567, 388

En los Ejercicios 69-80, identifique el número dado como primo, compuesto, o ninguno.

69. 19

70. 95

71. 41

72. 88

73. 27

74. 61

75. 91

76. 72

77. 21

78. 65

79. 23

80. 36

En Ejercicios 81-98, encuentra la factorización prima del número natural.

81. 224

82. 320

83. 108

84. 96

85. 243

86. 324

87. 160

88. 252

89. 32

90. 128

91. 360

92. 72

93. 144

94. 64

95. 48

96. 200

97. 216

98. 392

En Ejercicios 99-110, computa el valor exacto de la expresión exponencial dada.

99. 5 ² · 4 ¹

100. 2 ³ · 4 ¹

101. 0 ¹

102. 1 ³

103. 3 ³ · 0 ²

104. 3 ³ · 2 ²

105. 4 ¹

106. 5 ²

107. 4 ³

108. 4 ²

109. 3 ³ · 1 ²

110. 5 ² · 2 ³

En Ejercicios 111-114, encuentra el área de la plaza con el lado dado.

111. 28 pulgadas

112. 31 pulgadas

113. 22 pulgadas

114. 13 pulgadas

Crea árboles de factores para cada número en Ejercicios 115-122. Escribe la factorización prima para cada número en forma compacta, usando exponentes.

115. 12

116. 18

117. 105

118. 70

119. 56

120. 56

121. 72

122. 270

123. Tamiz de Eratóstenes. Este ejercicio introduce el Tamiz de Eratóstenes, un antiguo algoritmo para encontrar los primos menores que un cierto número n, creado por primera vez por el matemático griego Eratóstenes. Considera la cuadrícula de números enteros del 2 al 100.

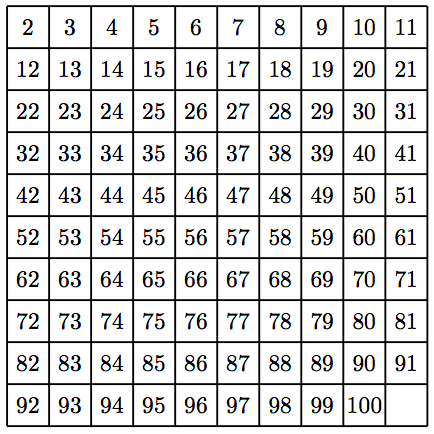
$Screen Shot 2019-08-07 at 8.53.48 PM.png$

Para encontrar los primos menores a 100, proceda de la siguiente manera.

i) Tachar todos los múltiplos de 2 (4, 6, 8, etc.)

ii) El siguiente número de la lista que no ha sido tachado es un número primo.

iii) Tachar de la lista todos los múltiplos del número que identificaste en el paso (ii).

iv) Repita los pasos (ii) y (iii) hasta que ya no pueda golpear más múltiplos.

v) Todos los números sin marcar de la lista son primos.

RESPUESTAS

1. 1, 2, 3, 5, 6, 10, 15, 30

3. 1, 83

5. 1, 7, 13, 91

7. 1, 3, 5, 15, 25, 75

9. 1, 2, 4, 8, 16, 32, 64

11. 1, 2, 7, 14

13. 117

15. 13

17. 105

19. 31

21. 364

23. 550

25. 820

27. 493

29. 3797

31. 9701

33. 7517

35. 7033

37. 9896

39. 8758

41. 2363

43. 1269

45. 328

47. 538

49. 586

51. 658

53. 5418

55. 8506

57. 2594

59. 7850

61. 991

63. 937

65. 928

67. 676

69. prime

71. prime

73. compuesto

75. compuesto

77. compuesto

79. primo

81. 2 · 2 · 2 · 2 · 7

83. 2 · 2 · 3 · 3 · 3

85. 3 · 3 · 3 · 3 · 3

87. 2 · 2 · 2 · 2 · 5

89. 2 · 2 · 2 · 2 · 2

91. 2 · 2 · 2 · 3 · 3 · 5

93. 2 · 2 · 2 · 2 · 3 · 3

95. 2 · 2 · 2 · 2 · 3

97. 2 · 2 · 2 · 3 · 3 · 3

99. 100

101. 0

103. 0

105. 4

107. 64

109. 27

111. 784 en ²

113. 484 en ²

115. 12 = 22 · 3

117. 105 = 3 · 5 · 7

119. 56 = 23 · 7

121. 72 = 23 · 32

123. Los números no tachados son primos: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Search

Text Color

Text Size

Margin Size

Font Type