8.3: Graficar ecuaciones lineales
- Page ID
- 113441
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Considera\(y = x + 1\) una ecuación en dos variables. Si sustituimos el par ordenado\((x, y) = (1, 2)\) en la ecuación\(y = x + 1\), es decir, si reemplazamos x por 1 e y con 2, obtenemos una declaración verdadera.
\[ \begin{aligned} y = x + 1 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 2=1+1 ~ & \textcolor{red}{ \text{ Substitute: 1 for } x \text{ and 2 for } y.} \\ 2=2 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Decimos que el par ordenado (1, 2) es una solución de la ecuación\(y = x + 1\).
Solución de una ecuación en dos variables
Si sustituir el par ordenado (x, y) =( a, b) en una ecuación (reemplazar x por a e y con b) produce una declaración verdadera, entonces el par ordenado (a, b) se llama solución de la ecuación y se dice que “satisface el ecuación.”
Ejemplo 1
¿Cuáles de los pares ordenados son soluciones de la ecuación\(y = 2x + 5\): (a) (−3, −2) o (b) (5, 15)?
Solución
Sustituir los puntos en la ecuación para determinar cuáles son las soluciones.
a) Para determinar si (−3, −2) es una solución de\(y = 2x + 5\), sustituya −3 por x y −2 por y en la ecuación\(y = 2x + 5\).
\[ \begin{aligned} y = 2x + 5 ~ & \textcolor{red}{ \text{ Original equation.}} \\ −2 = 2(−3) + 5 ~ & \textcolor{red}{ \text{ Substitute: −3 for } x \text{ and } −2 \text{ for } y.} \\ −2 = −6+5 ~ & \textcolor{red}{ \text{ Multiply first: } 2(−3) = −6} \\ −2 = −1 ~ & \textcolor{red}{ \text{ Add: } −6+5= −1.} \end{aligned}\nonumber \]
Debido a que la declaración resultante es falsa, el par ordenado (−3, −2) no satisface la ecuación. El par ordenado (−3, −2) no es una solución de\(y = 2x + 5\).
a) Determinar si (5, 15) es una solución de\(y = 2x + 5\), sustituir 5 por x y 15 por y en la ecuación\(y = 2x + 5\).
\[ \begin{aligned} y = 2x + 5 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 15 = 2(5) + 5 ~ & \textcolor{red}{ \text{ Substitute: 5 for } x \text{ and } 15 \text{ for } y.} \\ 15 = 10 + 5 ~ & \textcolor{red}{ \text{ Multiply first: } 2(5) = 10} \\ 15 = 15 ~ & \textcolor{red}{ \text{ Add: } 10 + 5 = 15.} \end{aligned}\nonumber \]
La afirmación resultante es verdadera. El par ordenado (5, 15) sí satisface la ecuación. De ahí, (5, 15) es una solución de\(y = 2x + 5\).
Ejercicio
¿Cuáles de los pares ordenados (1, 7) y (2, 9) son solución de la ecuación\(y = 3x + 4\)?
- Contestar
-
(1, 7)
La Gráfica de una Ecuación
Volvemos nuestra atención a la gráfica de una ecuación.
La Gráfica de una Ecuación
La gráfica de una ecuación es el conjunto de todos los pares ordenados que son soluciones de la ecuación.
En la ecuación\(y = 2x + 5\), la variable y depende del valor de la variable x. Por esta razón, llamamos y la variable dependiente y x la variable independiente. Somos libres de tomar decisiones para x, pero el valor de y dependerá de nuestra elección para x.
También asignaremos el eje horizontal a la variable independiente x y el eje vertical a la variable dependiente y (ver Figura 8.7).
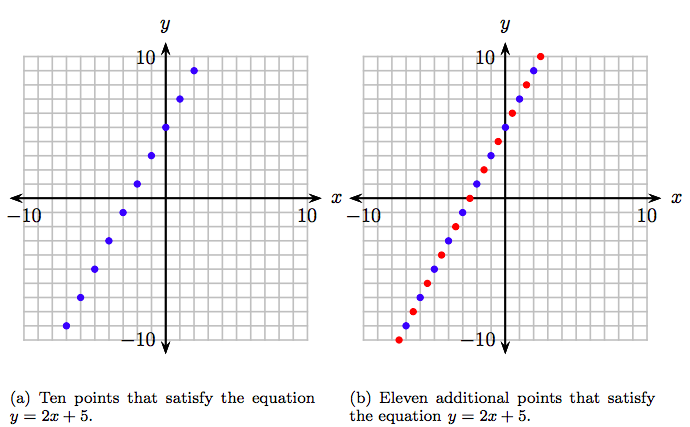
La gráfica de\(y = 2x+5\) consiste en todos los pares ordenados que son soluciones de la ecuación\(y = 2x+ 5\). Entonces, nuestra primera tarea es encontrar pares ordenados que sean soluciones de\(y = 2x + 5\). Esto se logra fácilmente seleccionando un número arbitrario de valores, sustituyéndolos por x en la ecuación\(y = 2x + 5\), luego calculando los valores resultantes de y. Con este pensamiento en mente, elegimos enteros arbitrarios −7, −6,.., 2, los sustituimos por x en la ecuación\(y = 2x + 5\), calcular el valor resultante de y, y almacenar los resultados en una tabla.
\[ \begin{array}{|r|r|r|r|} \hline y = 2x+5 & x & y & (x,~y) \\ \hline y = 2(−7) + 5 = −9 & −7 & −9 & (−7, −9) \\ y = 2(−6) + 5 = −7 & −6 & −7 & (−6, −7) \\ y = 2(−5) + 5 = −5 & −5 & −5 & (−5, −5) \\ y = 2(−4) + 5 = −3 & −4 & −3 & (−4, −3) \\ y = 2(−3) + 5 = −1 & −3 & −1 & (−3, −1) \\ y = 2(−2) + 5 = 1 & −2 & 1 & (−2, 1) \\ y = 2(−1) + 5 = 3 & −1 & 3 & (−1, 3) \\ y = 2(0) + 5 = 5 & 0 & 5 & (0, 5) \\ y = 2(1) + 5 = 7 & 1 & 7 & (1, 7) \\ y = 2(2) + 5 = 9 & 2 & 9 & (2, 9) \\ \hline \end{array}\nonumber \]
El resultado son 10 pares ordenados que satisfacen la ecuación\(y = 2x + 5\). Por lo tanto, tenemos 10 pares ordenados que pertenecen a la gráfica de\(y = 2x + 5\). Se trazan en la Figura 8.7 (a).
Sin embargo, no hemos terminado, porque la gráfica de la ecuación\(y = 2x + 5\) es el conjunto de todos los puntos que satisfacen la ecuación y sólo hemos trazado 10 de esos puntos. Vamos a trazar algunos puntos más. Seleccione algunos valores x más, calcule el valor y correspondiente y registre los resultados en una tabla.
\[ \begin{array}{|r|r|r|r|} \hline y = 2x + 5 & x & y & (x, y) \\ \hline y = 2(−7.5) + 5 = −10 & −7.5 & −10 & (−7.5, −10) \\ y = 2(−6.5) + 5 = −8 & −6.5 & −8 & (−6.5, −8) \\ y = 2(−5.5) + 5 = −6 & −5.5 & −6 & (−5.5, −6) \\ y = 2(−4.5) + 5 = −4 & −4.5 & −4 & (−4.5, −4) \\ y = 2(−3.5) + 5 = −2 & −3.5 & −2 & (−3.5, −2) \\ y = 2(−2.5) + 5 = 0 & −2.5 & 0 & (−2.5, 0) \\ y = 2(−1.5) + 5 = 2 & −1.5 & 2 & (−1.5, 2) \\ y = 2(−0.5) + 5 = 4 & −0.5 & 4 & (−0.5, 4) \\ y = 2(0.5) + 5 = 6 & 0.5 & 6 & (0.5, 6) \\ y = 2(1.5) + 5 = 8 & 1.5 & 8 & (1.5, 8) \\ y = 2(2.5) + 5 = 10 & 2.5 & 10 & (2.5, 10) \\ \hline \end{array}\nonumber \]
Eso son 11 puntos adicionales que agregamos a la gráfica de la Figura 8.7 (b).
Tenga en cuenta que podemos continuar indefinidamente de esta manera, sumando puntos a la tabla y trazándolos. No obstante, tarde o temprano, tenemos que dar un salto de fe, e imaginar cómo será la gráfica final cuando se trazen todos los puntos que satisfacen la ecuación y = 2x+ 5. Lo hacemos en la Figura 8.8, donde la gráfica final toma la apariencia de una línea.
Uso de regla
Todas las líneas deben ser dibujadas con una regla. Esto incluye los ejes x e y.
Observación Importante. Cuando usamos una regla para dibujar una línea a través de los puntos trazados en la Figura 8.7 (b), llegando al resultado final en la Figura 8.8, debemos entender que esta es una técnica de atajo para trazar todos los pares ordenados restantes que satisfacen la ecuación. Realmente no estamos dibujando una línea a través de los puntos trazados. Más bien, estamos sombreando todos los pares ordenados que satisfacen la ecuación\(y = 2x + 5\).
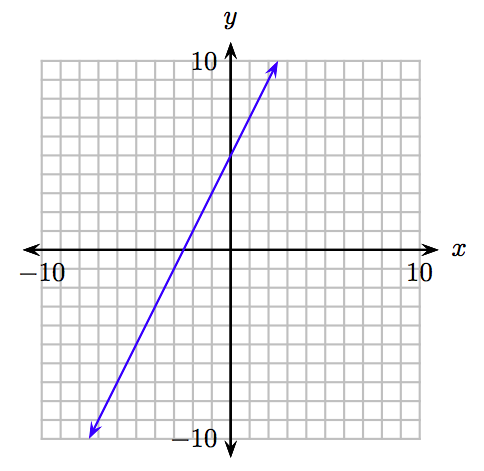
El Resultado. El gráfico de la ecuación\(y = 2x + 5\), representado en la Figura 8.8, es una línea. En realidad, la gráfica es una colección infinita de puntos que satisfacen la ecuación\(y = 2x + 5\) que toma la forma de una línea, pero está bien decir que la gráfica de\(y = 2x + 5\) es una línea.
Pares Ordenados y la Gráfica
Debido a que la gráfica de una ecuación es la colección de todos los pares ordenados que satisfacen la ecuación, tenemos dos resultados importantes:
- Si un par ordenado satisface una ecuación, entonces el punto en el plano cartesiano representado por el par ordenado está en la gráfica de la ecuación.
- Si un punto está en la gráfica de una ecuación, entonces la representación de par ordenado de ese punto satisface la ecuación.
Ejemplo 2
Encuentra el valor de k para que el punto (2, k) esté en la gráfica de la ecuación\(y = 3x − 2\).
Solución
Si el punto (2, k) está en la gráfica de\(y = 3x−2\), entonces debe satisfacer la ecuación\(y = 3x − 2\).
\[ \begin{aligned} y = 3x − 2 ~ & \textcolor{red}{ \text{ Original equation.}} \\ k = 3(2) − 2 ~ & \begin{array}{l} \textcolor{red}{ \text{ The point (2, } k) \text{ is on the graph.}} \\ \textcolor{red}{ \text{ Substitute 2 for } x \text{ and } k \text{ for } y \text{ in } y = 3x − 2.} \end{array} \\ k = 6 − 2 ~ & \textcolor{red}{ \text{ Multiply: } 3(2) = 6.} \\ k = 4 ~ & \textcolor{red}{ \text{ Subtract: } 6 − 2 = 4.} \end{aligned}\nonumber \]
Así, k = 4.
Ejercicio
Encuentra el valor de k para que el punto (k, −3) esté en la gráfica de la ecuación\(y = 4x + 2\).
- Contestar
-
k = −5/4
Ecuaciones Lineales
Vamos a trazar la gráfica de otra ecuación.
Ejemplo 3
Esbozar la gráfica de\(y = −2x + 1\).
Solución
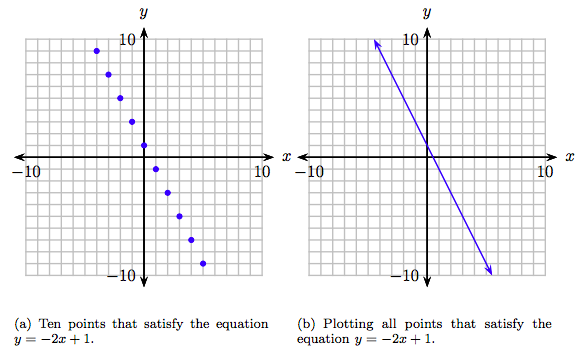
Seleccionar valores arbitrarios de x: −4, −3,.., 5. Sustituya estos valores en la ecuación\(y = −2x + 1\), calcule el valor resultante de y, luego, organice sus resultados en una tabla.
\[ \begin{array}{|r|r|r|r|} \hline y = −2x + 1 & x & y & (x, y) \\ \hline y = −2(−4) + 1 = 9 & −4 & 9 & (−4, 9) \\ y = −2(−3) + 1 = 7 & −3 & 7 & (−3, 7) \\ y = −2(−2) + 1 = 5 & −2 & 5 & (−2, 5) \\ y = −2(−1) + 1 = 3 & −1 & 3 & (−1, 3) \\ y = −2(0) + 1 = 1 & 0 & 1 & (0, 1) \\ y = −2(1) + 1 = −1 & 1 & −1 & (1, −1) \\ y = −2(2) + 1 = −3 & 2 & −3 & (2, −3) \\ y = −2(3) + 1 = −5 & 3 & −5 & (3, −5) \\ y = −2(4) + 1 = −7 & 4 & −7 & (4, −7) \\ y = −2(5) + 1 = −9 & 5 & −9 & (5, −9) \\ \hline \end{array}\nonumber \]
Hemos trazado los puntos en la tabla en la Figura 8.9 (a). Hay suficiente evidencia en la Figura 8.9 (a) para imaginar que si trazamos todos los puntos que satisfacían la ecuación\(y = −2x + 1\), el resultado sería la línea que se muestra en la Figura 8.9 (b).
Ejercicio
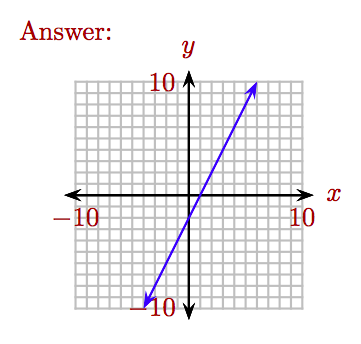
Esbozar la gráfica de\(y = 2x − 2\).
- Contestar
-
La gráfica de\(y = 2x + 5\) la Figura 8.8 es una línea. La gráfica de\(y = −2x + 1\) la Figura 8.9 (b) es también una línea. Esto llevaría a sospechar que la gráfica de la ecuación\(y = mx+b\), donde m y b son constantes, siempre será una línea. En efecto, este es siempre el caso.
Ecuaciones Lineales
La gráfica de\(y = mx + b\), donde m y b son constantes, siempre será una línea. Por esta razón, la ecuación\(y = mx+b\) se denomina ecuación lineal.
Ejemplo 4
¿Cuál de las siguientes ecuaciones es una ecuación lineal? 1. \(y = −3x + 4\), 2. \(y = \frac{2}{3}x + 3\), y 3. \(y = 2x^2 + 4\).
Solución
Comparar cada ecuación con la forma general de una ecuación lineal,\(y = mx + b\).
- Tenga en cuenta que\(y = −3x + 4\) tiene la forma\(y = mx + b\), donde m = −3 y b = 4. De ahí,\(y = −3x + 4\) es una ecuación lineal. Su gráfica es una línea.
- Tenga en cuenta que\(y = \frac{2}{3} x+ 3\) tiene la forma\(y = mx+b\), donde m = 2/3 y b = 3. De ahí,\(y = \frac{2}{3} x + 3\) es una ecuación lineal. Su gráfica es una línea.
- La ecuación\(y = 2x^2 + 4\) no tiene la forma\(y = mx + b\). El exponente de 2 sobre la x evita que esta ecuación sea lineal. Esta es una ecuación no lineal. Su gráfica no es una línea.
Ejercicio
¿Cuál de las siguientes ecuaciones es una ecuación lineal? a)\(y = 2x^3 + 5\) b)\(y= -3x-5\)
- Contestar
-
\(y = −3x − 5\)
El hecho de que\(y = mx + b\) sea una ecuación lineal nos permite esbozar rápidamente su gráfica.
Ejemplo 5
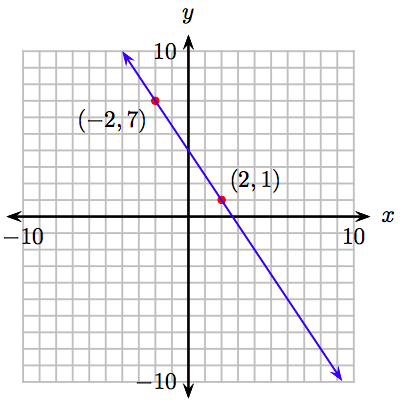
Esbozar la gráfica de\(y = − \frac{3}{2} x + 4\).
Solución
La ecuación\(y = −3 2x+ 4\) tiene la forma\(y = mx+b\). Por lo tanto, la ecuación es lineal y la gráfica será una línea. Debido a que dos puntos determinan una línea, solo necesitamos encontrar dos puntos que satisfagan la ecuación\(y = − \frac{3}{2} x + 4\), trazarlos, luego dibujar una línea a través de ellos con una regla. Elegimos x = −2 y x = 2, calculamos y y registramos los resultados en una tabla.
\[ \begin{array}{|r|r|r|r|} \hline y = − \frac{3}{2} x + 4 & x & y & (x, y) \\ \hline y = − \frac{3}{2} (−2) + 4 = 3 + 4 = 7 & −2 & 7 & (−2, 7) \\ y = − \frac{3}{2} (2) + 4 = −3+4=1 & 2 & 1 & (2, 1) \\ \hline \end{array}\nonumber \]
Traza los puntos (−2, 7) y (2, 1) y dibuja una línea a través de ellos. El resultado se muestra en la Figura 8.10.
Ejercicio
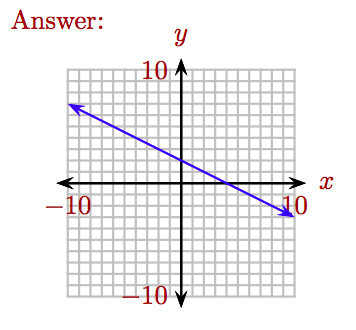
Esbozar la gráfica de\(y = − \frac{1}{2} x + 2\).
- Contestar
-
Es posible que haya notado en el Ejemplo 5 que son opciones de −2 y 2 para x aligeraron el cálculo de los valores y correspondientes debido a la cancelación resultante.
Elección de Valores Estratégicos
Al trazar una ecuación lineal, es una buena estrategia elegir valores de x que simplifiquen el cálculo de los valores y correspondientes.
Ejemplo 6
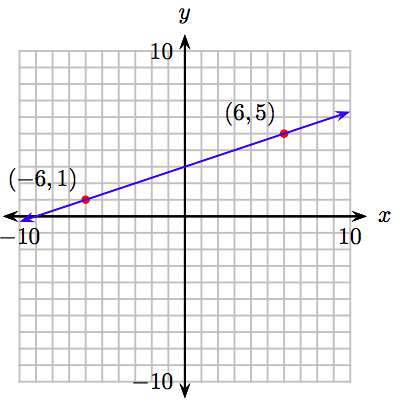
Dibuja la gráfica de y =\ frac {1} {3} x + 3.
Solución
La ecuación\(y = \frac{1}{3} x + 3\) tiene la forma\(y = mx + b\). Por lo tanto, la ecuación es lineal y la gráfica será una línea. Debido a que dos puntos determinan una línea, solo necesitamos encontrar dos puntos que satisfagan la ecuación y = 1 3x + 3, trazarlos, luego dibujar una línea a través de ellos con una regla. Elegimos x = −6 y x = 6, calculamos y y registramos los resultados en una tabla.
\[ \begin{array}{|r|r|r|r|} \hline y = \frac{1}{3} x + 3 & x & y & (x, y) \\ \hline y = \frac{1}{3} (−6) + 3 = −2+3=1 & −6 & 1 & (−6, 1) \\ y = \frac{1}{3} (6) + 3 = 2 + 3 = 5 & 6 & 5 & (6, 5) \\ \hline \end{array}\nonumber \]
Traza los puntos (−6, 1) y (6, 5) y dibuja una línea a través de ellos. El resultado se muestra en la Figura 8.11.
Ejercicio
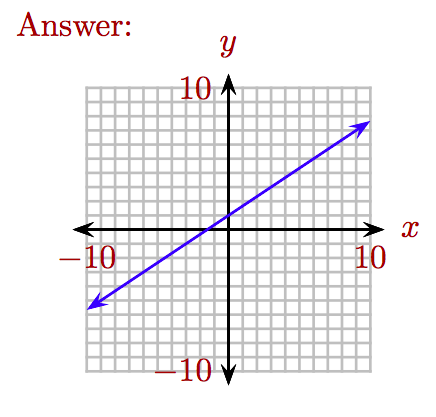
Esbozar la gráfica de\(y = \frac{2}{3} x + 1\).
- Contestar
-
Ejercicios
1. ¿Cuál de los puntos (2, −14), (−1, −6), (−8, 11) y (3, −13) es una solución de la ecuación\(y = −2x − 8\)?
2. ¿Cuál de los puntos (1, −2), (8, 23), (−3, −23) y (8, 24) es una solución de la ecuación\(y = 4x − 9\)?
3. ¿Cuál de los puntos (1, −1), (−2, 20), (−4, 31) y (−9, 64) es una solución de la ecuación\(y = −6x + 7\)?
4. ¿Cuál de los puntos (−8, −61), (4, 42), (−3, −18) y (−6, −46) es una solución de la ecuación\(y = 9x + 8\)?
5. ¿Cuál de los puntos (2, 15), (−8, −74), (2, 18) y (5, 40) es una solución de la ecuación\(y = 9x − 3\)?
6. ¿Cuál de los puntos (−9, −52), (−8, −44), (−7, −37) y (8, 35) es una solución de la ecuación\(y = 5x − 5\)?
7. ¿Cuál de los puntos (−2, 12), (−1, 12), (3, −10) y (−2, 14) es una solución de la ecuación\(y = −5x + 4\)?
8. ¿Cuál de los puntos (6, 25), (−8, −14), (8, 33) y (−7, −9) es una solución de la ecuación\(y = 3x + 9\)?
9. Determinar k para que el punto (9, k) sea una solución de\(y = −6x + 1\).
10. Determinar k para que el punto (−9, k) sea una solución de\(y = 2x + 3\).
11. Determinar k para que el punto (k, 7) sea una solución de\(y = −4x + 1\).
12. Determinar k para que el punto (k, −4) sea una solución de\(y = 8x + 3\).
13. Determinar k para que el punto (k, 1) sea una solución de\(y = 4x + 8\).
14. Determinar k para que el punto (k, −7) sea una solución de\(y = −7x + 5\).
15. Determinar k para que el punto (−1, k) sea una solución de\(y = −5x + 3\).
16. Determinar k para que el punto (−3, k) sea una solución de\(y = 3x + 3\).
En los Ejercicios 17-24, ¿cuál de las ecuaciones dadas es una ecuación lineal?
17. \(y = 6x^2 + 4, ~ y = x^2 + 6x + 4, ~ y = 6x + 4, ~ y = \sqrt{6x + 4}\)
18. \(y = −2x + 1, ~ y = x^2 − 2x + 1, ~ y = \sqrt{−2x + 1}, ~ y = −2x^2 + 1\)
19. \(y = x + 7, ~ y = \sqrt{x + 7}, ~ y = x^2 + 7, ~ y = x^2 + x + 7\)
20. \(y = x^2 + 5x + 1, ~ y = 5x^2 + 1, ~ y = \sqrt{5x + 1}, ~ y = 5x + 1\)
21. \(y = x^2 − 2x − 2, ~ y = −2x^2 − 2, ~ y = \sqrt{−2x − 2}, ~ y = −2x − 2\)
22. \(y = x^2 + 5x − 8, ~ y = 5x^2 − 8, ~ y = \sqrt{5x − 8}, ~ y = 5x − 8\)
23. \(y = x^2 + 7x − 3, ~ y = 7x^2 − 3, ~ y = 7x − 3, ~ y = \sqrt{7x − 3}\)
24. \(y = \sqrt{−4x − 3}, ~ y = x^2 − 4x − 3, ~ y = −4x − 3, ~ y = −4x^2 − 3\)
En los Ejercicios 25-28, ¿cuál de las ecuaciones dadas tiene la gráfica dada?
25. \(y = − \frac{3}{2}x + 2, ~ y = \frac{3}{2} x − 3, ~ y = −3x + 1, ~ y = −2x + 1\)
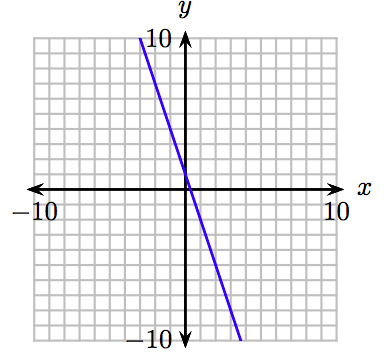
26. \(y = −3x − 2, ~ y = \frac{3}{2} x + 1, ~ y = −2x − 1, ~ y = \frac{5}{2}x + \)2
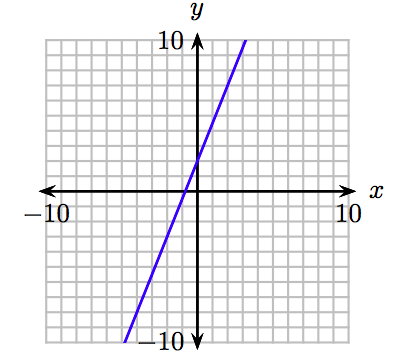
27. \(y = \frac{5}{2} x − 2, ~ y = 3x + 3, ~ y = \frac{3}{2} x + 1, ~ y = \frac{1}{2} x + 1\)
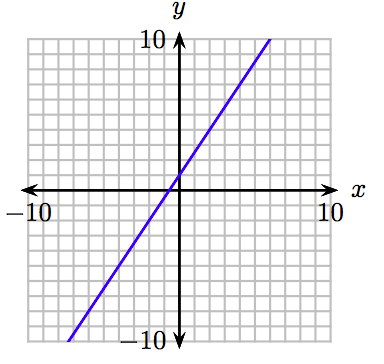
28. \(y = 3x + 1, ~ y = \frac{5}{2} x − 1, ~ y = − \frac{5}{2} x − 3, ~ y = \frac{3}{2} x − 2\)
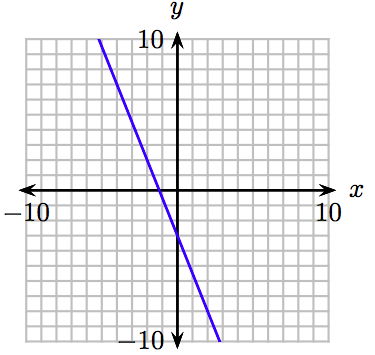
29. \(y = 3x − 2\)
30. \(y = \frac{5}{2}x + 1\)
31. \(y = −2x − 1\)
32. \(y = \frac{5}{2} x + 2\)
33. \(y = −2x + 2\)
34. \(y = − \frac{5}{2}x − 2\)
35. \(y = −2x − 2\)
36. \(y = − \frac{5}{2}x + 1\)
37. \(y = 2x − 2\)
38. \(y = \frac{5}{2} x − 1\)
39. \(y = \frac{3}{2}x + 1\)
40. \(y = 2x + 2\)
41. \(y = 2x − 3\)
42. \(y = − \frac{5}{2}x − 1\)
43. \(y = \frac{3}{2}x + 3\)
44. \(y = 3x + 1\)
45. Dibuja las líneas\(y = \frac{1}{2} x−1\) y\(y = \frac{5}{2} x−2\) en papel cuadriculado. Al barrer los ojos de izquierda a derecha, ¿qué línea se eleva más rápido?
46. Dibuja las líneas\(y = \frac{5}{2} x+ 1\) y\(y = 3x+ 1\) en papel cuadriculado. Al barrer los ojos de izquierda a derecha, ¿qué línea se eleva más rápido?
47. Dibuje la línea\(y = − \frac{1}{2} x + 1\) y\(y = −3x+ 3\). Al barrer los ojos de izquierda a derecha, ¿qué línea cae más rápido?
48. Dibuje la línea\(y = −3x − 1\) y\(y = − \frac{5}{2} x−2\). Al barrer los ojos de izquierda a derecha, ¿qué línea cae más rápido?
49. Dibuje la línea\(y = −3x − 1\) y\(y = − \frac{1}{2} x−2\). Al barrer los ojos de izquierda a derecha, ¿qué línea cae más rápido?
50. Dibuje la línea\(y = −3x − 1\) y\(y = − \frac{1}{2}x+1\). Al barrer los ojos de izquierda a derecha, ¿qué línea cae más rápido?
51. Dibuja las líneas\(y = \frac{3}{2} x−2\) y\(y = 3x+ 1\) en papel cuadriculado. Al barrer los ojos de izquierda a derecha, ¿qué línea se eleva más rápido?
52. Dibuja las líneas\(y = \frac{1}{2} x+ 3\) y\(y = \frac{5}{2}x+ 1\) en papel cuadriculado. Al barrer los ojos de izquierda a derecha, ¿qué línea se eleva más rápido?
RESPUESTAS
1. (−1, −6)
3. (−4, 31)
5. (2, 15)
7. (−2, 14)
9. k = −53
11. k =\(− \frac{3}{2}\)
13. k =\(− \frac{7}{4}\)
15. k = 8
17. \(y = 6x + 4\)
19. \(y = x + 7\)
21. \(y = −2x − 2\)
23. \(y = 7x − 3\)
25. \(y = −3x + 1\)
27. \(y = \frac{3}{2} x + 1\)
29. \(y = 3x − 2\)
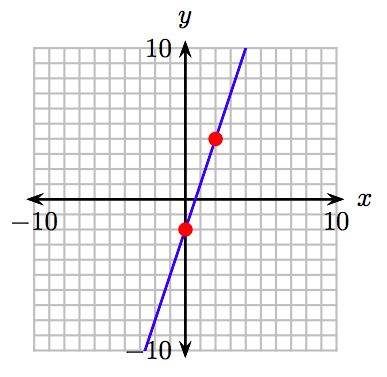
31. \(y = −2x − 1\)
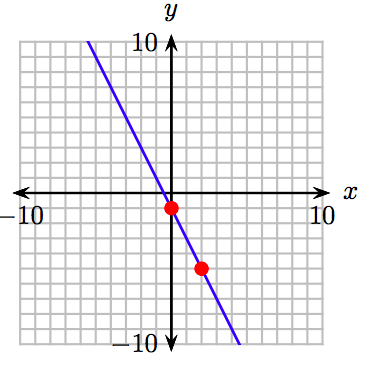
33. \(y = −2x + 2\)
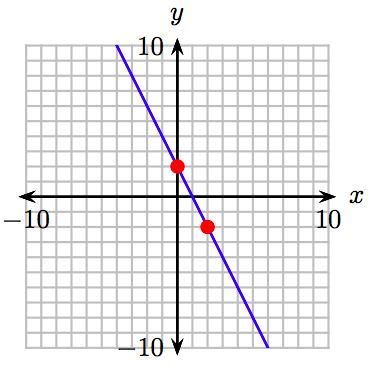
35. \(y = −2x -2\)
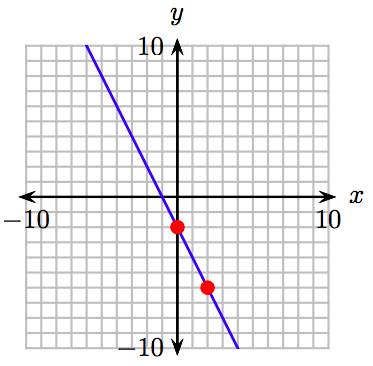
37. \(y = 2x-2\)
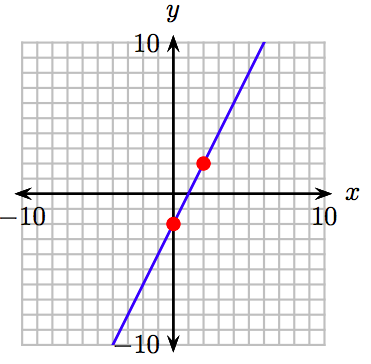
39. \(y = \frac{3}{2} + 1\)
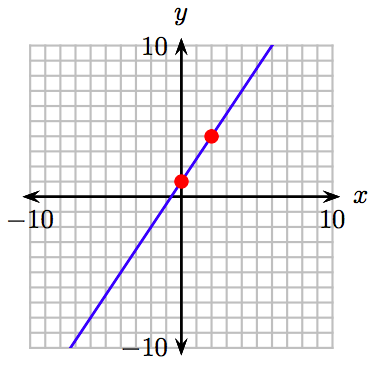
41. \(y = 2x − 3\)
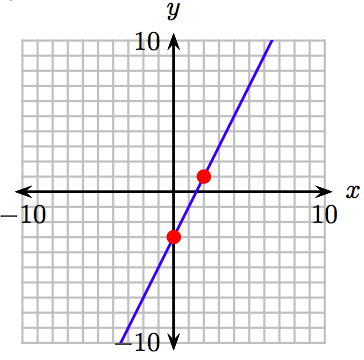
43. \(y = \frac{3}{2} x + 3\)
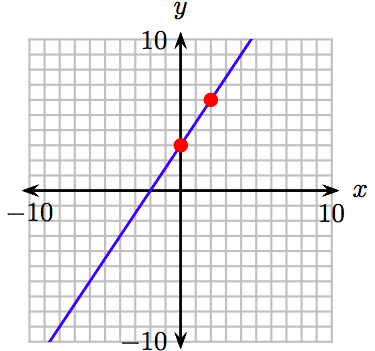
45. La gráfica de\(y = \frac{5}{2} x−2\) sube más rápidamente.
47. El gráfico de\(y = −3x + 3\) caídas más rápido.
49. El gráfico de\(y = −3x − 1\) caídas más rápido.
51. La gráfica de\(y = 3x+1\) sube más rápidamente.


