8.2: El sistema de coordenadas cartesianas

Última actualización
Guardar como PDF

Page ID: 113444

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Comencemos con el concepto de un par ordenado de números enteros.

Pares ordenados de números enteros

El constructo (x, y), donde x e y son números enteros, se denomina par ordenado de números enteros.

Ejemplos de pares ordenados de números enteros son (0, 0), (2, 3), (5, 1) y (4, 9).

Asuntos de orden

Preste especial atención a la frase “pares ordenados”. Cuestiones de orden. En consecuencia, el par ordenado (x, y) no es lo mismo que el par ordenado (y, x), porque los números se presentan en un orden diferente.

Hemos visto cómo trazar números enteros en una recta numérica. Por ejemplo, en la Figura 8.1, hemos trazado los números enteros 2, 5 y 7 como “puntos” sombreados en la recta numérica.

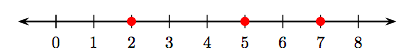
Screen Shot 2019-09-27 a las 2.29.55 PM.png — Figura 8.1: Trazar los números enteros 2, 5 y 7 en una recta numérica.

Para trazar pares ordenados, necesitamos dos líneas numéricos, llamadas ejes horizontal y vertical, que se cruzan en la ubicación cero de cada línea y están en ángulo recto entre sí, como se muestra en la Figura 8.2 (a). El punto donde tocan las ubicaciones cero se denomina origen del sistema de coordenadas y tiene coordenadas (0, 0). En la Figura 8.2 (b), hemos agregado una cuadrícula. El constructo resultante es un ejemplo de un Sistema de Coordenadas Cartesianas.

Screen Shot 2019-09-27 en 2.30.01 PM.png — Figura 8.2: Un sistema de coordenadas cartesianas.

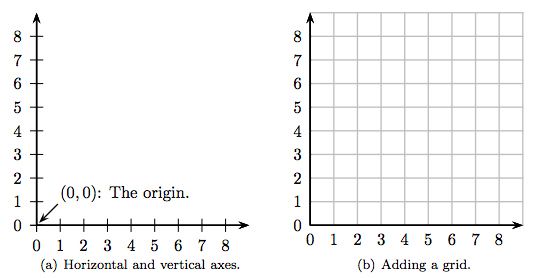
Ahora, considere el par ordenado de números enteros (5, 6). Para trazar este punto en el “sistema de coordenadas” de la Figura 8.3 (a), comience en el origen (0, 0), luego mueva 5 unidades en dirección horizontal, luego 6 unidades en dirección vertical, luego trazar un punto. El resultado se muestra en la Figura 8.3 (a). Agregar una cuadrícula de líneas horizontales y verticales en cada número entero hace que trazar el punto (5, 6) sea mucho más claro, como se muestra en la Figura 8.3 (b).

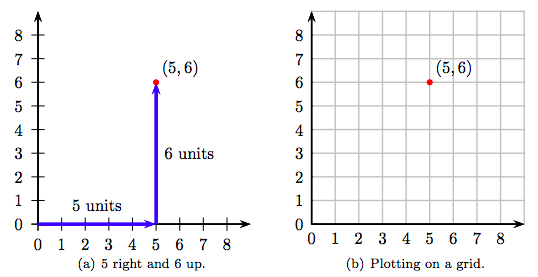
Screen Shot 2019-09-27 en 2.30.55 PM.png — Figura 8.3: Trazando el Punto (5, 6) en un Sistema de Coordenadas Cartesianas.

Los números en el par ordenado (5, 6) se denominan las coordenadas del punto trazado en la Figura 8.3 (b). El primer número del par ordenado se llama abscisa y mide la distancia horizontal al punto trazado. El segundo número se llama la ordenada y mide la distancia vertical al punto trazado. La combinación de ejes y cuadrícula en la Figura 8.3 (b) se denomina sistema de coordenadas.

La cuadrícula de la Figura 8.3 (b) es una visualización que facilita enormemente el trazado de pares ordenados. Sin embargo, no tienes que dibujar estas líneas de cuadrícula tú mismo. En cambio, deberías trabajar en papel cuadriculado.

Requisito de Papel Grafico

Todo el trazado debe hacerse en papel cuadriculado.

Ejemplo 1

Trazar los siguientes pares ordenados de números enteros: (3, 2), (8, 6) y (2, 7).

Solución

Cree un sistema de coordenadas cartesianas en papel cuadriculado, luego:

Para trazar el par ordenado (3, 2), comenzar en el origen, luego mover 3 unidades a la derecha y 2 unidades hacia arriba.
Para trazar el par ordenado (8, 6), comenzar en el origen, luego mover 8 unidades a la derecha y 6 unidades hacia arriba.
Para trazar el par ordenado (2, 7), comenzar en el origen, luego mover 2 unidades a la derecha y 7 unidades hacia arriba.

Los resultados se muestran en el siguiente sistema de coordenadas cartesianas.

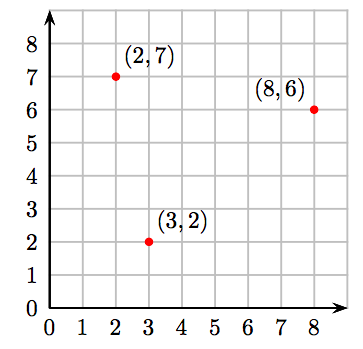
$Screen Shot 2019-09-27 en 1.58.14 PM.png$

Ejercicio

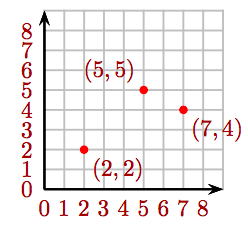
Trazar los siguientes pares ordenados de números enteros: (2, 2), (5, 5) y (7, 4).

Responder: $Capturación 2019-09-27 en 1.58.08 PM.png$

Permitir números negativos

Nuevamente, hemos visto cómo trazar números tanto positivos como negativos en una recta numérica. Por ejemplo, en la Figura 8.4, hemos trazado los números −4, −3/2, 2.2 y 4.

Screen Shot 2019-09-27 en 1.59.24 PM.png — Figura 8.4: Trazando los números −4, −3/2, 2.2 y 4.

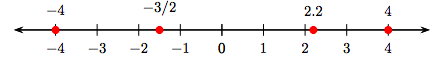
Obsérvese que la dirección positiva es hacia la derecha, la negativa hacia la izquierda. Es decir, para trazar el número 2.2, movemos 2.2 unidades a la derecha en la línea, pero para trazar el número −3/2, movemos 3/2 unidades a la izquierda.

Para trazar pares ordenados que tengan números tanto positivos como negativos, necesitamos dos líneas numéricos de este tipo que se cruzan en la ubicación cero de cada línea y están en ángulo recto entre sí, como se muestra en la Figura 8.5 (a). Como antes, agregar una cuadrícula de líneas horizontales y verticales en cada entero será de gran ayuda a la hora de trazar puntos (ver Figura 8.5 (b)). El sistema de ejes y cuadrícula en la Figura 8.5 (b) se denomina Sistema de Coordenadas Cartesianas, que lleva el nombre de su inventor, René Descartes.

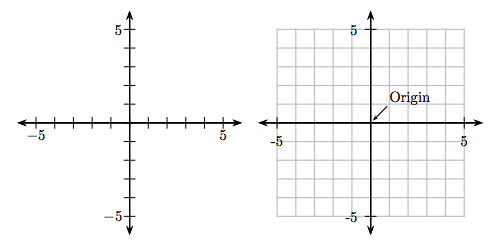
Screen Shot 2019-09-27 en 1.59.33 PM.png — Figura 8.5: El sistema de coordenadas cartesianas.

Trazado de puntos en el sistema de coordenadas cartesianas

En el eje horizontal, la dirección positiva es hacia la derecha, negativa es hacia la izquierda. En el eje vertical, la dirección positiva es hacia arriba, la negativa es hacia abajo. El punto (0, 0) se denomina origen del sistema de coordenadas, y es el punto de partida para todo el trazado de puntos.

Ejemplo 2

Esboce los puntos (4, 3), (−3, 2), (−2, −4) y (3, −3) en un sistema de coordenadas cartesianas.

Solución

Configure un sistema de coordenadas cartesianas en papel cuadriculado.

Para trazar el punto (4, 3), comience en el origen, mueva 4 unidades a la derecha, luego 3 unidades hacia arriba.
Para trazar el punto (−3, 2), comienza en el origen, mueve 3 unidades hacia la izquierda, luego 2 unidades hacia arriba.
Para trazar el punto (−2, −4), comienza en el origen, mueve 2 unidades hacia la izquierda, luego 4 unidades hacia abajo.
Para trazar el punto (3, −3), comienza en el origen, mueve 3 unidades a la derecha, luego 3 unidades hacia abajo.

Estos puntos se trazan y se muestran en la Figura 8.6.

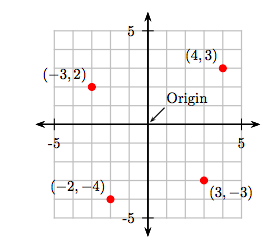
Screen Shot 2019-09-27 en 1.59.43 PM.png — Figura 8.6: Trazando puntos en el sistema de coordenadas cartesianas.

Ejercicio

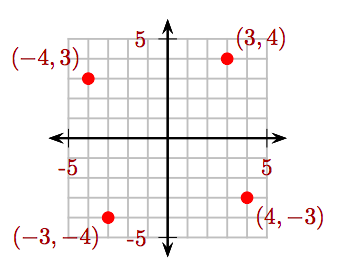
Esboce los puntos (3, 4), (−4, 3), (−3, −4) y (4, −3) en un sistema de coordenadas cartesianas.

Responder: $Screen Shot 2019-09-27 en 1.59.52 PM.png$

Ejemplo 3

¿Cuáles son las coordenadas de los puntos P, Q, R y S en el sistema de coordenadas cartesianas que siguen?

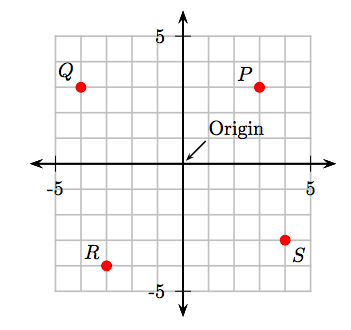
$Screen Shot 2019-09-27 a las 2.00.02 PM.png$

Solución

Realizar todas las medidas desde el origen.

Para obtener las coordenadas del punto P, comience en el origen, mueva 3 unidades a la derecha, luego 3 unidades hacia arriba. De ahí que las coordenadas del punto P sean (3, 3).
Para obtener las coordenadas del punto Q, inicia en el origen, mueve 4 unidades hacia la izquierda, luego 3 unidades hacia arriba. De ahí que las coordenadas del punto Q sean (−4, 3).
Para obtener las coordenadas del punto R, comience en el origen, mueva 3 unidades hacia la izquierda, luego 4 unidades hacia abajo. De ahí que las coordenadas del punto R sean (−3, −4).
Para obtener las coordenadas del punto S, comience en el origen, mueva 4 unidades a la derecha, luego 3 unidades hacia abajo. De ahí que las coordenadas del punto S sean (4, −3).

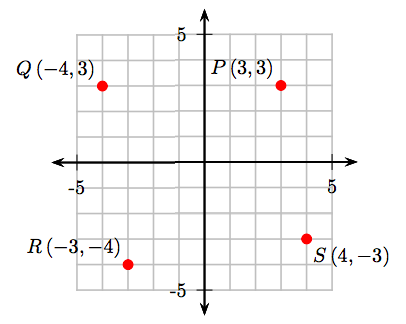
Estos resultados se muestran en el siguiente sistema de coordenadas cartesianas.

$Screen Shot 2019-09-27 a las 2.00.12 PM.png$

Ejercicios

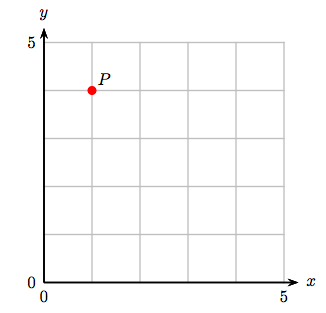
1. Identificar las coordenadas del punto P.

$Screen Shot 2019-09-27 a las 2.22.07 PM.png$

2. Identificar las coordenadas del punto P.

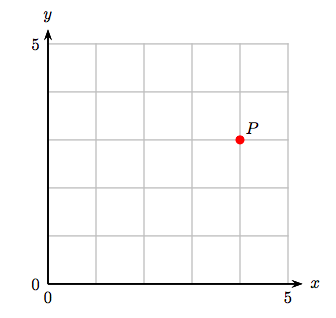
$Screen Shot 2019-09-27 en 2.22.21 PM.png$

3. Identificar las coordenadas del punto P.

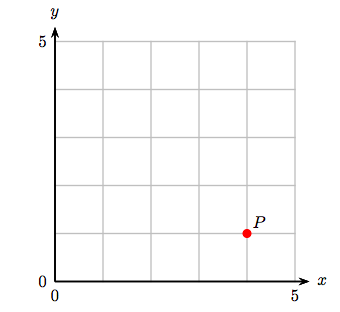
$Screen Shot 2019-09-27 en 2.22.26 PM.png$

4. Identificar las coordenadas del punto P.

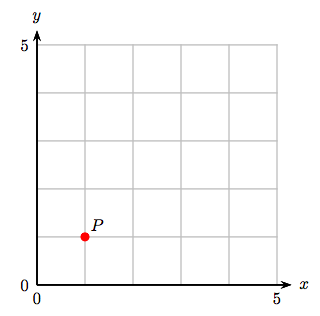
$Screen Shot 2019-09-27 en 2.22.32 PM.png$

5. Identificar las coordenadas del punto P.

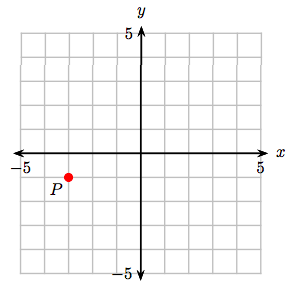
$Screen Shot 2019-09-27 en 2.22.39 PM.png$

6. Identificar las coordenadas del punto P.

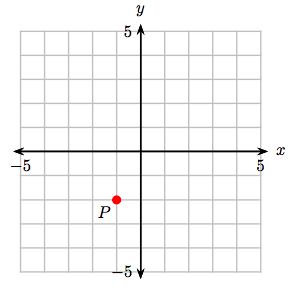
$Screen Shot 2019-09-27 en 2.22.44 PM.png$

7. Identificar las coordenadas del punto P.

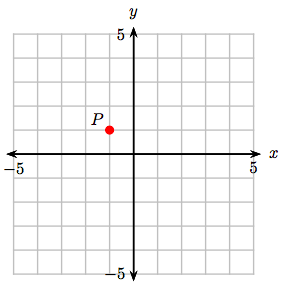
$Screen Shot 2019-09-27 a las 2.22.50 PM.png$

8. Identificar las coordenadas del punto P.

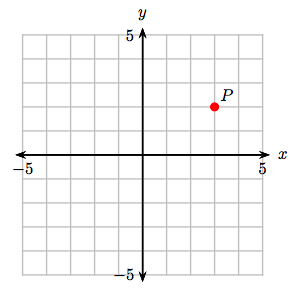
$Screen Shot 2019-09-27 en 2.22.56 PM.png$

9. Los puntos A (−1, 1), B (1, 1), C (1, 2) y D (−1, 2) son los vértices de un rectángulo. Traza estos puntos, dibuja el rectángulo ABCD, luego calcula el área del rectángulo ABCD.

10. Los puntos A (−3, −4), B (4, −4), C (4, −1) y D (−3, −1) son los vértices de un rectángulo. Traza estos puntos, dibuja el rectángulo ABCD, luego calcula el área del rectángulo ABCD.

11. Los puntos A (−2, −1), B (3, −1), C (3, 3) y D (−2, 3) son los vértices de un rectángulo. Traza estos puntos, dibuja el rectángulo ABCD, luego calcula el área del rectángulo ABCD.

12. Los puntos A (−3, −1), B (2, −1), C (2, 2) y D (−3, 2) son los vértices de un rectángulo. Traza estos puntos, dibuja el rectángulo ABCD, luego calcula el área del rectángulo ABCD.

13. Los puntos A (−4, −2), B (1, −2), C (1, 1) y D (−4, 1) son los vértices de un rectángulo. Trazar estos puntos, dibujar el rectángulo ABCD, luego calcular el perímetro del rectángulo ABCD.

14. Los puntos A (−4, −4), B (1, −4), C (1, −3) y D (−4, −3) son los vértices de un rectángulo. Trazar estos puntos, dibujar el rectángulo ABCD, luego calcular el perímetro del rectángulo ABCD.

15. Los puntos A (−1, 2), B (3, 2), C (3, 3) y D (−1, 3) son los vértices de un rectángulo. Trazar estos puntos, dibujar el rectángulo ABCD, luego calcular el perímetro del rectángulo ABCD.

16. Los puntos A (−4, 2), B (3, 2), C (3, 4) y D (−4, 4) son los vértices de un rectángulo. Trazar estos puntos, dibujar el rectángulo ABCD, luego calcular el perímetro del rectángulo ABCD.

17. Los puntos A (−3, −1), B (1, −1) y C (−3, 0) son los vértices de un triángulo. Traza estos puntos, dibuja el triángulo ABC, luego calcula el área del triángulo ABC.

18. Los puntos A (−3, −2), B (1, −2) y C (−3, 2) son los vértices de un triángulo. Traza estos puntos, dibuja el triángulo ABC, luego calcula el área del triángulo ABC.

19. Los puntos A (−1, −2), B (0, −2) y C (−1, 0) son los vértices de un triángulo. Traza estos puntos, dibuja el triángulo ABC, luego calcula el área del triángulo ABC.

20. Los puntos A (−2, −3), B (−1, −3) y C (−2, 1) son los vértices de un triángulo. Traza estos puntos, dibuja el triángulo ABC, luego calcula el área del triángulo ABC.

21. Traza los puntos A (−3, −3) y B (0, 0) y encuentra la distancia en línea recta entre los dos puntos. Pista: Crea un triángulo rectángulo, luego usa el Teorema de Pitágoras.

22. Traza los puntos A (−2, −3) y B (1, 2) y encuentra la distancia en línea recta entre los dos puntos. Pista: Crea un triángulo rectángulo, luego usa el Teorema de Pitágoras.

23. Traza los puntos A (−2, −3) y B (0, 0) y encuentra la distancia en línea recta entre los dos puntos. Pista: Crea un triángulo rectángulo, luego usa el Teorema de Pitágoras.

24. Traza los puntos A (−3, −2) y B (2, 2) y encuentra la distancia en línea recta entre los dos puntos. Pista: Crea un triángulo rectángulo, luego usa el Teorema de Pitágoras.

25. Encuentra el área del triángulo sombreado.

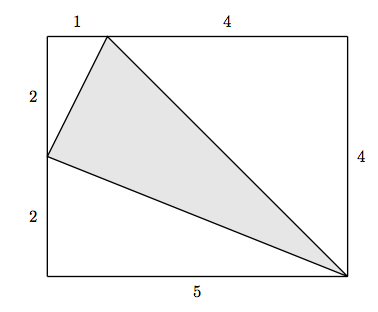
$Screen Shot 2019-09-27 en 2.10.48 PM.png$

26. Encuentra el área del triángulo sombreado.

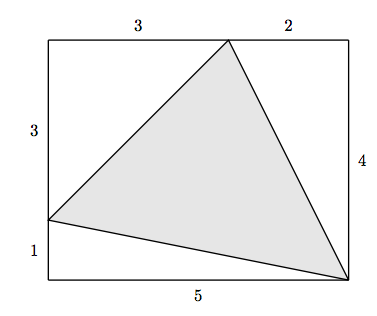
$Screen Shot 2019-09-27 en 2.10.54 PM.png$

27. Encuentra el área del triángulo sombreado.

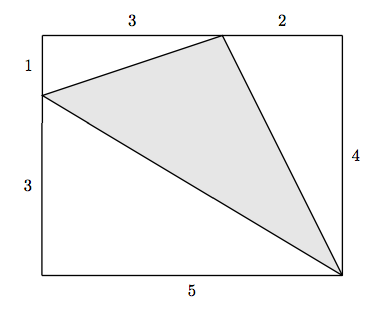
$Screen Shot 2019-09-27 en 2.10.59 PM.png$

28. Encuentra el área del triángulo sombreado.

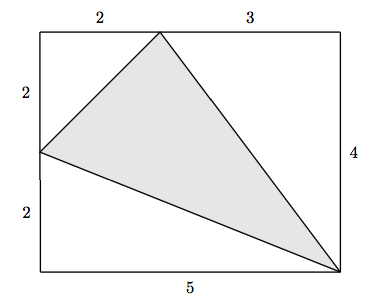
$Screen Shot 2019-09-27 en 2.11.03 PM.png$

Pista: En los Ejercicios 29-32, rodear el triángulo con un rectángulo, como los que se muestran en los Ejercicios 25-28.

29. Encuentra el área del triángulo con vértices en A (−4, −1), B (4, −2) y C (1, 3).

30. Encuentra el área del triángulo con vértices en A (−4, 2), B (3, 0) y C (0, 4).

31. Encuentra el área del triángulo con vértices en A (−3, 1), B (3, −3) y C (1, 4).

32. Encuentra el área del triángulo con vértices en A (1, 2), B (3, 0) y C (2, 4).

RESPUESTAS

1. (1, 4)

3. (4, 1)

5. (−3, −1)

7. (−1, 1)

9. 2 unidades cuadradas

11. 20 unidades cuadradas

13. 16 unidades

15. 10 unidades

17. 2 unidades cuadradas

19. 1 unidades cuadradas

21. $\sqrt{18}$

23. $\sqrt{13}$

25. 6

27. 7

29. $\frac{37}{2}$

31. 17

Search

Text Color

Text Size

Margin Size

Font Type