1.1: Introducción a los números enteros (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114221

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Objetivos de aprendizaje

Identificar números de conteo y números enteros
Números enteros del modelo
Identificar el valor positorio de un dígito
Usar el valor positorio para nombrar números enteros
Usar el valor positorio para escribir números enteros
Redondear números enteros

Identificar números de conteo y números enteros

Aprender álgebra es similar a aprender un idioma. Empiezas con un vocabulario básico y luego le agregas a medida que avanzas. Necesitas practicar a menudo hasta que el vocabulario se vuelva fácil para ti. Cuanto más uses el vocabulario, más familiar se vuelve.

El álgebra utiliza números y símbolos para representar palabras e ideas. Veamos primero los números. Los números más básicos utilizados en álgebra son los que usamos para contar objetos:$1, 2, 3, 4, 5, …$ y así sucesivamente. A estos se les llama los números de conteo. A la notación “...” se le llama elipsis, que es otra forma de mostrar “y así sucesivamente”, o que el patrón continúe sin cesar. Los números de conteo también se llaman números naturales.

Definición: Contar números

Los números de conteo comienzan con$1$ y continúan.

$1, 2, 3, 4, 5 \ldots $

El conteo de números y números enteros se puede visualizar en una línea numérica como se muestra en la Figura$\PageIndex{1}$.

$Una imagen de una línea numérica de 0 a 6 en incrementos de uno. Una flecha por encima de la recta numérica apuntando a la derecha con la etiqueta “más grande”. Una flecha apuntando a la izquierda con la etiqueta “más pequeña”.$

Figura$\PageIndex{1}$: Los números en la recta numérica aumentan de izquierda a derecha y disminuyen de derecha a izquierda.

El punto etiquetado$0$ se llama origen. Los puntos están igualmente espaciados a la derecha de 0 y etiquetados con los números de conteo. Cuando un número se empareja con un punto, se llama la coordenada del punto.

El descubrimiento del número cero fue un gran paso en la historia de las matemáticas. Incluir cero con los números de conteo da un nuevo conjunto de números llamados números enteros.

Definición: Números enteros

Los números enteros son los números de conteo y cero.

$0, 1, 2, 3, 4, 5 \ldots$

Nos detuvimos$5$ al enumerar los primeros números de conteo y números enteros. Podríamos haber escrito más números si fueran necesarios para dejar claros los patrones.

Ejemplo$\PageIndex{1}$: Number Identification

¿Cuáles de las siguientes son

contar números
números enteros

\[0, \dfrac{1}{4}, 3, 5.2, 15, 105 \nonumber\]

Solución

Los números de conteo comienzan en$1$, por lo que no$0$ es un número de conteo. Los números$3$,$15$, y$105$ están todos contando números.
Los números enteros están contando números y$0$. Los números$0, 3, 15,$ y$105$ son números enteros. Los números$\dfrac{1}{4}$ y no$5.2$ están contando números ni números enteros. Discutiremos estos números más adelante.

Ejercicio$\PageIndex{1}$

¿Cuáles de las siguientes son

números enteros

\[0, \dfrac{2}{3}, 2, 9, 11.8, 241, 376 \nonumber \]

Contestar a: $2, 9, 241, 376$

Respuesta b: $0, 2, 9, 241, 376$

Ejercicio$\PageIndex{2}$

¿Cuáles de las siguientes son

contar números
números enteros

\[0, \dfrac{5}{3}, 7, 8.8, 13, 201 \nonumber \]

Contestar a: $7, 13, 201$

Respuesta b: $0, 7, 13, 201$

Números enteros del modelo

Nuestro sistema numérico se llama sistema de valor posicionar porque el valor de un dígito depende de su posición, o lugar, en un número. El número$537$ tiene un valor diferente al número$735$. A pesar de que usan los mismos dígitos, su valor es diferente debido a la diferente ubicación del$3$ y el$7$ y el$5$.

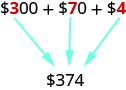
El dinero nos da un modelo familiar de valor posiciona. Supongamos que una billetera contiene tres$$100$$$10$ billetes, siete billetes y cuatro$$1$ billetes. Los montos se resumen en la Figura$\PageIndex{2}$. ¿Cuánto dinero hay en la cartera?

$Una imagen de tres pilas de moneda estadounidense. La primera pila de izquierda a derecha es una pila de 3 billetes de $100, con etiqueta “Tres billetes de $100, 3 veces $100 equivale a $300”. La segunda pila de izquierda a derecha es una pila de 7 billetes de $10, con etiqueta “Siete billetes de $10, 7 veces $10 equivale a $70”. La tercera pila de izquierda a derecha es una pila de 4 billetes de $1, con la etiqueta “Cuatro billetes de $1, 4 veces $1 equivale a $4”.$

Figura$\PageIndex{2}$

Encuentra el valor total de cada tipo de factura, y luego agrega para encontrar el total. El monedero contiene$$374$.

$Una imagen de “$300 + $70 +$4” donde el “3” en “$300”, el “7” en “$70” y el “4” en “$4” están todos en rojo en lugar de negro como el resto de la expresión. Debajo de esta expresión se encuentra el valor “$374”. Una flecha apunta del rojo “3” en la expresión al “3” en “$374”, una flecha apunta al rojo “7” en la expresión al “7” en “$374”, y una flecha apunta desde el rojo “4” en la expresión al “4” en “$374”.$

$10$Los bloques base proporcionan otra forma de modelar el valor positorio, como se muestra en la Figura$\PageIndex{3}$. Los bloques se pueden utilizar para representar cientos, decenas y unos. Observe que la varilla de$10$ las decenas está compuesta por unas, y la escuadra de cientos está hecha de$10$ decenas, o$100$ unas.

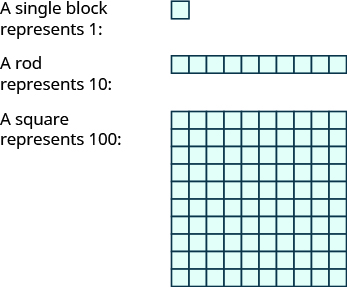
$Una imagen con tres elementos. El primer ítem es un solo bloque con la etiqueta “Un solo bloque representa 1”. El segundo ítem es una varilla horizontal que consta de 10 bloques, con la etiqueta “Una varilla representa 10”. El tercer ítem es un cuadrado que consta de 100 bloques, con la etiqueta “Un cuadrado representa 100”. El cuadrado mide 10 cuadras de alto y 10 cuadras de ancho.$

Figura$\PageIndex{3}$

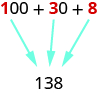
La figura$\PageIndex{4}$ muestra el número$138$ modelado con$10$ bloques base.

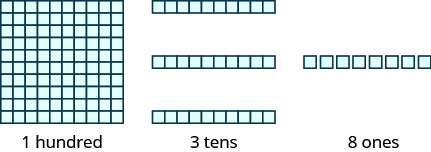
$Una imagen que consta de tres elementos. El primer ítem es un cuadrado de 100 bloques, 10 bloques de ancho y 10 bloques de alto, con la etiqueta “cien”. El segundo ítem es de 3 varillas horizontales que contienen 10 bloques cada una, con la etiqueta “3 decenas”. El tercer ítem es de 8 bloques individuales con la etiqueta “8 unos”.$

Figura$\PageIndex{4}$: Utilizamos notación de valor positorio para mostrar el valor del número 138.

$Una imagen de “100 + 30 +8” donde el “1” en “100”, el “3” en “30” y el “8” están todos en rojo en lugar de negro como el resto de la expresión. Debajo de esta expresión se encuentra el valor “138”. Una flecha apunta del rojo “1” en la expresión al “1” en “138”, una flecha apunta al rojo “3” en la expresión al “3” en “138”, y una flecha apunta desde el rojo “8” en la expresión al “8” en 138.$

Dígito	Valor posiblar	Número	Valor	Valor total
1	cientos	1	100	100
3	decenas	3	10	30
8	unos	8	1	+8
			Suma =	138

Ejemplo$\PageIndex{2}$: place value notation

Utilice la notación de valor posicionar para encontrar el valor del número modelado por los$10$ bloques base mostrados.

$Una imagen que consta de tres elementos. El primer ítem es de dos cuadrados de 100 bloques cada uno, 10 bloques de ancho y 10 bloques de alto. El segundo elemento es una varilla horizontal que contiene 10 bloques. El tercer ítem es de 5 bloques individuales.$

Figura$\PageIndex{5}$

Solución

Hay$2$ cientos de plazas, que es$200$.

Hay$1$ decenas de varilla, que es$10$.

Hay$5$ unos bloques, que es$5$.

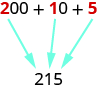
$Una imagen de “200 + 10 + 5” donde el “2” en “200”, el “1” en “10”, y el “5” están todos en rojo en lugar de negro como el resto de la expresión. Debajo de esta expresión se encuentra el valor “215”. Una flecha apunta del rojo “2” en la expresión al “2” en “215”, una flecha apunta al rojo “1” en la expresión al “1” en “215”, y una flecha apunta desde el rojo “5” en la expresión al “5” en 215.$

Dígito	Valor posiblar	Número	Valor	Valor total
2	cientos	2	100	200
1	decenas	1	10	10
5	unos	5	1	+5
				215

Los$10$ bloques base modelan el número$215$.

Ejercicio$\PageIndex{3}$

Utilice la notación de valor posicionar para encontrar el valor del número modelado por los$10$ bloques base mostrados.

$Una imagen que consta de tres elementos. El primer elemento es un cuadrado de 100, 10 bloques de ancho y 10 bloques de alto. El segundo ítem es de 7 barras horizontales que contienen 10 bloques cada una. El tercer ítem es de 6 bloques individuales.$

Figura$\PageIndex{6}$

Contestar: $176$

Ejercicio$\PageIndex{4}$

Utilice la notación de valor posicionar para encontrar el valor del número modelado por los$10$ bloques base mostrados.

$Una imagen que consta de tres elementos. El primer ítem es de dos cuadrados de 100 bloques cada uno, 10 bloques de ancho y 10 bloques de alto. El segundo elemento es de tres barras horizontales que contienen 10 bloques cada una. El tercer ítem es de 7 bloques individuales.$

Figura$\PageIndex{7}$

Contestar: $237$

Identificar el valor positorio de un dígito

Al mirar el dinero y los bloques base-10, vimos que cada lugar en un número tiene un valor diferente. Un gráfico de valores posicionales es una forma útil de resumir esta información. Los valores posicionales se separan en grupos de tres, llamados periodos. Los periodos son unos, miles, millones, miles de millones, billones, y así sucesivamente. En un número escrito, las comas separan los periodos.

Al igual que con los$10$ bloques base, donde el valor de la varilla de decenas es diez veces el valor del bloque unos y el valor de los cientos cuadrados es diez veces la varilla de decenas, el valor de cada lugar en la tabla de valores posicionales es diez veces el valor del lugar a la derecha de la misma.

La figura$\PageIndex{8}$ muestra cómo$5,278,194$ se escribe el número en un gráfico de valores posicionales.

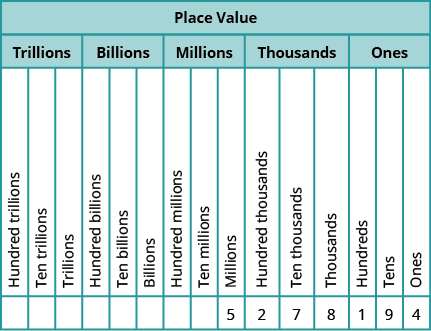
$Un gráfico titulado 'Valor posible' con quince columnas y 4 filas, con las columnas divididas en cinco grupos de tres. La fila de cabecera muestra Trillones, Miles de millones, Millones, Miles y Unos. La siguiente fila tiene los valores 'Cien trillones', 'Diez trillones', 'billones', 'cien mil millones', 'diez mil millones', 'mil millones', 'cien millones', 'diez millones', 'millones', 'cien miles', 'diez miles', 'miles', 'cientos', 'decenas', y 'unos'. Los primeros 8 valores de la siguiente fila están en blanco. A partir de la novena columna, los valores son '5', '2', '7', '8', '1', '9' y '4'.$

Figura$\PageIndex{8}$

El dígito$5$ está en el lugar de millones. Su valor es$5,000,000$.
El dígito$2$ está en el lugar de los cien miles. Su valor es$200,000$.
El dígito$7$ está en el lugar de los diez miles. Su valor es$70,000$.
El dígito$8$ está en el lugar de miles. Su valor es$8,000$.
El dígito$1$ está en el lugar de los cientos. Su valor es$100$.
El dígito$9$ está en el lugar de las decenas. Su valor es$90$.
El dígito$4$ está en el lugar de unos. Su valor es$4$.

Ejemplo$\PageIndex{3}$: place value

En el número$63,407,218$; encuentra el valor posicionar de cada uno de los siguientes dígitos:

Solución

Escriba el número en un gráfico de valores posicionales, comenzando por la derecha.

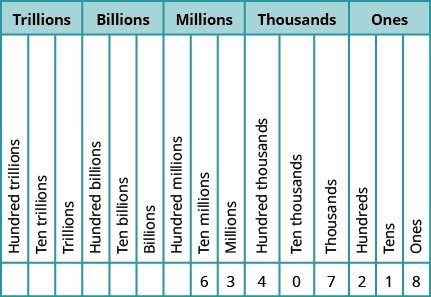
$Una figura titulada “Valores posicionales” con quince columnas y 2 filas, con las columnas divididas en cinco grupos de tres. La primera fila tiene los valores “Cien billones”, “Diez billones”, “billones”, “cien billones”, “diez mil millones”, “mil millones”, “cien millones”, “diez millones”, “millones”, “cien tuosandos”, “diez miles”, “miles”, “cientos”, “decenas”, y “unos”. Los primeros 7 valores de la segunda fila están en blanco. A partir de la octava columna, los valores son “6”, “3”, “4”, “0”, “7”, “2”, “1” y “8”. El primer grupo está etiquetado como “billones” y contiene los valores de la primera fila de “Cien billones”, “diez billones” y “billones”. El segundo grupo está etiquetado como “miles de millones” y contiene los valores de la primera fila de “Cien miles de millones”, “diez mil millones” y “miles de millones”. El tercer grupo está etiquetado como “millones” y contiene los valores de la primera fila de “Cien millones”, “diez millones” y “millones”. El cuarto grupo está etiquetado como “miles” y contiene los valores de la primera fila de “Cien miles”, “diez miles” y “miles”. El quinto grupo está etiquetado como “unos” y contiene los valores de la primera fila de “Cientos”, “decenas” y “unos”.$

Figura$\PageIndex{9}$

El$7$ está en el lugar de miles.
El$0$ está en el lugar de los diez miles.
El$1$ está en el lugar de las decenas.
El$6$ está en el lugar de los diez millones.
El$3$ está en el lugar de los millones.

Ejercicio$\PageIndex{5}$

Para cada número, encuentre el valor posicionar de los dígitos enumerados:$27,493,615$

$2$
$1$
$4$
$7$
$5$

Contestar a: $2$

Respuesta b: $1$

Contestar c: $4$

Respuesta d: $7$

Respuesta e: $5$

Ejercicio$\PageIndex{6}$

Para cada número, encuentre el valor posicionar de los dígitos enumerados:$519,711,641,328$

$9$
$4$
$2$
$6$
$7$

Contestar a: miles de millones

Respuesta b: diez miles

Contestar c: decenas

Respuesta d: cien miles

Respuesta e: cien millones

Usar el valor positorio para nombrar números enteros

Cuando escribes un cheque, escribes el número en palabras así como en cifras. Para escribir un número en palabras, escriba el número en cada periodo seguido del nombre del periodo sin la 's' al final. Comience con el dígito de la izquierda, que tiene el mayor valor posicionar. Las comas separan los puntos, así que dondequiera que haya una coma en el número, escriba una coma entre las palabras. El periodo unos, que tiene el menor valor positorio, no se nombra.

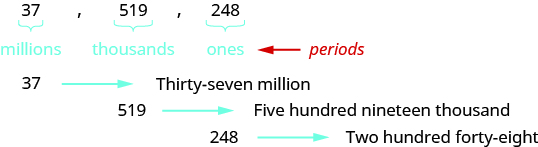
$Una imagen con tres valores separados por comas. El primer valor es “37” y tiene la etiqueta “millones”. El segundo valor es “519” y tiene la etiqueta miles. El tercer valor es “248” y tiene los de etiqueta. Debajo, el valor “37” tiene una flecha que apunta a “Treinta y siete millones”, el valor “519” tiene una flecha que apunta a “Quinientos diecinueve mil”, y el valor “248” tiene una flecha que apunta a “Doscientos cuarenta y ocho”.$

Entonces el número$37,519,248$ está escrito treinta y siete millones, quinientos diecinueve mil, doscientos cuarenta y ocho. Observe que la palabra y no se usa al nombrar un número entero.

Cómo: Nombrar un número entero en palabras.

Paso 1. Comenzando por el dígito de la izquierda, nombra el número en cada periodo, seguido del nombre del período. No incluya el nombre del período para los.

Paso 2. Use comas en el número para separar los puntos.

Ejemplo$\PageIndex{4}$: name whole numbers

Nombra el número$8,165,432,098,710$ en palabras.

Solución

Comience con el dígito más a la izquierda, que es$8$. Está en el lugar de los billones.	ocho billones
El siguiente periodo a la derecha es de miles de millones.	ciento sesenta y cinco mil millones
El siguiente periodo a la derecha es de millones.	cuatrocientos treinta y dos millones
El siguiente periodo a la derecha es de miles.	noventa y ocho mil
El periodo más a la derecha muestra los unos.	setecientos diez

$Una imagen con cinco valores separados por comas. El primer valor es “8” y tiene la etiqueta “billones”. El segundo valor es “165” y tiene la etiqueta “biliones”. El tercer valor es “432” y tiene la etiqueta “millones”. El cuarto valor es “098” y tiene la etiqueta “miles”. El quinto valor es “710” y tiene la etiqueta “unos”. Debajo, el valor “8” tiene una flecha que apunta a “Ocho billones”, el valor “165” tiene una flecha que apunta a “Ciento sesenta y cinco mil millones”, el valor “432” tiene una flecha que apunta a “Cuatrocientos treinta y dos millones”, el valor “098” tiene una flecha que apunta a “Noventa y ocho mil”, y el valor “710” tiene una flecha apuntando a “setecientos diez”.$

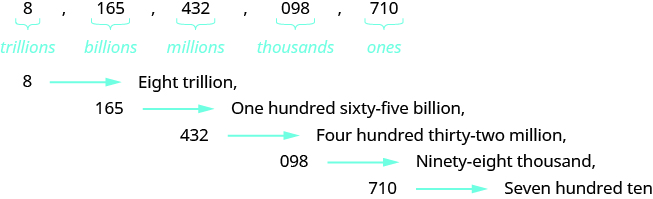
Juntando todas las palabras, escribimos$8,165,432,098,710$ como ocho billones, ciento sesenta y cinco mil, cuatrocientos treinta y dos millones, noventa y ocho mil, setecientos diez.

Ejercicio$\PageIndex{7}$

Nombra cada número en palabras:$9,258,137,904,061$

Contestar: nueve billones, doscientos cincuenta y ocho mil millones, ciento treinta y siete millones, novecientos cuatro mil, sesenta y uno

Ejercicio$\PageIndex{8}$

Nombra cada número en palabras:$17,864,325,619,004$

Contestar: diecisiete billones, ochocientos sesenta y cuatro mil millones, trescientos veinticinco millones, seiscientos diecinueve mil, cuatro

Ejemplo$\PageIndex{5}$: name whole numbers

Un estudiante realizó una investigación y encontró que el número de usuarios de teléfonos móviles en Estados Unidos durante un mes en 2014 fue$327,577,529$. Nombra ese número en palabras.

Solución

Identificar los periodos asociados al número.

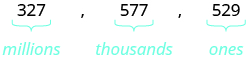
$Una imagen con tres valores separados por comas. El primer valor es “327” y tiene la etiqueta “millones”. El segundo valor es “577” y tiene la etiqueta “miles”. El tercer valor es “529” y tiene la etiqueta “unos”.$

Nombra el número en cada periodo, seguido del nombre del periodo. Poner las comas para separar los periodos.

Periodo de millones: trescientos veintisiete millones

Período de miles: quinientos setenta y siete mil

Periodo unos: quinientos veintinueve

Por lo que el número de usuarios de telefonía móvil en los Estados Unidos durante el mes de abril fue de trescientos veintisiete millones, quinientos setenta y siete mil quinientos veintinueve.

Ejercicio$\PageIndex{9}$

La población en un país es$316,128,839$. Nombra ese número

Contestar: trescientos dieciséis millones, ciento veintiocho mil ochocientos treinta y nueve

Ejercicio$\PageIndex{10}$

Un año son$31,536,000$ segundos. Nombra ese número.

Contestar: treinta y un millón quinientos treinta y seis mil

Usar valor positorio para escribir números enteros

Ahora invertiremos el proceso y escribiremos un número dado en palabras como dígitos.

Cómo: Usar el Valor Positivo para Escribir Números Enteros

Paso 1. Identificar las palabras que indican periodos. (Recuerde que el período de unos nunca se nombra.)

Paso 2. Dibuja tres espacios en blanco para indicar el número de lugares necesarios en cada periodo. Separar los periodos por comas.

Paso 3. Nombra el número en cada periodo y coloca los dígitos en la posición correcta del valor posicionar.

Ejemplo$\PageIndex{6}$: write whole numbers

Escribe los siguientes números usando dígitos.

cincuenta y tres millones cuatrocientos mil setecientos cuarenta y dos
nueve mil millones, doscientos cuarenta y seis millones, setenta y tres mil, ciento ochenta y nueve

Solución

Identificar las palabras que indican periodos.

Salvo el primer periodo, todos los demás periodos deberán tener tres plazas. Dibuja tres espacios en blanco para indicar el número de lugares necesarios en cada periodo. Separar los periodos por comas.

Después escribe los dígitos en cada periodo.

$Una imagen con tres bloques de texto apuntando a valores numéricos. El primer bloque de texto es “cincuenta y tres millones”, tiene la etiqueta “millones”, y apunta al valor 53. El segundo bloque de texto es “cuatrocientos mil”, tiene la etiqueta “miles”, y apunta al valor 401. El tercer bloque de texto es “setecientos cuarenta y dos”, tiene la etiqueta “unos”, y apunta al valor 742.$

Junte los números, incluyendo las comas. El número es$53,401,742$.

Identificar las palabras que indican periodos.

Después escribe los dígitos en cada periodo.

$Una imagen con cuatro bloques de texto apuntando a valores numéricos. El primer bloque de texto es “nueve mil millones”, tiene la etiqueta “miles de millones”, y apunta al valor 9. El segundo bloque de texto es “doscientos cuarenta y seis millones”, tiene la etiqueta “millones”, y apunta al valor 246. El tercer bloque de texto es “setenta y tres mil”, tiene la etiqueta “miles”, y apunta al valor 742. El cuarto bloque de texto es “ciento ochenta y nueve”, tiene la etiqueta “unos”, y apunta al valor 189.$

El número es$9,246,073,189.$

Observe que en la parte (b), se necesitaba un cero como colocador en el lugar de los cien miles. Asegúrese de escribir ceros según sea necesario para asegurarse de que cada periodo, excepto posiblemente el primero, tenga tres lugares.

Ejercicio$\PageIndex{11}$

Escribe cada número en forma estándar:

cincuenta y tres millones ochocientos nueve mil cincuenta y uno

Contestar: $53,809,051$

Ejercicio$\PageIndex{12}$

Escribe cada número en forma estándar:

dos mil millones, veintidós millones, setecientos catorce mil cuatrocientos sesenta y seis

Contestar: $2,022,714,466$

Ejemplo$\PageIndex{7}$: write standard form

Un presupuesto estatal era de alrededor de$$77$ mil millones. Escribir el presupuesto en forma estándar.

Solución

Identificar los periodos. En este caso, sólo se dan dos dígitos y están en el periodo de miles de millones. Para escribir el número entero, escribir ceros para todos los demás periodos.

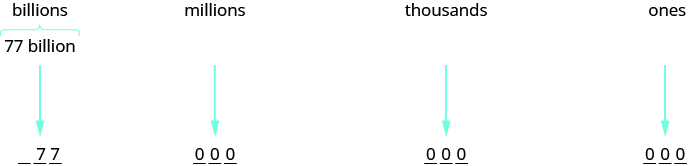
$Una imagen con cuatro bloques de texto apuntando a valores numéricos. El primer bloque de texto es “77 mil millones”, tiene la etiqueta “miles de millones”, y apunta al valor “77”. El segundo bloque de texto es nulo, tiene la etiqueta “millones”, y apunta al valor “000”. El tercer bloque de texto es nulo, tiene la etiqueta “miles”, y apunta al valor “000”. El cuarto bloque de texto es nulo, tiene la etiqueta “unos”, y apunta al valor “000”.$

Entonces el presupuesto estaba a punto$$77,000,000,000$.

Ejercicio$\PageIndex{13}$

Escribe cada número en forma estándar:

La distancia más cercana de la Tierra a Marte es de aproximadamente$34$ un millón de millas.

Contestar: $34,000,000\: miles$

Ejercicio$\PageIndex{14}$

Escribe cada número en forma estándar:

El peso total de un portaaviones es de$204$ millones de libras.

Contestar: $204,000,000\: pounds$

Colaboradores y Atribuciones

Template:ContribElementaryAlgebraOpenStax

Search

Definición: Contar números

Definición: Números enteros

Ejemplo\(\PageIndex{1}\): Number Identification

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{2}\): place value notation

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejemplo\(\PageIndex{3}\): place value

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Cómo: Nombrar un número entero en palabras.

Ejemplo\(\PageIndex{4}\): name whole numbers

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejemplo\(\PageIndex{5}\): name whole numbers

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Cómo: Usar el Valor Positivo para Escribir Números Enteros

Ejemplo\(\PageIndex{6}\): write whole numbers

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejemplo\(\PageIndex{7}\): write standard form

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)