Saltar al contenido principal
LibreTexts Español

2.E: Introducción al Lenguaje del Álgebra (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114259

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    2.1 - Utilizar el lenguaje del álgebra

    Usar variables y símbolos algebraicos

    En los siguientes ejercicios, traduzca del álgebra al inglés.

    1. 3 • 8
    2. 12 − x
    3. 24 ÷ 6
    4. 9 + 2a
    5. 50 ≥ 47
    6. 3 años < 15
    7. n + 4 = 13
    8. 32 − k = 7

    Identificar expresiones y ecuaciones

    En los siguientes ejercicios, determine si cada uno es una expresión o ecuación.

    1. 5 + u = 84
    2. 36 − 6s
    3. 4 años − 11
    4. 10x = 120

    Simplificar expresiones con exponentes

    En los siguientes ejercicios, escribe en forma exponencial.

    1. 2 • 2 • 2
    2. a • a • a • a • a
    3. x • x • x • x • x
    4. 10 • 10 • 10

    En los siguientes ejercicios, escribe en forma expandida.

    1. 8 4
    2. 3 6
    3. y 5
    4. n 4

    En los siguientes ejercicios, simplifique cada expresión.

    1. 3 4
    2. 10 6
    3. 2 7
    4. 4 3

    Simplificar expresiones usando el orden de las operaciones

    En los siguientes ejercicios, simplifique.

    1. 10 + 2 • 5
    2. (10 + 2) • 5
    3. (30 + 6) ÷ 2
    4. 30 + 6 ÷ 2
    5. 7 2 + 5 2
    6. (7 + 5) 2
    7. 4 + 3 (10 − 1)
    8. (4 + 3) (10 − 1)

    2.2 - Evaluar, simplificar y traducir expresiones

    Evaluar una expresión

    En los siguientes ejercicios, evalúe las siguientes expresiones.

    1. 9x − 5 cuando x = 7
    2. y 3 cuando y = 5
    3. 3a − 4b cuando a = 10, b = 1
    4. bh cuando b = 7, h = 8

    Identificar términos, coeficientes y términos similares

    En los siguientes ejercicios, identificar los términos en cada expresión.

    1. 12n 2 + 3n + 1
    2. 4x 3 + 11x + 3

    En los siguientes ejercicios, identificar el coeficiente de cada término.

    1. 6y
    2. 13x 2

    En los siguientes ejercicios, identifique los términos similares.

    1. 5x 2, 3, 5y 2, 3x, x, 4
    2. 8, 8r 2, 8r, 3r, r 2, 3s

    Simplificar expresiones combinando términos similares

    En los siguientes ejercicios, simplifique las siguientes expresiones combinando términos similares.

    1. 15a + 9a
    2. 12 años + 3 años + y
    3. 4x + 7x + 3x
    4. 6 + 5c + 3
    5. 8n + 2 + 4n + 9
    6. 19p + 5 + 4p − 1 + 3p
    7. 7y 2 + 2y + 11 + 3y 2 − 8
    8. 13x 2 − x + 6 + 5x 2 + 9x

    Traducir frases en inglés a expresiones algebraicas

    En los siguientes ejercicios, traduzca las siguientes frases en expresiones algebraicas.

    1. la diferencia de x y 6
    2. la suma de 10 y dos veces por
    3. el producto de 3n y 9
    4. el cociente de s y 4
    5. 5 veces la suma de y y 1
    6. 10 menos que el producto de 5 y z
    7. Jack compró un sándwich y un café. El costo del sándwich fue de $3 más que el costo del café. Llame al costo del café c. Escriba una expresión para el costo del sándwich.
    8. El número de libros de poesía en la estantería de Brianna es 5 menos del doble del número de novelas. Llamar al número de novelas n. Escribe una expresión para el número de libros de poesía.

    2.3 - Resolver ecuaciones usando las propiedades de resta y suma de la igualdad

    Determinar si un número es una solución de una ecuación

    En los siguientes ejercicios, determine si cada número es una solución a la ecuación.

    1. y + 16 = 40
      1. 24
      2. 56
    2. d − 6 = 21
      1. 15
      2. 27
    3. 4n + 12 = 36
      1. 6
      2. 12
    4. 20q − 10 = 70
      1. 3
      2. 4
    5. 15x − 5 = 10x + 45
      1. 2
      2. 10
    6. 22p − 6 = 18p + 86
      1. 4
      2. 23

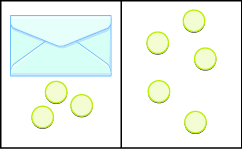
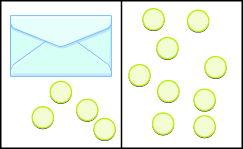
    Modelar la Propiedad de Sustracción de Igualdad

    En los siguientes ejercicios, escriba la ecuación modelada por los sobres y los contadores y luego resuelva la ecuación usando la propiedad de resta de igualdad

    1. Esta imagen se divide en dos partes: la primera parte muestra un sobre y 3 contadores azules y la siguiente, la segunda parte muestra cinco contadores.
    2. Esta imagen se divide en dos partes: la primera parte muestra un sobre y 4 contadores azules y junto a ella, la segunda parte muestra 9 contadores.

    Resolver ecuaciones usando la Propiedad de Sustracción de Igualdad

    En los siguientes ejercicios, resuelve cada ecuación usando la propiedad de resta de igualdad.

    1. c + 8 = 14
    2. v + 8 = 150
    3. 23 = x + 12
    4. 376 = n + 265

    Resolver ecuaciones usando la propiedad de suma de igualdad

    En los siguientes ejercicios, resuelve cada ecuación usando la propiedad de suma de igualdad.

    1. y − 7 = 16
    2. k − 42 = 113
    3. 19 = p − 15
    4. 501 = u − 399

    Traducir frases en inglés a ecuaciones algebraicas

    En los siguientes ejercicios, traduzca cada oración en inglés a una ecuación algebraica.

    1. La suma de 7 y 33 es igual a 40.
    2. La diferencia de 15 y 3 es igual a 12.
    3. El producto de 4 y 8 es igual a 32.
    4. El cociente de 63 y 9 es igual a 7.
    5. Dos veces la diferencia de n y 3 da 76.
    6. La suma de cinco veces y y 4 es 89.

    Traducir a una ecuación y resolver

    En los siguientes ejercicios, traducir cada oración en inglés a una ecuación algebraica y luego resolverla.

    1. Ocho más que x es igual a 35.
    2. 21 menos que a es 11.
    3. La diferencia de q y 18 es 57.
    4. La suma de m y 125 es 240.

    Práctica Mixta

    En los siguientes ejercicios, resuelve cada ecuación.

    1. h − 15 = 27
    2. k − 11 = 34
    3. z + 52 = 85
    4. x + 93 = 114
    5. 27 = q + 19
    6. 38 = p + 19
    7. 31 = v − 25
    8. 38 = u − 16

    2.4 - Encuentra múltiplos y factores

    Identificar múltiplos de números

    En los siguientes ejercicios, enumere todos los múltiplos menores a 50 para cada uno de los siguientes.

    1. 3
    2. 2
    3. 8
    4. 10

    Usar pruebas comunes de divisibilidad

    En los siguientes ejercicios, utilizando las pruebas de divisibilidad, determinar si cada número es divisible por 2, por 3, por 5, por 6 y por 10.

    1. 96
    2. 250
    3. 420
    4. 625

    Encuentra todos los factores de un número

    En los siguientes ejercicios, encuentra todos los factores de cada número.

    1. 30
    2. 70
    3. 180
    4. 378

    Identificar números primos y compuestos

    En los siguientes ejercicios, identifique cada número como primo o compuesto.

    1. 19
    2. 51
    3. 121

    2.5 - Factorización de Prime y el Múltiple Mínimo Común

    Encuentre la factorización principal de un número compuesto

    En los siguientes ejercicios, encuentra la factorización prima de cada número.

    1. 84
    2. 165
    3. 350
    4. 572

    Encuentra el múltiplo menos común de dos números

    En los siguientes ejercicios, encuentra el múltiplo menos común de cada par de números.

    1. 9, 15
    2. 12, 20
    3. 25, 35
    4. 18, 40

    Matemáticas cotidianas

    1. Describe cómo has usado dos temas del capítulo El lenguaje del álgebra en tu vida fuera de tu clase de matemáticas durante el último mes.

    PRUEBA DE PRÁCTICA

    En los siguientes ejercicios, traduzca de una ecuación algebraica a frases en inglés.

    1. 6 • 4
    2. 15 − x

    En los siguientes ejercicios, identificar cada uno como una expresión o ecuación.

    1. 5 • 8 + 10
    2. x + 6 = 9
    3. 3 • 11 = 33
    4. (a) Escribir n • n • n • n • n • n en forma exponencial. (b) Escribir 3 5 en forma ampliada y luego simplificar.

    En los siguientes ejercicios, simplifique, utilizando el orden de las operaciones.

    1. 4 + 3 • 5
    2. (8 + 1) • 4
    3. 1 + 6 (3 − 1)
    4. (8 + 4) ÷ 3 + 1
    5. (1 + 4) 2
    6. 5 [2 + 7 (9 − 8)]

    En los siguientes ejercicios, evalúe cada expresión.

    1. 8x − 3 cuando x = 4
    2. y 3 cuando y = 5
    3. 6a − 2b cuando a = 5, b = 7
    4. hw cuando h = 12, w = 3
    5. Simplifica combinando términos similares.
      1. 6x + 8x
      2. 9m + 10 + m + 3

    En los siguientes ejercicios, traducir cada frase en una expresión algebraica.

    1. 5 más que x
    2. el cociente de 12 e y
    3. tres veces la diferencia de a y b
    4. Caroline tiene 3 aretes menos en su oreja izquierda que en su oreja derecha. Llama al número de aretes en su oreja derecha, r. escribe una expresión para el número de aretes en su oreja izquierda.

    En los siguientes ejercicios, resuelve cada ecuación.

    1. n − 6 = 25
    2. x + 58 = 71

    En los siguientes ejercicios, traducir cada oración en inglés a una ecuación algebraica y luego resolverla.

    1. 15 menos que y es 32.
    2. la suma de a y 129 es 164.
    3. Enumere todos los múltiplos de 4, que son menores a 50.
    4. Encuentra todos los factores de 90.
    5. Encuentra la factorización prima de 1080.
    6. Encuentra el MCM (Mínimo Común Múltiple) de 24 y 40.

    Colaboradores y Atribuciones

    This page titled 2.E: Introducción al Lenguaje del Álgebra (Ejercicios) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.