9.4: Propiedades de Uso de Ángulos, Triángulos y Teorema de Pitágoras (Parte 1)
- Page ID
- 114165
- Usar las propiedades de los ángulos
- Utilizar las propiedades de los triángulos
- Usa el Teorema de Pitágoras
Antes de comenzar, toma este cuestionario de preparación.
- Resolver: x + 3 + 6 = 11. Si te perdiste este problema, revisa el Ejemplo 8.1.6.
- Resolver:\(\dfrac{a}{45} = \dfrac{4}{3}\). Si te perdiste este problema, revisa el Ejemplo 6.5.3.
- Simplificar:\(\sqrt{36 + 64}\). Si te perdiste este problema, revisa el Ejemplo 5.12.4.
En lo que va de este capítulo, nos hemos centrado en resolver problemas de palabras, que son similares a muchas aplicaciones del álgebra en el mundo real. En las siguientes secciones, aplicaremos nuestras estrategias de resolución de problemas a algunos problemas de geometría comunes.
Usar las propiedades de los ángulos
¿Conoces la frase 'haz un 180'? Significa girar para que te mires en sentido contrario. Viene del hecho de que la medida de un ángulo que hace una línea recta es de 180 grados. Ver Figura\(\PageIndex{1}\).
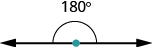
Figura\(\PageIndex{1}\)
Un ángulo está formado por dos rayos que comparten un punto final común. Cada rayo se llama lado del ángulo y el punto final común se llama vértice. Un ángulo es nombrado por su vértice. En la Figura\(\PageIndex{2}\), A es el ángulo con vértice en el punto A. La medida de A está escrita m A.
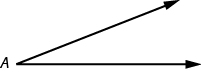
Figura\(\PageIndex{2}\) - A es el ángulo con vértice en el punto A.
Medimos ángulos en grados, y usamos el símbolo° para representar grados. Utilizamos la abreviatura m para la medida de un ángulo. Entonces, si A es 27°, escribiríamos m A = 27.
Si la suma de las medidas de dos ángulos es de 180°, entonces se les llama ángulos suplementarios. En la Figura\(\PageIndex{3}\), cada par de ángulos es suplementario porque sus medidas se suman a 180°. Cada ángulo es el suplemento del otro.
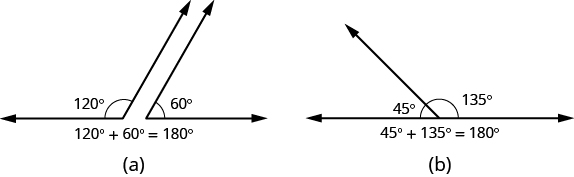
Figura\(\PageIndex{3}\) - La suma de las medidas de los ángulos suplementarios es de 180°.
Si la suma de las medidas de dos ángulos es 90°, entonces los ángulos son ángulos complementarios. En la Figura\(\PageIndex{4}\), cada par de ángulos es complementario, debido a que sus medidas suman 90°. Cada ángulo es el complemento del otro.
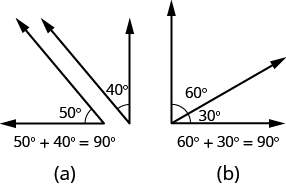
Figura\(\PageIndex{4}\) - La suma de las medidas de los ángulos complementarios es de 90°.
Si la suma de las medidas de dos ángulos es 180°, entonces los ángulos son suplementarios.
Si A y B son suplementarios, entonces ma + mb = 180°.
Si la suma de las medidas de dos ángulos es 90°, entonces los ángulos son complementarios.
Si A y B son complementarios, entonces Ma + Mb = 90°.
En esta sección y en la siguiente, se le presentarán algunas fórmulas geométricas comunes. Adaptaremos nuestra Estrategia de Resolución de Problemas para Aplicaciones de Geometría. La fórmula de geometría nombrará las variables y nos dará la ecuación a resolver.
Además, dado que todas estas aplicaciones implicarán formas geométricas, será útil dibujar una figura y luego etiquetarla con la información del problema. Incluiremos este paso en la Estrategia de Resolución de Problemas para Aplicaciones Geométricas.
Paso 1. Lee el problema y asegúrate de entender todas las palabras e ideas. Dibuja una figura y etiquétela con la información dada.
Paso 2. Identifica lo que buscas
Paso 3. Nombra lo que buscas y elige una variable para representarlo.
Paso 4. Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
Paso 5. Resolver la ecuación usando buenas técnicas de álgebra.
Paso 6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
Paso 7. Contesta la pregunta con una oración completa.
El siguiente ejemplo mostrará cómo se puede utilizar la Estrategia de Resolución de Problemas para Aplicaciones de Geometría para responder preguntas sobre ángulos suplementarios y complementarios.
Un ángulo mide 40°. Encontrar (a) su suplemento, y (b) su complemento.
Solución
(a)
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 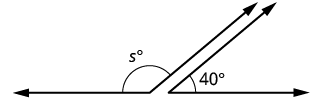 |
| Paso 2. Identifica lo que buscas. | el suplemento de un 40° |
| Paso 3. Nombre. Elija una variable para representarla. | let s = la medida del suplemento |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación y sustituirla en la información dada. | $$m\ ángulo A + m\ ángulo B = 180$$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} s + 40 &= 180\\ s &= 140\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 140 + 40 &\ stackrel {?} {=} 180\\ 180 &= 180\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | El suplemento del ángulo de 40° es 140°. |
b)
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 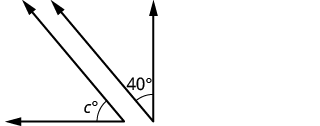 |
| Paso 2. Identifica lo que buscas. | el complemento de un 40° |
| Paso 3. Nombre. Elija una variable para representarla. | let c = la medida del complemento |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación y sustituirla en la información dada. | $$m\ ángulo A + m\ ángulo B = 90$$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} c + 40 &= 90\\ c &= 50\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 50 + 40 &\ stackrel {?} {=} 90\\ 90 &= 90\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | El suplemento del ángulo de 40° es de 50°. |
Un ángulo mide 25°. Encontrar (a) su suplemento, y (b) su complemento.
- Contestar a
-
155°
- Respuesta b
-
65°
Un ángulo mide 77°. Encontrar (a) su suplemento, y (b) su complemento.
- Contestar a
-
103°
- Respuesta b
-
13°
¿Notó que las palabras complementarias y suplementarias están en orden alfabético al igual que 90 y 180 están en orden numérico?
Dos ángulos son suplementarios. El ángulo más grande es 30° más que el ángulo más pequeño. Encuentra la medida de ambos ángulos.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 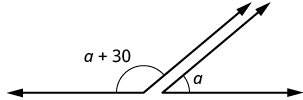 |
| Paso 2. Identifica lo que buscas. | las medidas de ambos ángulos |
| Paso 3. Nombre. Elija una variable para representarla. |
let a = medida del ángulo más pequeño a + 30 = medida del ángulo mayor |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación y sustituirla en la información dada. | $$m\ ángulo A + m\ ángulo B = 180$$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} (a + 30) + a &= 180\\ 2a + 30 &= 180\\ 2a &= 150\\ a &= 75\ cuádruple medida\; de\; menor\; ángulo\\ a &+ 30\ cuádruple medida\; de\; mayor\; ángulo\\ 75 &+ 30\\ &105\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} m\ ángulo A + m\ ángulo B &= 180\\ 75 + 105 &\ stackrel {?} {=} 180\\ 180 &= 180\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | Las medidas de los ángulos son 75° y 105°. |
Dos ángulos son suplementarios. El ángulo más grande es 100° más que el ángulo más pequeño. Encuentra las medidas de ambos ángulos.
- Contestar
-
40°, 140°
Dos ángulos son complementarios. El ángulo más grande es 40° más que el ángulo más pequeño. Encuentra las medidas de ambos ángulos.
- Contestar
-
25°, 65°
Utilizar las propiedades de los triángulos
¿Qué sabes ya de los triángulos? Triángulo tiene tres lados y tres ángulos. Los triángulos son nombrados por sus vértices. El triángulo en la Figura\(\PageIndex{5}\) se llama ΔABC, lee 'triángulo ABC'. Etiquetamos cada lado con una letra minúscula para que coincida con la letra mayúscula del vértice opuesto.
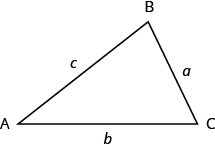
Figura\(\PageIndex{5}\) - ΔABC tiene los vértices A, B y C y los lados a, b y c.
Los tres ángulos de un triángulo están relacionados de una manera especial. La suma de sus medidas es de 180°.
\[m \angle A + m \angle B + m \angle C = 180°\]
Para cualquier ΔABC, la suma de las medidas de los ángulos es de 180°.
\[m \angle A + m \angle B + m \angle C = 180°\]
Las medidas de dos ángulos de un triángulo son 55° y 82°. Encuentra la medida del tercer ángulo.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 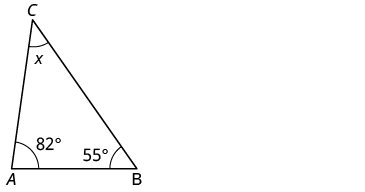 |
| Paso 2. Identifica lo que buscas. | la medida del tercer ángulo en un triángulo |
| Paso 3. Nombre. Elija una variable para representarla. | let x = la medida del ángulo |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación y sustituirla en la información dada. | $$m\ ángulo A + m\ ángulo B + m\ ángulo C = 180$$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} 55 + 82 + x &= 180\\ 137 + x &= 180\\ x &= 43\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 55 + 82 + 43 &\ stackrel {?} {=} 180\\ 180 &= 180\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | La medida del tercer ángulo es de 43 grados. |
Las medidas de dos ángulos de un triángulo son 31° y 128°. Encuentra la medida del tercer ángulo.
- Contestar
-
21°
Un triángulo tiene ángulos de 49° y 75°. Encuentra la medida del tercer ángulo.
- Contestar
-
56°
Triángulos rectos
Algunos triángulos tienen nombres especiales. Vamos a mirar primero el triángulo rectángulo. Un triángulo rectángulo tiene un ángulo de 90°, que a menudo se marca con el símbolo que se muestra en la Figura\(\PageIndex{6}\).
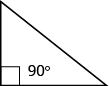
Figura\(\PageIndex{6}\)
Si sabemos que un triángulo es un triángulo rectángulo, sabemos que un ángulo mide 90° por lo que solo necesitamos la medida de uno de los otros ángulos para determinar la medida del tercer ángulo.
Un ángulo de un triángulo rectángulo mide 28°. ¿Cuál es la medida del tercer ángulo?
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 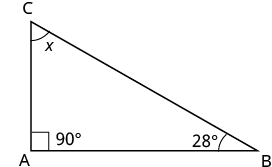 |
| Paso 2. Identifica lo que buscas. | la medida de un ángulo |
| Paso 3. Nombre. Elija una variable para representarla. | let x = la medida del ángulo |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación y sustituirla en la información dada. | $$m\ ángulo A + m\ ángulo B + m\ ángulo C = 180$$ |
| Paso 5. Resuelve la ecuación. | $$\ comenzar {dividir} x + 90 + 28 &= 180\\ x + 118 &= 180\\ x &= 62\ fin {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 180 &\ stackrel {?} {=} 90 + 28 + 62\\ 180 &= 180\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | La medida del tercer ángulo es 62°. |
Un ángulo de un triángulo rectángulo mide 56°. ¿Cuál es la medida del otro ángulo?
- Contestar
-
34°
Un ángulo de un triángulo rectángulo mide 45°. ¿Cuál es la medida del otro ángulo?
- Contestar
-
45°
En los ejemplos hasta ahora, podríamos dibujar una figura y etiquetarla directamente después de leer el problema. En el siguiente ejemplo, tendremos que definir un ángulo en términos de otro. Entonces esperaremos a dibujar la figura hasta que escribamos expresiones para todos los ángulos que estamos buscando.
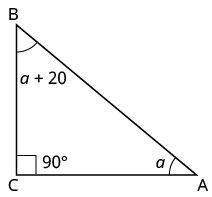
La medida de un ángulo de un triángulo rectángulo es 20° más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | las medidas de los tres ángulos |
| Paso 3. Nombre. Elija una variable para representarla. Ahora dibuja la figura y etiquétela con la información dada. |
Dejar a = 1 st ángulo a + 20 = 2º ángulo 90 = 3º ángulo (el ángulo recto)
|
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación y sustituirla en la información dada. | $$\ comenzar {dividir} m\ ángulo A + m\ ángulo B + m\ ángulo C &= 180\\ a + (a + 20) + 90 &= 180\ final {split} $$ |
| Paso 5. Resuelve la ecuación. | $$\ begin {split} 2a + 110 &= 180\\ 2a &= 70\\ a &= 35\ cuádruple primero\; ángulo\\ a + &20\ cuádruple segundo\; ángulo\\\ textcolor {rojo} {35} + &20\\ &55\ &90\ cuádruple tercer\; ángulo\ final {split} $$ |
| Paso 6. Cheque. | $$\ begin {split} 35 + 55 + 90 &\ stackrel {?} {=} 180\\ 180 &= 180\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta. | Los tres ángulos miden 35°, 55° y 90°. |
La medida de un ángulo de un triángulo rectángulo es 50° más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
- Contestar
-
20°, 70°, 90°
La medida de un ángulo de un triángulo rectángulo es 30° más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
- Contestar
-
30°, 60°, 90°
Triángulos similares
Cuando usamos un mapa para planear un viaje, un boceto para construir una estantería, o un patrón para coser un vestido, estamos trabajando con figuras similares. En geometría, si dos figuras tienen exactamente la misma forma pero diferentes tamaños, decimos que son figuras similares. Uno es un modelo a escala del otro. Los lados correspondientes de las dos figuras tienen la misma relación, y todos sus ángulos correspondientes tienen las mismas medidas.
Los dos triángulos en la Figura\(\PageIndex{7}\) son similares. Cada lado de ΔABC es cuatro veces la longitud del lado correspondiente de ΔXYZ y sus ángulos correspondientes tienen medidas iguales.
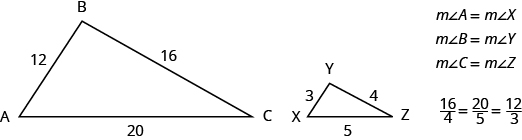
Figura\(\PageIndex{7}\) - ΔABC y ΔXYZ son triángulos similares. Sus lados correspondientes tienen la misma relación y los ángulos correspondientes tienen la misma medida.
Si dos triángulos son similares, entonces sus medidas de ángulo correspondientes son iguales y sus longitudes laterales correspondientes están en la misma proporción.
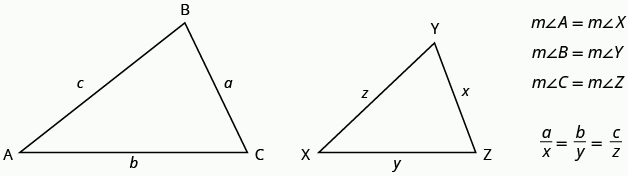
La longitud de un lado de un triángulo puede ser referida por sus extremos, dos vértices del triángulo. Por ejemplo, en ΔABC:
la longitud a también se puede escribir BC
la longitud b también se puede escribir AC
la longitud c también se puede escribir AB
A menudo usaremos esta notación cuando resolvamos triángulos similares porque nos ayudará a emparejar las longitudes laterales correspondientes.
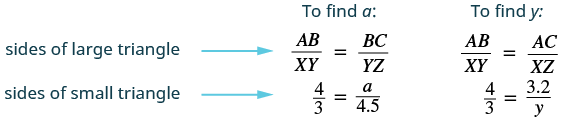
ΔABC y ΔXYZ son triángulos similares. Se muestran las longitudes de dos lados de cada triángulo. Encuentra las longitudes del tercer lado de cada triángulo.
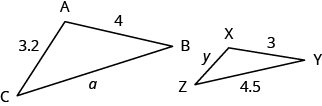
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | Se proporciona la cifra. |
| Paso 2. Identifica lo que buscas. | La longitud de los lados de triángulos similares |
| Paso 3. Nombre. Elija una variable para representarla. | Let a = longitud del tercer lado de ΔABC, y = longitud del tercer lado ΔXYZ |
| Paso 4. Traducir. |
Los triángulos son similares, por lo que los lados correspondientes están en la misma proporción. So$$\ dfrac {AB} {XY} =\ dfrac {BC} {YZ} =\ dfrac {AC} {XZ} $$Ya que el lado AB = 4 corresponde al lado XY = 3, usaremos la relación\(\dfrac{AB}{XY} = \dfrac{4}{3}\) para encontrar los otros lados. Tenga cuidado de hacer coincidir correctamente los lados correspondientes.
|
| Paso 5. Resuelve la ecuación. | $$\ begin {split} 3a &= 4 (4.5)\ qquad\; 4y = 3 (3.2)\\ 3a &= 18\ qquad\ qquad 4y = 9.6\\ a &= 6\ qquad\ qquad\ quad y = 2.4\ end {split} $$ |
| Paso 6. Cheque. | $$\ begin {split}\ dfrac {4} {3} &\ stackrel {?} {=}\ dfrac {\ textcolor {rojo} {6}} {4.5}\ qquad\ qquad\ qquad\ dfrac {4} {3}\ stackrel {?} {=}\ dfrac {3.2} {\ textcolor {rojo} {2.4}}\\ 4 (4.5) &\ stackrel {?} {=} 6 (3)\ qquad\ qquad\; 4 (2.4)\ stackrel {?} {=} 3.2 (3)\\ 18 &= 18\;\ marca de verificación\ qquad\ qquad\ quad\ cuádruple\; 9.6 = 9.6\;\ marca de verificación\ end {split} $$ |
| Paso 7. Contesta la pregunta. | El tercer lado de ΔABC es 6 y el tercer lado de ΔXYZ es 2.4. |
ΔABC es similar a ΔXYZ. Encuentra un.
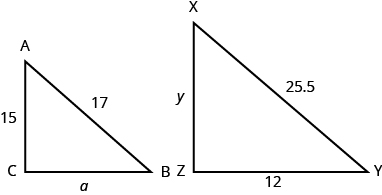
- Contestar
-
a = 8
ΔABC es similar a ΔXYZ. Encuentra y.

- Contestar
-
y = 22.5