9.S: Modelos Matemáticos y Geometría (Resumen)

Términos Clave

ángulo	Un ángulo está formado por dos rayos que comparten un punto final común. A cada rayo se le llama un lado del ángulo.
zona	El área es una medida de la superficie cubierta por una figura.
ángulos complementarios	Si la suma de las medidas de dos ángulos es de 90°, entonces se les llama ángulos complementarios.
cono	Un cono es una figura sólida con una base circular y un vértice.
cubo	Un cubo es un sólido rectangular cuya longitud, anchura y altura son iguales.
cilindro	Un cilindro es una figura sólida con dos círculos paralelos del mismo tamaño en la parte superior e inferior.
triángulo equilátero	Un triángulo con los tres lados de igual longitud se llama triángulo equilátero.
hipotenusa	El lado del triángulo opuesto al ángulo de 90° se llama hipotenusa.
figura irregular	Una figura que no es una forma geométrica estándar. Su área no se puede calcular utilizando ninguna de las fórmulas de área estándar.
triángulo isósceles	Un triángulo con dos lados de igual longitud se llama triángulo isósceles.
patas de un triángulo rectángulo	Los lados de un triángulo rectángulo adyacentes al ángulo recto
perímetro	El perímetro es una medida de la distancia alrededor de una figura.
rectángulo	Una figura geométrica que tiene cuatro lados y cuatro ángulos rectos.
triángulo rectángulo	Un triángulo que tiene un ángulo de 90°.
cifras similares	En geometría, si dos figuras tienen exactamente la misma forma pero diferentes tamaños, decimos que son figuras similares.
ángulos suplementarios	Si la suma de las medidas de dos ángulos es de 180°, entonces se denominan ángulos suplementarios.
trapecio	Una figura de cuatro lados, un cuadrilátero, con dos lados que son paralelos y dos lados que no lo son.
triángulo	Una figura geométrica con tres lados y tres ángulos.
vértice de un ángulo	Cuando dos rayos se encuentran para formar un ángulo, el punto final común se llama el vértice del ángulo.

Conceptos clave

9.1 - Usar una estrategia de resolución de problemas

• Estrategia de resolución de problemas
  1. Lee la palabra problema. Asegúrate de entender todas las palabras e ideas. Es posible que tengas que leer el problema dos o más veces. Si hay palabras que no entiendes, búscalas en un diccionario o en internet.
  2. Identifica lo que buscas.
  3. Nombra lo que buscas. Elija una variable para representar esa cantidad.
  4. Traducir en una ecuación. Puede ser útil volver a plantear primero el problema en una oración antes de traducirlo.
  5. Resolver la ecuación usando buenas técnicas de álgebra.
  6. Consulta la respuesta en el problema. Asegúrate de que tenga sentido.
  7. Contesta la pregunta con una oración completa.

9.2 - Resolver aplicaciones de dinero

• Encontrar el valor total de las monedas del mismo tipo
  • Para monedas del mismo tipo, el valor total se puede encontrar de la siguiente manera: $$número\ cdot valor = total\; valor$$donde número es el número de monedas, valor es el valor de cada moneda, y valor total es el valor total de todas las monedas.
• Resolver un problema de palabras de monedas
  1. Lee el problema. Asegúrate de entender todas las palabras e ideas, y crea una tabla para organizar la información.
  2. Identifica lo que buscas.
  3. Nombra lo que buscas. Elija una variable para representar esa cantidad.
     • Usa expresiones variables para representar el número de cada tipo de moneda y escríbelas en la tabla.
     • Multiplique el número por el valor para obtener el valor total de cada tipo de moneda.
  4. Traducir en una ecuación. Escribe la ecuación sumando los valores totales de todos los tipos de monedas.
  5. Resolver la ecuación usando buenas técnicas de álgebra.
  6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
  7. Contesta la pregunta con una oración completa.

Cuadro 9.16

Tipo	Número	Valor ($)	Valor Total ($)

9.3 - Propiedades de Uso de Ángulos, Triángulos y Teorema de Pitágoras

• Ángulos suplementarios y complementarios
  • Si la suma de las medidas de dos ángulos es 180°, entonces los ángulos son suplementarios.
  • Si A y B son suplementarios, entonces ma + mb = 180.
  • Si la suma de las medidas de dos ángulos es 90°, entonces los ángulos son complementarios.
  • Si A y B son complementarios, entonces ma + mb = 90.
• Resolver aplicaciones de geometría
  1. Lee el problema y asegúrate de entender todas las palabras e ideas. Dibuja una figura y etiquétela con la información dada.
  2. Identifica lo que buscas.
  3. Nombra lo que buscas y elige una variable para representarlo.
  4. Traducir en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
  5. Resolver la ecuación usando buenas técnicas de álgebra.
  6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
  7. Contesta la pregunta con una oración completa.
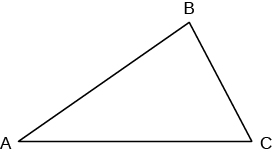
• Suma de las Medidas de los Ángulos de un Triángulo
  • Para cualquier ΔABC, la suma de las medidas es 180°
  • Ma + Mb = 180

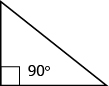
• Triángulo Recto
  • Un triángulo rectángulo es un triángulo que tiene un ángulo de 90°, que a menudo se marca con un símbolo.

• Propiedades de Triángulos Similares
  • Si dos triángulos son similares, entonces sus medidas de ángulo correspondientes son iguales y sus longitudes laterales correspondientes tienen la misma relación.

9.4 - Propiedades de Uso de Rectángulos, Triángulos y Trapecios

• Propiedades de Rectángulos
  • Los rectángulos tienen cuatro lados y cuatro ángulos rectos (90°).
  • Las longitudes de lados opuestos son iguales.
  • El perímetro, P, de un rectángulo es la suma del doble de la longitud y del doble de la anchura. $$P = 2L + 2W$$
  • El área, A, de un rectángulo es la longitud por la anchura. $$A = L\ cdot W$
• Propiedades de Triángulo
  • Para cualquier triángulo ΔABC, la suma de las medidas de los ángulos es 180°. $$m\ ángulo A + m\ ángulo B + m\ ángulo C = 180°$$
  • El perímetro de un triángulo es la suma de las longitudes de los lados. $$P = a + b + c$$
  • El área de un triángulo es la mitad de la base, b, multiplicada por la altura, H.$$a =\ dfrac {1} {2} bh$$

9.5 - Resolver aplicaciones de geometría: círculos y figuras irregulares

• Estrategia de resolución de problemas para aplicaciones de geometría
  1. Lee el problema y asegúrate de entender todas las palabras e ideas. Dibuja la figura y etiquétela con la información dada.
  2. Identifica lo que buscas.
  3. Nombra lo que buscas. Elija una variable para representar esa cantidad.
  4. Traducir en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
  5. Resolver la ecuación usando buenas técnicas de álgebra.
  6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
  7. Contesta la pregunta con una oración completa.
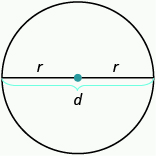
• Propiedades de Circles
  • d = 2r
  • Circunferencia: C = 2\(\pi\) r o C =\(\pi\) d
  • Área: A =\(\pi\) r ²

9.6 - Aplicaciones de Resolver Geometría: Volumen y Área de Superficie

• Volumen y Área de Superficie de un Sólido Rectangular
  • V = LWH
  • S = 2LH + 2LW + 2WH
• Volumen y superficie de un cubo
  • V = s ³
  • S = 6s ²
• Volumen y superficie de una esfera
  • V =\(\dfrac{4}{3} \pi\) r ³
  • S = 4\(\pi\) r ²
• Volumen y superficie de un cilindro
  • V =\(\pi\) r ² h
  • S = 2\(\pi\) r ² + 2\(\pi\) rh
• Volumen de un Cono
  • Para un cono con radio r y altura h: Volumen: V =\(\dfrac{1}{3} \pi\) r ² h

9.7 - Resolver una fórmula para una variable específica

• Distancia, velocidad y tiempo
  • d = rt

Colaboradores y Atribuciones

• Template:ContribOpenStaxPreAlgebra