9.11: Resolver una fórmula para una variable específica
- Page ID
- 114183
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usa la fórmula de distancia, velocidad y tiempo
- Resolver una fórmula para una variable específica
¡
Antes de comenzar, toma este cuestionario de preparación.
- Escribe 35 millas por galón como tarifa unitaria. Si te perdiste este problema, revisa el Ejemplo 5.11.8.
- Resuelve 6x + 24 = 96. Si te perdiste este problema, revisa el Ejemplo 8.4.1.
- Encuentra el interés simple ganado después de 5 años en $1,000 a una tasa de interés del 4%. Si te perdiste este problema, revisa el Ejemplo 6.4.1.
Utilice la fórmula de distancia, tasa y tiempo
Una fórmula que usarás a menudo en álgebra y en la vida cotidiana es la fórmula para la distancia recorrida por un objeto que se mueve a una velocidad constante. Probablemente ya te sea familiar la idea básica. ¿Sabes qué distancia recorres si conduces a un ritmo constante de 60 millas por hora durante 2 horas? (Esto podría suceder si usas el control de crucero de tu auto mientras conduces por la Interestatal). Si dijiste 120 millas, ¡ya sabes cómo usar esta fórmula!
La matemática para calcular la distancia podría verse así:
\[\begin{split} distance &= \left(\dfrac{60\; miles}{1\; hour}\right) (2\; hours) \\ distance &= 120\; miles \end{split}\]
En general, la fórmula que relaciona distancia, velocidad y tiempo es
\[distance = rate \cdot time\]
Para un objeto que se mueve a una velocidad uniforme (constante), la distancia recorrida, el tiempo transcurrido y la velocidad están relacionados por la fórmula
\[d = rt\]
donde d = distancia, r = tasa y t = tiempo.
Observe que las unidades que usamos anteriormente para la tarifa fueron millas por hora, las cuales podemos escribir como proporción\(\dfrac{miles}{hour}\). Entonces cuando multiplicamos por el tiempo, en horas, las unidades comunes 'hora' dividieron. La respuesta fue en millas.
Jamal monta su bicicleta a una tarifa uniforme de 12 millas por hora durante\(3 \dfrac{1}{2}\) horas. ¿Cuánta distancia ha recorrido?
Solución
| Paso 1. Lee el problema. Es posible que desee crear un mini-gráfico para resumir la información en el problema. | $$\ begin {split} d &=\;? \\ r &= 12\; mph\\ t &= 3\ dfrac {1} {2}\; horas\ end {split} $$ |
| Paso 2. Identifica lo que buscas. | distancia recorrida |
| Paso 3. Nombre. Elija una variable para representarla. | let d = distancia |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación. Sustituir en la información dada. | $$\ begin {split} d &= rt\\ d &= 12\ cdot 3\ dfrac {1} {2}\ end {split} $$ |
| Paso 5. Resuelve la ecuación. | d = 42 millas |
| Paso 6. Cheque: ¿Tiene sentido 42 millas? |  |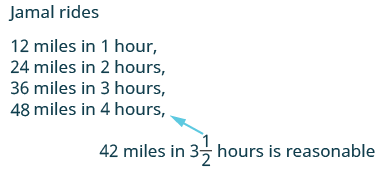
| Paso 7. Contesta la pregunta con una oración completa. | Jamal cabalgó 42 millas. |
Lindsay manejó durante\(5 \dfrac{1}{2}\) horas a 60 millas por hora. ¿Cuánta distancia recorrió?
- Contestar
-
330 mi
Trinh caminó durante\(2 \dfrac{1}{3}\) horas a 3 millas por hora. ¿Qué tan lejos caminó?
- Contestar
-
7 mi
Rey planea conducir desde su casa en San Diego para visitar a su abuela en Sacramento, a una distancia de 520 millas. Si puede conducir a un ritmo constante de 65 millas por hora, ¿cuántas horas tomará el viaje?
Solución
| Paso 1. Lee el problema. Resumir la información en el problema. | $$\ begin {split} d &= 520\; millas\\ r &= 65\; mph\\ t &=\;? \ end {split} $$ |
| Paso 2. Identifica lo que buscas. | cuántas horas (tiempo) |
| Paso 3. Nombre. Elija una variable para representarla. | let t = tiempo |
| Paso 4. Traducir. Escribir la fórmula apropiada para la situación. Sustituir en la información dada. | $$\ begin {split} d &= rt\\ 520 &= 65t\ end {split} $$ |
| Paso 5. Resuelve la ecuación. | t = 8 |
| Paso 6. Cheque: Sustituya los números en la fórmula y asegúrese de que el resultado sea una declaración verdadera. | $$\ begin {split} d &= rt\\ 520 &\ stackrel {?} {=} 65\ cdot 8\\ 520 &= 520\;\ marca de verificación\ final {dividir} $$ |
| Paso 7. Contesta la pregunta con una oración completa. Sabemos que las unidades de tiempo serán horas porque dividimos millas por millas por hora. | El viaje de Rey tomará 8 horas. |
Lee quiere conducir desde Phoenix hasta el departamento de su hermano en San Francisco, a una distancia de 770 millas. Si conduce a un ritmo constante de 70 millas por hora, ¿cuántas horas tomará el viaje?
- Contestar
-
11 horas
Yesenia está a 168 millas de Chicago. Si necesita estar en Chicago en 3 horas, ¿a qué ritmo necesita conducir?
- Contestar
-
56 mph
Resolver una fórmula para una variable específica
En este capítulo, te familiarizaste con algunas fórmulas utilizadas en geometría. Las fórmulas también son muy útiles en las ciencias y las ciencias sociales, campos como la química, la física, la biología, la psicología, la sociología y la justicia penal. Los trabajadores de la salud también usan fórmulas, incluso para algo tan rutinario como dispensar medicamentos. El programa de hojas de cálculo ampliamente utilizado Microsoft Excel TM se basa en fórmulas para hacer sus cálculos. Muchos profesores utilizan hojas de cálculo para aplicar fórmulas para calcular las calificaciones de los estudiantes. Es importante estar familiarizado con las fórmulas y poder manipularlas fácilmente.
En el Ejemplo 9.57 y en el Ejemplo 9.58, se utilizó la fórmula d = rt. Esta fórmula da el valor de d cuando se sustituye en los valores de r y t. Pero en el Ejemplo 9.58, tuvimos que encontrar el valor de t. Sustituimos en valores de d y r y luego usamos álgebra para resolver a t. Si tuvieras que hacer esto a menudo, tal vez te preguntes por qué no hay una fórmula que dé el valor de t cuando sustituto en los valores de d y r. podemos obtener una fórmula como esta resolviendo la fórmula d = rt para t.
Resolver una fórmula para una variable específica significa obtener esa variable por sí misma con un coeficiente de 1 en un lado de la ecuación y todas las demás variables y constantes en el otro lado. Llamaremos a esto resolver una ecuación para una variable específica en general. Este proceso también se llama resolver una ecuación literal. El resultado es otra fórmula, conformada únicamente por variables. La fórmula contiene letras, o literales.
Probemos algunos ejemplos, comenzando con la fórmula de distancia, tasa y tiempo que usamos anteriormente.
Resolver la fórmula d = rt para t: (a) cuando d = 520 y r = 65 (b) en general.
Solución
Escribiremos las soluciones lado a lado para que veas que resolver una fórmula en general usa los mismos pasos que cuando tenemos números para sustituir.
| (a) cuando d = 520 y r = 65 | b) en general | |
| Escribe la fórmula. | d = rt | d = rt |
| Sustituir cualquier valor dado. | 520 = 65t | |
| Dividir para aislar t. | $$\ dfrac {520} {65} =\ dfrac {65t} {65} $$ | $$\ dfrac {d} {r} =\ dfrac {rt} {r} $$ |
| Simplificar. | $$\ begin {split} 8 &= t\\ t &= 8\ end {split} $$ | $$\ begin {split}\ dfrac {d} {r} &= t\\ t &=\ dfrac {d} {r}\ end {split} $$ |
Observe que la solución para (a) es la misma que en el Ejemplo 9.58. Decimos que la fórmula t =\(\dfrac{d}{r}\) está resuelta para t. Podemos usar esta versión de la fórmula en cualquier momento que nos den la distancia y la tasa y necesitamos encontrar el tiempo.
Resolver la fórmula d = rt para r: (a) cuando d = 180 y t = 4 (b) en general
- Contestar a
-
\(r = 45\)
- Respuesta b
-
\(r = \frac{d}{t}\)
Resolver la fórmula d = rt para r: (a) cuando d = 780 y t = 12 (b) en general
- Contestar a
-
\(r = 65\)
- Respuesta b
-
\(r = \frac{d}{t}\)
Utilizamos la fórmula A =\(\dfrac{1}{2}\) bh en Propiedades de uso de rectángulos, triángulos y trapecios para encontrar el área de un triángulo cuando nos dieron la base y la altura. En el siguiente ejemplo, resolveremos esta fórmula para la altura.
La fórmula para el área de un triángulo es A =\(\dfrac{1}{2}\) bh. Resuelve esta fórmula para h: (a) cuando A = 90 y b = 15 (b) en general
Solución
| (a) cuando A = 90 y b = 15 | b) en general | |
| Escribe la fórmula. | A =\(\dfrac{1}{2}\) bh | A =\(\dfrac{1}{2}\) bh |
| Sustituir cualquier valor dado. | $$90 =\ dfrac {1} {2}\ cdot 15\ cdot h$$ | |
| Despeja las fracciones. | $$\ textcolor {rojo} {2}\ cdot 90 =\ textcolor {rojo} {2}\ cdot\ dfrac {1} {2}\ cdot 15\ cdot h$$ | $$\ textcolor {rojo} {2}\ cdot A =\ textcolor {rojo} {2}\ cdot\ dfrac {1} {2}\ cdot b\ cdot h$$ |
| Simplificar. | 180 = 15h | 2A = bh |
| Resolver por h. | 12 = h | \(\dfrac{2A}{b}\)= h |
Ahora podemos encontrar la altura de un triángulo, si conocemos el área y la base, usando la fórmula
\[h = \dfrac{2A}{b}\]
Usa la fórmula A =\(\dfrac{1}{2}\) bh para resolver para h: (a) cuando A = 170 y b = 17 (b) en general
- Contestar a
-
\(h = 20\)
- Respuesta b
-
\(h = \frac{2A}{b}\)
Usa la fórmula A =\(\dfrac{1}{2}\) bh para resolver para b: (a) cuando A = 62 y h = 31 (b) en general
- Contestar a
-
\(b = 4\)
- Respuesta b
-
\(b = \frac{2A}{h}\)
En Resolver aplicaciones de interés simple, utilizamos la fórmula I = Prt para calcular interés simple, donde I es interés, P es principal, r es tasa como decimal y t es tiempo en años.
Resuelve la fórmula I = Prt para encontrar el principal, P: (a) cuando I = $5,600, r = 4%, t = 7 años (b) en general
Solución
| (a) cuando I = $5,600, r = 4%, t = 7 años | b) en general | |
| Escribe la forumla. | I = Prt | I = Prt |
| Sustituir cualquier valor dado. | 5600 = P (0.04) (7) | I = Prt |
| Multiplicar r • t. | 5600 = P (0.28) | I = P (rt) |
| Dividir para aislar a P. | $$\ dfrac {5600} {\ textcolor {rojo} {0.28}} =\ dfrac {P (0.28)} {\ textcolor {rojo} {0.28}} $$ | $$\ dfrac {I} {\ textcolor {rojo} {rt}} =\ dfrac {P (rt)} {\ textcolor {rojo} {rt}} $$ |
| Simplificar. | 20,000 = P | \(\dfrac{I}{rt}\)= P |
| Exponga la respuesta. | El principal es de 20,000 dólares. | $$P =\ dfrac {I} {rt} $$ |
Usa la fórmula I = Prt. Encuentra t: (a) cuando I = $2,160, r = 6%, P = $12,000; (b) en general
- Contestar a
-
\(t = 3\)años
- Respuesta b
-
\(t = \frac{I}{Pr}\)
Usa la fórmula I = Prt. Encuentra r: (a) cuando I = $5,400, P = $9,000, t = 5 años; (b) en general
- Contestar a
-
\(r = 0.12 = 12\%\)
- Respuesta b
-
\(t = \frac{I}{Pt}\)
Más adelante en este curso, y en futuras clases de álgebra, encontrarás ecuaciones que relacionan dos variables, generalmente x e y, es posible que se te dé una ecuación que se solucione para y y necesite resolverla para x, o viceversa. En el siguiente ejemplo, se nos da una ecuación con tanto x como y en el mismo lado y la resolveremos para y Para ello, seguiremos los mismos pasos que usamos para resolver una fórmula para una variable específica.
Resuelve la fórmula 3x + 2y = 18 para y: (a) cuando x = 4 (b) en general
Solución
| (a) cuando x = 4 | b) en general | |
| Escribe la ecuación. | 3x + 2 años = 18 | 3x + 2 años = 18 |
| Sustituir cualquier valor dado. | 3 (4) + 2 años = 18 | 3x + 2 años = 18 |
| Simplificar si es posible. | 12 + 2 años = 18 | 3x + 2 años = 18 |
| Restar para aislar el término y. | $$12\ textcolor {rojo} {-12} + 2y = 18\ textcolor {rojo} {-12} $$ | $$3x\ textcolor {rojo} {-3x} + 2y = 18\ textcolor {rojo} {-3x} $$ |
| Simplificar. | 2 años = 6 | 2 años = 18 - 3x |
| Dividir. | $$\ dfrac {2y} {\ textcolor {rojo} {2}} =\ dfrac {6} {\ textcolor {rojo} {2}} $$ | $$\ dfrac {2y} {\ textcolor {rojo} {2}} =\ dfrac {18 - 3x} {\ textcolor {rojo} {2}} $$ |
| Simplificar. | y = 3 | $$y =\ dfrac {18 - 3x} {2} $$ |
Resuelve la fórmula 3x + 4y = 10 para y: (a) cuando x = 2 (b) en general
- Contestar a
-
\(y = 1\)
- Respuesta b
-
\(y = \frac{10-3x}{4}\)
Resuelve la fórmula 5x + 2y = 18 para y: (a) cuando x = 4 (b) en general
- Contestar a
-
\(y = -1\)
- Respuesta b
-
\(y = \frac{18-5x}{2}\)
En los ejemplos anteriores, utilizamos los números de la parte (a) como guía para resolver en general en la parte (b). ¿Crees que estás listo para resolver una fórmula en general sin usar números como guía?
Resuelve la fórmula P = a + b + c para a.
Solución
Aislaremos a en un lado de la ecuación.
| Aislaremos a en un lado de la ecuación. | |
| Escribe la ecuación. | P = a + b + c |
| Restar b y c de ambos lados para aislar a. | $$P\ textcolor {rojo} {-b -c} = a + b + c\ textcolor {rojo} {-b -c} $$ |
| Simplificar. | P − b − c = a |
Entonces, a = P − b − c.
Resuelve la fórmula P = a + b + c para b.
- Contestar
-
b = P - a - c
Resuelve la fórmula P = a + b + c para c.
- Contestar
- c = P - a - b
Resuelve la ecuación 3x + y = 10 para y.
Solución
Aislaremos y en un lado de la ecuación.
| Aislaremos y en un lado de la ecuación. | |
| Escribe la ecuación. | 3x + y = 10 |
| Restar 3x de ambos lados para aislar y. | $$3x\ textcolor {rojo} {-3x} + y= 10\ textcolor {rojo} {-3x} $$ |
| Simplificar. | y = 10 - 3x |
Resuelve la fórmula 7x + y = 11 para y
- Contestar
-
y = 11 - 7x
Resuelve la fórmula 11x + y = 8 para y.
- Contestar
-
y = 8 - 11x
Resuelve la ecuación 6x + 5y = 13 para y.
Solución
Aislaremos y en un lado de la ecuación.
| Aislaremos y en un lado de la ecuación. | |
| Escribe la ecuación. | 6x + 5y = 13 |
| Restar para aislar el término con y. | $$6x + 5y\ textcolor {rojo} {-6x} = 13\ textcolor {rojo} {-6x} $$ |
| Simplificar. | 5 años = 13 - 6x |
| Divida 5 para hacer el coeficiente 1. | $$\ dfrac {5y} {\ textcolor {rojo} {5}} =\ dfrac {13 - 6x} {\ textcolor {rojo} {5}} $$ |
| Simplificar. | $$y =\ dfrac {13 - 6x} {5} $$ |
Resuelve la fórmula 4x + 7y = 9 para y.
- Contestar
-
\(y = \frac{9-4x}{7}\)
Resuelve la fórmula 5x + 8y = 1 para y.
- Contestar
-
\(y = \frac{1-5x}{8}\)
La práctica hace la perfección
Utilice la fórmula de distancia, tasa y tiempo
En los siguientes ejercicios, resuelve.
- Steve manejó durante\(8 \dfrac{1}{2}\) horas a 72 millas por hora. ¿Cuánta distancia recorrió?
- Socorro manejó durante\(4 \dfrac{5}{6}\) horas a 60 millas por hora. ¿Cuánta distancia recorrió?
- Yuki caminó durante\(1 \dfrac{3}{4}\) horas a 4 millas por hora. ¿Qué tan lejos caminó?
- Francie montó su bicicleta durante\(2 \dfrac{1}{2}\) horas a 12 millas por hora. ¿Qué tan lejos cabalgó?
- Connor quiere conducir desde Tucson hasta el Gran Cañón, a una distancia de 338 millas. Si conduce a un ritmo constante de 52 millas por hora, ¿cuántas horas tomará el viaje?
- Megan toma el autobús de la ciudad de Nueva York a Montreal. La distancia es de 384 millas y el autobús viaja a un ritmo constante de 64 millas por hora. ¿Cuánto durará el viaje en autobús?
- Aurelia está conduciendo de Miami a Orlando a una tasa de 65 millas por hora. La distancia es de 235 millas. A la décima de hora más cercana, ¿cuánto durará el viaje?
- Kareem quiere andar en bicicleta desde St. Louis, Missouri hasta Champaign, Illinois. La distancia es de 180 millas. Si viaja a un ritmo constante de 16 millas por hora, ¿cuántas horas tomará el viaje?
- Javier está conduciendo a Bangor, Maine, que está a 240 millas de su ubicación actual. Si necesita estar en Bangor en 4 horas, ¿a qué ritmo necesita conducir?
- Alejandra está conduciendo a Cincinnati, Ohio, a 450 millas de distancia. Si quiere estar ahí en 6 horas, ¿a qué precio necesita conducir?
- Aisha tomó el tren de Spokane a Seattle. La distancia es de 280 millas, y el viaje duró 3.5 horas. ¿Cuál era la velocidad del tren?
- Philip consiguió un viaje con un amigo de Denver a Las Vegas, a una distancia de 750 millas. Si el viaje duró 10 horas, ¿qué tan rápido conducía el amigo?
Resolver una fórmula para una variable específica
En los siguientes ejercicios, use la fórmula. d = rt.
- Resolver para t: (a) cuando d = 350 y r = 70 (b) en general
- Resolver para t: (a) cuando d = 240 y r = 60 (b) en general
- Resolver para t: (a) cuando d = 510 y r = 60 (b) en general
- Resolver para t: (a) cuando d = 175 y r = 50 (b) en general
- Resolver para r: (a) cuando d = 204 y t = 3 (b) en general
- Resolver para r: (a) cuando d = 420 y t = 6 (b) en general
- Resolver para r: (a) cuando d = 160 y t = 2.5 (b) en general
- Resuelve para r: (a) cuando d = 180 y t = 4.5 (b) en general.
En los siguientes ejercicios, usa la fórmula A =\(\dfrac{1}{2}\) bh.
- Resolver para b: (a) cuando A = 126 y h = 18 (b) en general
- Resolver para h: (a) cuando A = 176 y b = 22 (b) en general
- Resolver para h: (a) cuando A = 375 y b = 25 (b) en general
- Resolver para b: (a) cuando A = 65 y h = 13 (b) en general
En los siguientes ejercicios, usa la fórmula I = Prt.
- Resuelve para el principal, P para: (a) I = $5,480, r = 4%, t = 7 años (b) en general
- Resuelve para el principal, P para: (a) I = $3,950, r = 6%, t = 5 años (b) en general
- Resuelve por el tiempo, t para: (a) I = $2,376, P = $9,000, r = 4.4% (b) en general
- Resuelve por el tiempo, t para: (a) I = 624 dólares, P = $6,000, r = 5.2% (b) en general
En los siguientes ejercicios, resuelve.
- Resuelve la fórmula 2x + 3y = 12 para y: (a) cuando x = 3 (b) en general
- Resuelve la fórmula 5x + 2y = 10 para y: (a) cuando x = 4 (b) en general
- Resuelve la fórmula 3x + y = 7 para y: (a) cuando x = −2 (b) en general
- Resuelve la fórmula 4x + y = 5 para y: (a) cuando x = −3 (b) en general
- Resuelve a + b = 90 para b.
- Resuelve a + b = 90 para a.
- Resuelve 180 = a + b + c para a.
- Resuelve 180 = a + b + c para c.
- Resuelve la fórmula 8x + y = 15 para y.
- Resuelve la fórmula 9x + y = 13 para y.
- Resuelve la fórmula −4x + y = −6 para y.
- Resuelve la fórmula −5x + y = −1 para y.
- Resuelve la fórmula 4x + 3y = 7 para y.
- Resuelve la fórmula 3x + 2y = 11 para y.
- Resuelve la fórmula x − y = −4 para y.
- Resuelve la fórmula x − y = −3 para y.
- Resuelve la fórmula P = 2L + 2W para L.
- Resuelve la fórmula P = 2L + 2W para W.
- Resuelve la fórmula C =\(\pi\) d para d.
- Resuelve la fórmula C =\(\pi\) d para\(\pi\).
- Resuelve la fórmula V = LWH para L.
- Resuelve la fórmula V = LWH para H.
Matemáticas cotidianas
- Conversión de temperatura Mientras estaba de gira por Grecia, Tatyana vio que la temperatura era de 40° Celsius. Resuelve F en la fórmula C =\(\dfrac{5}{9}\) (F − 32) para encontrar la temperatura en Fahrenheit.
- Convirtiendo temperatura Yon estaba de visita por Estados Unidos y vio que la temperatura en Seattle era de 50° Fahrenheit. Resuelve para C en la fórmula F =\(\dfrac{9}{5}\) C + 32 para encontrar la temperatura en Celsius.
Ejercicios de escritura
- Resuelve la ecuación 2x + 3y = 6 para y: (a) cuando x = −3 (b) en general (c) ¿Cuál solución es más fácil para ti? Explique por qué.
- Resuelve la ecuación 5x − 2y = 10 para x: (a) cuando y = 10 (b) en general (c) ¿Cuál solución es más fácil para ti? Explique por qué.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
(b) En general, después de mirar la lista de verificación, ¿cree que está bien preparado para el próximo Capítulo? ¿Por qué o por qué no?