Saltar al contenido principal
LibreTexts Español

1.4.1: Ángulos interiores alternos

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118674

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lección

    Exploremos por qué algunos ángulos son siempre iguales.

    Ejercicio\(\PageIndex{1}\): Angle Pairs

    1. Encuentra la medida del ángulo\(JGH\). Explica o muestra tu razonamiento.

    clipboard_e23f8033101115e1b86614db2895e64cb.png
    Figura\(\PageIndex{1}\)

    2. Encuentre y etiquete un ángulo\(30^{\circ}\) de segundo grado en el diagrama. Encuentre y etiquete un ángulo congruente con el ángulo\(JGH\).

    Ejercicio\(\PageIndex{2}\): Cutting Parallel Lines with a Transversal

    Líneas\(AC\) y\(DF\) son paralelas. Se cortan por transversal\(HJ\).

    clipboard_ea6ad235b3f4961f8590478ead6f28542.png
    Figura\(\PageIndex{2}\): La línea A C contiene el punto B. La línea D F contiene el punto E. La línea J H contiene los puntos B y E. El ángulo A B J está etiquetado como signo de interrogación. El ángulo A B E está etiquetado 63 grados. El ángulo E B C está etiquetado como signo de interrogación. El ángulo C B J está etiquetado como signo de interrogación. El ángulo D E H está etiquetado como signo de interrogación. El ángulo H E F está etiquetado como signo de interrogación. El ángulo F E B está etiquetado como signo de interrogación. El ángulo B E D está etiquetado como signo de interrogación.
    1. Con tu pareja, encuentra las siete medidas de ángulo desconocidas en el diagrama. Explica tu razonamiento.
    2. ¿Qué notas sobre los ángulos con vértice\(B\) y los ángulos con vértice\(E\)?
    3. Usando lo que notaste, encuentra las medidas de los cuatro ángulos en punto\(B\) en el segundo diagrama. Líneas\(AC\) y\(DF\) son paralelas.
    clipboard_e8faa34d53e0a6204a7c52fcc3be68420.png
    Figura\(\PageIndex{3}\): La línea A C contiene el punto B. La línea D F contiene el punto E. La línea H G contiene los puntos B y E. El ángulo A B H está etiquetado con un signo de interrogación. El ángulo A B E está etiquetado con un signo de interrogación. El ángulo E B C está etiquetado con un signo de interrogación. El ángulo C B H está etiquetado con un signo de interrogación. El ángulo G E F está etiquetado como 34 grados.

    4. El siguiente diagrama se asemeja al primero, pero las líneas forman ángulos ligeramente diferentes. Trabaja con tu pareja para encontrar los seis ángulos desconocidos con vértices en puntos\(B\) y\(E\).

    clipboard_e81e6d57953a8eeee4951a25e50e32fa3.png
    Figura\(\PageIndex{4}\): La línea A C contiene el punto B. La línea D F contiene el punto E. La línea J H contiene los puntos B y E. El ángulo A B J está etiquetado como signo de interrogación. El ángulo A B E está etiquetado 63 grados. El ángulo E B C está etiquetado como signo de interrogación. El ángulo C B J está etiquetado como signo de interrogación. El ángulo D E H está etiquetado como signo de interrogación. El ángulo H E F está etiquetado como 108 grados. El ángulo F E B está etiquetado como signo de interrogación. El ángulo B E D está etiquetado como signo de interrogación.

    5. ¿Qué nota acerca de los ángulos en este diagrama en comparación con el diagrama anterior? ¿En qué se diferencian los dos diagramas? ¿Cómo son iguales?

    ¿Estás listo para más?

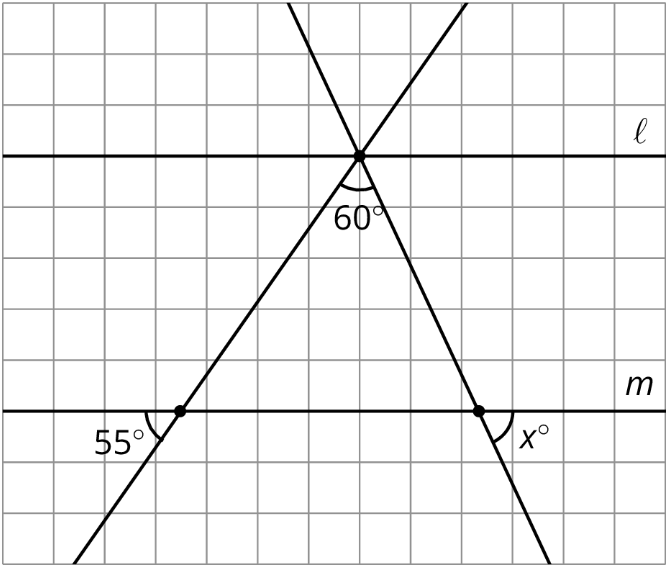
    clipboard_ec9b8d69013ac624d26b77bcbd799449f.png
    Figura\(\PageIndex{5}\): Cuatro líneas en una cuadrícula. La línea l es una línea horizontal 8 unidades arriba en la rejilla. La línea m es una línea horizontal 3 unidades arriba en la rejilla. Una línea avanza hacia arriba y hacia la derecha y cruza la línea m en un punto entre 3 y 4 unidades a la derecha y 3 unidades hacia arriba. La línea cruza la línea l en un punto 7 unidades a la derecha y 8 unidades hacia arriba. Otra línea cruza la línea m en un punto entre 9 y 10 unidades a la derecha y 3 unidades hacia arriba. Cruza la línea l en un punto 7 unidades a la derecha y 8 unidades hacia arriba. El ángulo interior en la parte superior del triángulo formado está etiquetado 60 grados. El ángulo exterior inferior izquierdo del vértice inferior izquierdo está etiquetado 55 grados. El ángulo exterior derecho inferior del vértice inferior derecho está etiquetado x grados.

    Las líneas paralelas\(l\) y\(m\) están cortadas por dos transversales que se cruzan\(l\) en un mismo punto. Dos ángulos están marcados en la figura. Encuentra la medida\(x\) del tercer ángulo.

    Ejercicio\(\PageIndex{3}\): Alternate Interior Angles are Congruent

    1. Líneas\(l\) y\(k\) son paralelas y\(t\) es una transversal. El punto\(M\) es el punto medio del segmento\(PQ\).

    clipboard_e45fd24f4f386b0b20b1033b417745a84.png
    Figura\(\PageIndex{6}\)

    Encuentra una transformación rígida que muestre que los ángulos\(MPA\) y\(MQB\) son congruentes.

    2. En esta imagen, las líneas\(l\) y ya no\(k\) son paralelas. \(M\)sigue siendo el punto medio del segmento\(PQ\).

    clipboard_eda95d16c2ab15a03194f9bb2af89e7e9.png
    Figura\(\PageIndex{7}\)

    ¿Su argumento en el problema anterior se aplica en esta situación? Explique.

    Resumen

    Cuando dos líneas se cruzan, los ángulos verticales son iguales y los ángulos adyacentes son complementarios, es decir, sus medidas suman 180\(^{\circ}\). Por ejemplo, en esta figura los ángulos 1 y 3 son iguales, los ángulos 2 y 4 son iguales, los ángulos 1 y 4 son complementarios y los ángulos 2 y 3 son suplementarios.

    clipboard_ea66acde88131eadedcad1f4b02f90514.png
    Figura\(\PageIndex{8}\): Dos líneas de intersección. El ángulo 1 está etiquetado como 70 grados. El ángulo 2 está etiquetado como 110 grados. El ángulo 3 está etiquetado como 70 grados. El ángulo 4 está etiquetado como 110 grados.

    Cuando dos líneas paralelas son cortadas por otra línea, llamada transversal, se crean dos pares de ángulos interiores alternos. (“Interior” significa en el interior, o entre, las dos líneas paralelas.) Por ejemplo, en esta figura los ángulos 3 y 5 son ángulos interiores alternos y los ángulos 4 y 6 también son ángulos interiores alternos.

    clipboard_e32331a9061edf85f05fca8eb4a4a17e5.png
    Figura\(\PageIndex{9}\): Dos líneas que no se cruzan. Una tercera línea se cruza con ambas líneas. En la primera intersección, el ángulo 1 está etiquetado como 70 grados. El ángulo 2 está etiquetado como 110 grados. El ángulo 3 está etiquetado como 70 grados. El ángulo 4 está etiquetado como 110 grados. En la segunda intersección, el ángulo 5 está marcado 70 grados. El ángulo 6 está marcado 110 grados. El ángulo 7 está marcado 70 grados. El ángulo 8 está marcado 110 grados.

    Los ángulos interiores alternos son iguales porque una\(180^{\circ}\) rotación alrededor del punto medio del segmento que une sus vértices lleva cada ángulo al otro. Imagínese un punto\(M\) a medio camino entre las dos intersecciones: ¿puede ver\(180^{\circ}\) cómo girar\(M\) toma el ángulo 3 al ángulo 5?

    Usando lo que sabemos sobre ángulos verticales, ángulos adyacentes y ángulos interiores alternos, podemos encontrar las medidas de cualquiera de los ocho ángulos creados por una transversal si conocemos solo uno de ellos. Por ejemplo, comenzando por el hecho de que el ángulo 1 es\(70^{\circ}\) usamos ángulos verticales para ver que el ángulo 3 es\(70^{\circ}\), luego usamos ángulos interiores alternos para ver que el ángulo 5 es\(70^{\circ}\), entonces usamos el hecho de que el ángulo 5 es complementario al ángulo 8 para ver que el ángulo 8 es\(110^{\circ}\) desde\(180-70=110\). Resulta que sólo hay dos medidas diferentes. En este ejemplo, los ángulos 1, 3, 5 y 7 miden\(70^{\circ}\), y los ángulos 2, 4, 6 y 8 miden\(110^{\circ}\).

    Entradas en el glosario

    Definición: Ángulos interiores alternos

    Los ángulos interiores alternos se crean cuando dos líneas paralelas son cruzadas por otra línea llamada transversal. Los ángulos interiores alternos están dentro de las líneas paralelas y en lados opuestos de la transversal.

    Este diagrama muestra dos pares de ángulos interiores alternos. Los ángulos\(a\) y\(d\) son un par y los ángulos\(b\) y\(c\) son otro par.

    clipboard_e4756004d866f53bde0723ab9232e8d0c.png
    Figura\(\PageIndex{10}\): Hay dos líneas paralelas horizontales, y una tercera línea diagonal dibujada desde la parte inferior izquierda hasta la parte superior derecha, intersectando ambas líneas horizontales. La línea diagonal se etiqueta transversal. Hay cuatro ángulos creados por la línea diagonal dentro de las líneas paralelas. El ángulo superior izquierdo está etiquetado como a, superior derecha es b, inferior izquierda es c e inferior derecha es d.

    Definición: Transversal

    Una transversal es una línea que cruza líneas paralelas.

    Este diagrama muestra una línea transversal\(k\) que cruza líneas paralelas\(m\) y\(l\).

    clipboard_ed76014d822bc3ca0adff616e885471aa.png
    Figura\(\PageIndex{11}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    Usa el daigrama para encontrar la medida de cada ángulo.

    1. \(m\angle ABC\)
    2. \(m\angle EBD\)
    3. \(m\angle ABE\)
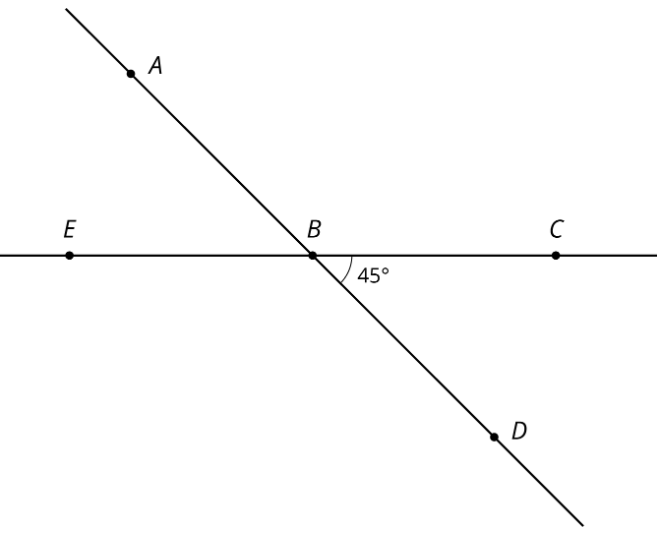
    clipboard_ef2844e61d28feb2b47588b3d9faa4221.png
    Figura\(\PageIndex{12}\): Una línea horizontal y una línea que se incline hacia abajo de izquierda a derecha. Las líneas se cruzan en un punto etiquetado como B. En la línea horizontal, el punto E está a la izquierda de B y C está a la derecha de B. En la línea inclinada, el punto A está por encima de B y el punto D está por debajo de B. El ángulo C B D está etiquetado 45 grados.

    (De la Unidad 1.2.3)

    Ejercicio\(\PageIndex{5}\)

    Líneas\(k\) y\(l\) son paralelas, y la medida del ángulo\(ABC\) es de 19 grados.

    clipboard_e9eb683708436e4febe010408e6e4068c.png
    Figura\(\PageIndex{13}\): Dos líneas paralelas, k y l, cortadas por la línea transversal m. Los puntos F, C y D están en la línea k. Los puntos A y B están en la línea l. Los puntos E, C y B están en m transversal. El ángulo E C F se marca congruente con el ángulo D C B y con el ángulo A B C.
    1. Explique por qué la medida del ángulo\(ECF\) es de 19 grados. Si te quedas atascado, considera traducir la línea moviéndote\(B\) a\(C\).
    2. ¿Cuál es la medida del ángulo\(BCD\)? Explique.

    Ejercicio\(\PageIndex{6}\)

    El diagrama muestra tres líneas con algunas medidas de ángulo marcadas.

    clipboard_e1a65ebe823a538858572527141f32449.png
    Figura\(\PageIndex{14}\): Dos líneas que no se cruzan. Una tercera línea se cruza con ambas líneas. En la primera intersección, los ángulos se marcan comenzando en la parte superior derecha y yendo en sentido horario, 70 grados, signo de interrogación, signo de interrogación, signo de interrogación. En la segunda intersección, los ángulos se marcan comenzando en la parte superior derecha y yendo en sentido horario, 53 grados, signo de interrogación, signo de interrogación, signo de interrogación.

    Encuentra las medidas de ángulo faltantes marcadas con signos de interrogación.

    Ejercicio\(\PageIndex{7}\)

    Líneas\(s\) y\(t\) son paralelas. Encuentra el valor de\(x\).

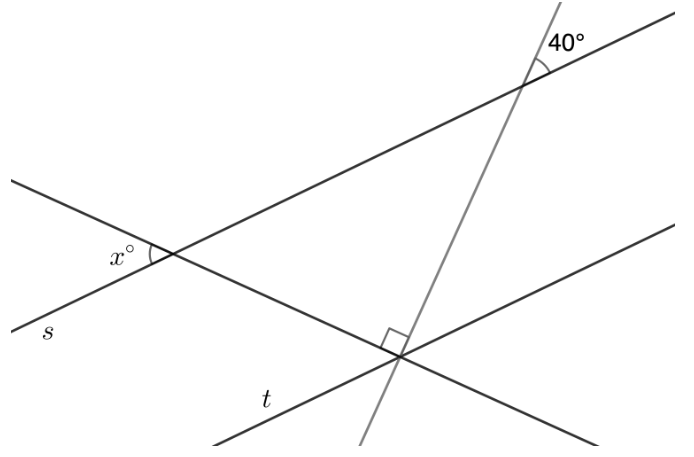
    clipboard_e960e9328d0178a52ef65de3789925c89.png
    Figura\(\PageIndex{15}\)

    Ejercicio\(\PageIndex{8}\)

    Las dos figuras son copias escaladas entre sí.

    1. ¿Cuál es el factor de escala que lleva de la Figura 1 a la Figura 2?
    2. ¿Cuál es el factor de escala que lleva la Figura 2 a la Figura 1?
    clipboard_eb49f9233f1fd8d1b03216c0d2d74df09.png
    Figura 2.

    This page titled 1.4.1: Ángulos interiores alternos is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.