1.4.2: Sumando los ángulos en un triángulo

Lección

Exploremos ángulos en triángulos.

Ejercicio\(\PageIndex{1}\): Can You Draw It?

1. Complete la tabla dibujando un triángulo en cada celda que tenga las propiedades listadas para su columna y fila. Si crees que no puedes dibujar un triángulo con esas propiedades, escribe “imposible” en la celda.
2. Comparte tus dibujos con un compañero. Discuta tu pensamiento. Si no estás de acuerdo, trabaja para llegar a un acuerdo.

Mesa\(\PageIndex{1}\)

	agudo (todos los ángulos agudos)	derecha (tiene un ángulo recto)	obtuso (tiene un ángulo obtuso)
escaleno (longitudes laterales todas diferentes)
isósceles (al menos dos longitudes laterales son iguales)
equilátero (tres longitudes laterales iguales)

Ejercicio\(\PageIndex{2}\): Find All Three

Tu profesor te entregará una tarjeta con una imagen de un triángulo.

1. La medición de uno de los ángulos está etiquetada. Estimar mentalmente las medidas de los otros dos ángulos.
2. Encuentra a otros dos alumnos con triángulos congruentes a los tuyos pero con un ángulo distinto etiquetado. Confirma que los triángulos son congruentes, que cada carta tiene un ángulo diferente etiquetado, y que las medidas del ángulo tienen sentido.
3. Ingresa las tres medidas de ángulo para tu triángulo en la mesa que tu profesor haya publicado.

Ejercicio\(\PageIndex{3}\): Tear It Up

Tu profesor te dará una página con tres juegos de ángulos y un espacio en blanco. Recorta cada juego de tres ángulos. ¿Se puede hacer un triángulo de cada conjunto que tenga estos mismos tres ángulos?

¿Estás listo para más?

1. Dibuja un cuadrilátero. Cortarlo, arrancar sus ángulos, y alinearlos. ¿Qué notas?
2. Repita esto para varios cuadriláteros más. ¿Tienes alguna conjetura sobre los ángulos?

Resumen

A un\(180^{\circ}\) ángulo se le llama ángulo recto porque cuando se hace con dos rayos, apuntan en direcciones opuestas y forman una línea recta.

Figura\(\PageIndex{1}\)

Si experimentamos con ángulos en un triángulo, encontramos que la suma de las medidas de los tres ángulos en cada triángulo es\(180^{\circ}\) —lo mismo que un ángulo recto!

A través de la experimentación encontramos:

• Si agregamos los tres ángulos de un triángulo físicamente cortándolos y alineando los vértices y lados, entonces los tres ángulos forman un ángulo recto.
• Si tenemos una línea y dos rayos que forman tres ángulos añadidos para hacer un ángulo recto, entonces hay un triángulo con estos tres ángulos.

Figura\(\PageIndex{2}\)

Entradas en el glosario

Definición: Ángulos interiores alternos

Los ángulos interiores alternos se crean cuando dos líneas paralelas son cruzadas por otra línea llamada transversal. Los ángulos interiores alternos están dentro de las líneas paralelas y en lados opuestos de la transversal.

Este diagrama muestra dos pares de ángulos interiores alternos. Los ángulos\(a\) y\(d\) son un par y los ángulos\(b\) y\(c\) son otro par.

Figura\(\PageIndex{3}\): Hay dos líneas paralelas horizontales, y una tercera línea diagonal dibujada desde la parte inferior izquierda hasta la parte superior derecha, intersectando ambas líneas horizontales. La línea diagonal está etiquetada como transversal. Hay cuatro ángulos creados por la línea diagonal dentro de las líneas paralelas. El ángulo superior izquierdo está etiquetado como a, superior derecha es b, inferior izquierda es c e inferior derecha es d.

Definición: Ángulo recto

Un ángulo recto es un ángulo que forma una línea recta. Mide 180 grados.

Figura\(\PageIndex{4}\)

Definición: Transversal

Una transversal es una línea que cruza líneas paralelas.

Este diagrama muestra una línea transversal\(k\) que cruza líneas paralelas\(m\) y\(l\).

Figura\(\PageIndex{5}\)

Practica

Ejercicio\(\PageIndex{4}\)

En triángulo\(ABC\), la medida del ángulo\(A\) es\(40^{\circ}\).

1. Dar posibles medidas para ángulos\(B\) y\(C\) si triángulo\(ABC\) es isósceles.
2. Dar posibles medidas para los ángulos\(B\) y\(C\) si el triángulo\(ABC\) es recto.

Ejercicio\(\PageIndex{5}\)

Para cada conjunto de ángulos, decide si hay un triángulo cuyos ángulos tienen estas medidas en grados:

1. 60, 60
2. 90, 45
3. 30, 40, 50
4. 90, 45
5. 120, 30, 30

Si te atascas, considera hacer un segmento de línea. Luego usa un traslador para medir ángulos con las dos primeras medidas de ángulo.

Ejercicio\(\PageIndex{6}\)

El ángulo\(A\) en triángulo\(ABC\) es obtuso. ¿Puede el ángulo\(B\) o\(C\) el ángulo ser obtuso? Explica tu razonamiento.

Ejercicio\(\PageIndex{7}\)

Para cada par de polígonos, describa la transformación que podría aplicarse al Polígono A para obtener el Polígono B.

1.

Figura\(\PageIndex{6}\)

2.

Figura\(\PageIndex{7}\)

3.

Figura\(\PageIndex{8}\)

(De la Unidad 1.1.3)

Ejercicio\(\PageIndex{8}\)

En la cuadrícula, dibuje una copia a escala de cuadrilátero\(ABCD\) usando un factor de escala de\(\frac{1}{2}\).

Figura\(\PageIndex{9}\): Un cuadrilátero sobre una rejilla. El punto A es de 2 unidades a la derecha y 6 unidades arriba. El punto B es de 4 unidades a la derecha y 8 unidades arriba. El punto C es de 8 unidades a la derecha y 6 unidades arriba. El punto D es de 4 unidades a la derecha y 2 unidades arriba.

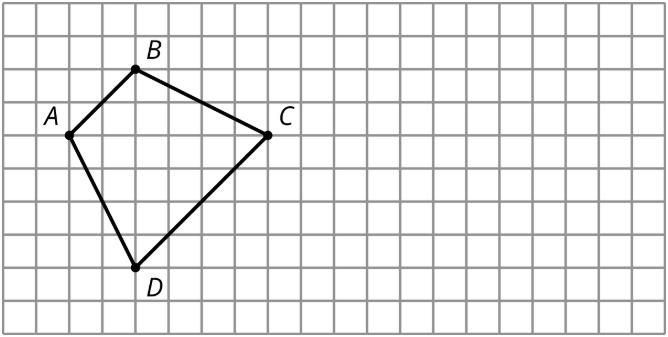
(De la Unidad 1.4.1)