Saltar al contenido principal
LibreTexts Español

1.4.3: Líneas paralelas y los ángulos en un triángulo

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118675

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    Lección

    Veamos por qué los ángulos en un triángulo suman 180 grados.

    Ejercicio\(\PageIndex{1}\): True or False: Computational Relationships

    ¿Cada ecuación es verdadera o falsa?

    \(62-28=60-30\)

    \(3\cdot -8=(2\cdot -8)-8\)

    \(\frac{16}{-2}+\frac{24}{-2}=\frac{40}{-2}\)

    Ejercicio\(\PageIndex{2}\): Angle Plus Two

    Considera triángulo\(ABC\). Seleccione la herramienta Punto medio y haga clic en dos puntos o un segmento para encontrar el punto medio.

    clipboard_e9f70bd471fe7bc624337abaaf5a7e039.png

    1. Gire el triángulo\(ABC\)\(180^{\circ}\) alrededor del punto medio del lado\(AC\). Haga clic derecho en el punto y seleccione Cambiar nombre para etiquetar el nuevo vértice\(D\).
    2. Gire el triángulo\(ABC\)\(180^{\circ}\) alrededor del punto medio del lado\(AB\). Haga clic derecho en el punto y seleccione Cambiar nombre para etiquetar el nuevo vértice\(E\).
    3. Mira los ángulos\(EAB\),\(BAC\), y\(CAD\). Sin medir, escribe lo que piensas que es la suma de las medidas de estos ángulos. Explica o muestra tu razonamiento.
    4. ¿La medida del ángulo es\(EAB\) igual a la medida de cualquier ángulo en triángulo\(ABC\)? Si es así, ¿cuál? Si no, ¿cómo lo sabes?
    5. ¿La medida del ángulo es\(CAD\) igual a la medida de cualquier ángulo en triángulo\(ABC\)? Si es así, ¿cuál? Si no, ¿cómo lo sabes?
    6. ¿Cuál es la suma de las medidas de los ángulos\(ABC\),\(BAC\), y\(ACB\)?

    Ejercicio\(\PageIndex{3}\): Every Triangle in the World

    Aquí está\(\Delta ABC\). \(DE\)La línea es paralela a la línea\(AC\).

    clipboard_edfab75957cfe4ba59660eec38fbc5b4f.png
    Figura\(\PageIndex{1}\): El punto B se encuentra en la línea D E. Se dibuja el triángulo B A C. El ángulo A B C está etiquetado como b grados. El ángulo B A C está etiquetado como grados. El ángulo A C B está etiquetado como c grados.
    1. ¿Qué es\(m\angle DBA +b+m\angle CBE\)? Explica cómo sabes.
    2. Usa tu respuesta para explicar por qué\(a+b+c=180\).
    3. Explica por qué tu argumento funcionará para cualquier triángulo: es decir, explica por qué es la suma de las medidas de ángulo en cualquier triángulo\(180^{\circ}\).

    ¿Estás listo para más?

    1. Usando una regla, crea algunos cuadriláteros. Usa un Transportador para medir los cuatro ángulos dentro del cuadrilátero. ¿Cuál es la suma de estas cuatro medidas angulares?
    2. Crea una explicación de por qué cualquier cosa que notes debe ser verdad (pista: dibuja una diagonal en cada cuadrilátero).

    Ejercicio\(\PageIndex{4}\): Four Triangles Revisited

    Este diagrama muestra un cuadrado\(BDFH\) que ha sido realizado por imágenes de triángulo\(ABC\) bajo transformaciones rígidas.

    clipboard_e77f8c0f9d2341758c7da613bd3ea06b7.png
    Figura\(\PageIndex{2}\): Cuadrilátero B D F H. Los ángulos B, D, F y H están marcados como ángulos rectos. El punto C se encuentra en B D. El punto E se encuentra en D F. El punto G se encuentra en F H. El punto A se encuentra en B H. Se dibujan los segmentos A C, C E, E G y G A.

    Dado que el ángulo\(BAC\) mide 53 grados, encuentra tantas otras medidas de ángulo como puedas.

    Resumen

    Usando líneas paralelas y rotaciones, podemos entender por qué los ángulos en un triángulo siempre se suman a\(180^{\circ}\). Aquí está el triángulo\(ABC\). \(DE\)La línea es paralela\(AC\) y contiene\(B\).

    clipboard_edc8064af603b5569fd5469c97d14f8f3.png
    Figura\(\PageIndex{3}\): El punto B se encuentra en el segmento D E. Se dibuja el triángulo B A C. El ángulo D B A está etiquetado x grados. El ángulo A B C está etiquetado como y grados. El ángulo E B C está etiquetado con z grados. El ángulo B A C está etiquetado x grados. El ángulo B C A está etiquetado con z grados.

    Una rotación de 180 grados de triángulo\(ABC\) alrededor del punto medio de\(AB\) intercambia ángulos\(A\) y\(DBA\) así tienen la misma medida: en la imagen estos ángulos están marcados como\(x^{\circ}\). Una rotación de 180 grados del triángulo\(ABC\) alrededor del punto medio de\(BC\) los ángulos de los\(CBE\) intercambios\(C\) y así tienen la misma medida: en la imagen, estos ángulos están marcados como\(z^{\circ}\). También,\(DBE\) es una línea recta porque las rotaciones de 180 grados llevan líneas a líneas paralelas. Entonces los tres ángulos con vértice\(B\) hacen una línea y suman hasta\(180^{\circ}\) (\(x+y+z=180\)). Pero\(x,y,z\) son las medidas de los tres ángulos en\(\Delta ABC\) así la suma de los ángulos en un triángulo es siempre\(180^{\circ}\)!

    Entradas en el glosario

    Definición: Ángulos interiores alternos

    Los ángulos interiores alternos se crean cuando dos líneas paralelas son cruzadas por otra línea llamada transversal. Los ángulos interiores alternos están dentro de las líneas paralelas y en lados opuestos de la transversal.

    Este diagrama muestra dos pares de ángulos interiores alternos. Los ángulos\(a\) y\(d\) son un par y los ángulos\(b\) y\(c\) son otro par.

    clipboard_e4756004d866f53bde0723ab9232e8d0c.png
    Figura\(\PageIndex{4}\): Hay dos líneas paralelas horizontales, y una tercera línea diagonal dibujada desde la parte inferior izquierda hasta la parte superior derecha, intersectando ambas líneas horizontales. La línea diagonal se etiqueta transversal. Hay cuatro ángulos creados por la línea diagonal dentro de las líneas paralelas. El ángulo superior izquierdo está etiquetado como a, superior derecha es b, inferior izquierda es c e inferior derecha es d.

    Definición: Ángulo recto

    Un ángulo recto es un ángulo que forma una línea recta. Mide 180 grados.

    clipboard_e6f095bdb54362766a230a157085a1bed.png
    Figura\(\PageIndex{5}\)

    Definición: Transversal

    Una transversal es una línea que cruza líneas paralelas.

    Este diagrama muestra una línea transversal\(k\) que cruza líneas paralelas\(m\) y\(l\).

    clipboard_ed76014d822bc3ca0adff616e885471aa.png
    Figura\(\PageIndex{6}\)

    Practica

    Ejercicio\(\PageIndex{5}\)

    Para cada triángulo, encuentra la medida del ángulo faltante.

    clipboard_e2552efbadc34b127f315004aed504d3c.png
    La Figura 2 es el triángulo D E F. El ángulo E está etiquetado 122 grados. El ángulo F está etiquetado como 38 grados.

    Ejercicio\(\PageIndex{6}\)

    ¿Hay un triángulo con dos ángulos rectos? Explica tu razonamiento.

    Ejercicio\(\PageIndex{7}\)

    En este diagrama, las líneas\(AB\) y\(CD\) son paralelas.

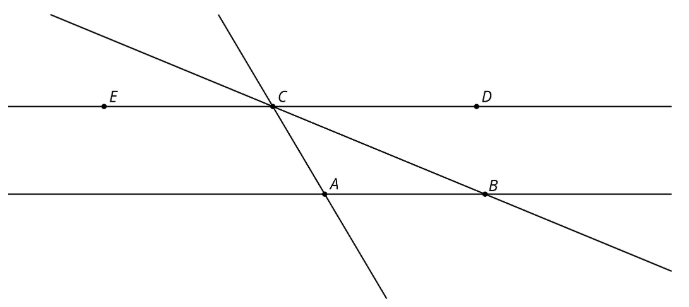
    clipboard_e2cff888493061915da10f38417eccc81.png
    Figura\(\PageIndex{8}\)

    \(ABC\)Medidas de ángulo\(35^{\circ}\) y\(BAC\) medidas de ángulo\(115^{\circ}\).

    1. ¿Qué es\(m\angle ACE\)?
    2. ¿Qué es\(m\angle DCB\)?
    3. ¿Qué es\(m\angle ACB\)?

    Ejercicio\(\PageIndex{8}\)

    Aquí hay un diagrama de triángulo\(DEF\).

    1. Encuentra las medidas de los ángulos\(q\),\(r\), y\(s\).
    2. Encuentra la suma de las medidas de los ángulos\(q\),\(r\), y\(s\).
    3. ¿Qué notas de estos tres ángulos?
    clipboard_eb8d6975a2d4171333687a7bda2c394f3.png
    Figura\(\PageIndex{9}\): Tres líneas se cruzan para formar el Triángulo D E F. El ángulo interior en D está etiquetado 80 grados. El ángulo exterior en D está etiquetado q. El ángulo interior en E está etiquetado 45 grados. El ángulo exterior en E está etiquetado r. El ángulo exterior en F está etiquetado como s.

    Ejercicio\(\PageIndex{9}\)

    Las dos cifras son congruentes.

    1. Etiquetar los puntos\(A'\)\(B'\),, y\(C'\) que corresponden a\(A\),\(B\), y\(C\) en la figura de la derecha.

    clipboard_ee99b3cb920822ae6aefa38be45e81f23.png
    Figura\(\PageIndex{10}\): Dos figuras congruentes son semicírculos con un punto de ángulo opuesto conectado. La figura izquierda tiene el punto A en el punto de ángulo inferior, el punto B en el lado derecho donde se encuentran el semicírculo y el segmento AB y el punto C en el punto medio del semicírculo superior. La figura derecha tiene el semicírculo en la parte inferior con un punto en el punto medio, un punto en el lado izquierdo donde se encuentran el semicírculo y el segmento y un punto en el punto de ángulo superior.

    2. Si el segmento\(AB\) mide 2 cm, ¿cuánto tiempo es el segmento\(A'B'\)? Explique.

    3. El punto\(D\) se muestra además de\(A\) y\(C\). ¿Cómo puedes encontrar el punto\(D'\) que corresponde\(D\)? Explica tu razonamiento.

    clipboard_ed039ff4ab9ea12af301d012288d38cdc.png
    Figura\(\PageIndex{11}\): Dos figuras congruentes son semicírculos con un punto de ángulo opuesto conectado. La figura izquierda tiene el punto A en el punto de ángulo inferior, el punto D en el lado izquierdo por debajo donde se encuentran el semicírculo y el segmento AB y el punto C en el punto medio del semicírculo superior. La figura derecha tiene el semicírculo en la parte inferior con un punto en el punto medio, y un punto en el punto de ángulo superior.

    (De la Unidad 1.3.3)

    This page titled 1.4.3: Líneas paralelas y los ángulos en un triángulo is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.