2.1.5: Más dilataciones
- Page ID
- 118651
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Veamos las dilataciones en el plano de coordenadas.
Ejercicio\(\PageIndex{1}\): Many Dilations of a Triangle
Explora el applet y observa la dilatación del triángulo\(ABC\). La dilatación siempre usa centro\(P\), pero se puede cambiar el factor de escala. ¿Qué conexiones puedes hacer entre el factor de escala y el triángulo dilatado?
Ejercicio\(\PageIndex{2}\): Info Gap: Dilations
Tu profesor te dará ya sea una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu pareja.
Si tu profesor te da la tarjeta de problemas:
- Lee silenciosamente tu tarjeta y piensa en qué información necesitas para poder responder a la pregunta.
- Pídele a tu pareja la información específica que necesites.
- Explique cómo está utilizando la información para resolver el problema.
- Continúa haciendo preguntas hasta que tengas la información suficiente para resolver el problema.
- Comparte la tarjeta de problemas y resuelve el problema de forma independiente.
- Lee la tarjeta de datos y discute tu razonamiento.
Si tu profesor te da la tarjeta de datos:
- Lee silenciosamente tu tarjeta.
- Pregúntale a tu pareja “¿Qué información específica necesitas?” y esperar a que pidan información.
Si tu pareja solicita información que no esté en la tarjeta, no hagas los cálculos por ellos. Diles que no tienes esa información.
- Antes de compartir la información, pregunta “¿Por qué necesitas esa información? ” Escucha el razonamiento de tu pareja y haz preguntas aclaratorias.
- Lea la tarjeta del problema y resuelva el problema de forma independiente.
- Comparte la tarjeta de datos y discute tu razonamiento.
Haz una pausa aquí para que tu profesor pueda revisar tu trabajo. Pídele a tu profesor un nuevo juego de cartas y repite la actividad, negociando roles con tu pareja.
¿Estás listo para más?
\(EFG\)El triángulo se creó dilatando el triángulo\(ABC\) usando un factor de escala de 2 y centro\(D\). \(HIJ\)El triángulo se creó dilatando el triángulo\(ABC\) usando un factor de escala de\(\frac{1}{2}\) y centro\(D\).
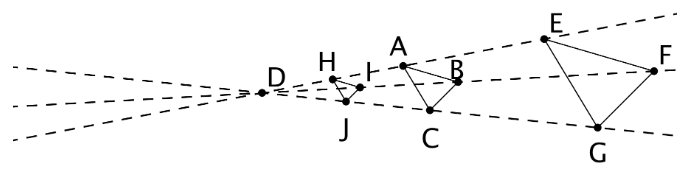
- ¿Cómo sería la imagen del triángulo\(ABC\) bajo una dilatación con factor de escala 0?
- ¿Cómo sería la imagen del triángulo bajo dilatación con un factor de escala de -1? Si es posible, dibuje y etiquete los vértices\(A'\),\(B'\), y\(C'\). Si no es posible, explique por qué no.
- Si es posible, describa lo que le sucede a una forma si se dilata con un factor de escala negativo. Si no es posible dilatar con un factor de escala negativo, explique por qué no.
Resumen
Un uso importante de las coordenadas es comunicar información geométrica con precisión. Consideremos un cuadrilátero\(ABCD\) en el plano de coordenadas. Realizar una dilatación de\(ABCD\) requiere tres piezas vitales de información:
- Las coordenadas de\(A\),\(B\),\(C\), y\(D\)
- Las coordenadas del centro de dilatación,\(P\)
- El factor de escala de la dilatación
Con esta información, podemos dilatar los vértices\(A\),\(B\),\(C\),\(D\) y luego dibujar los segmentos correspondientes para encontrar la dilatación de\(ABCD\). Sin coordenadas, describir la ubicación de los nuevos puntos probablemente requeriría compartir una imagen del polígono y el centro de dilatación.
Entradas en el glosario
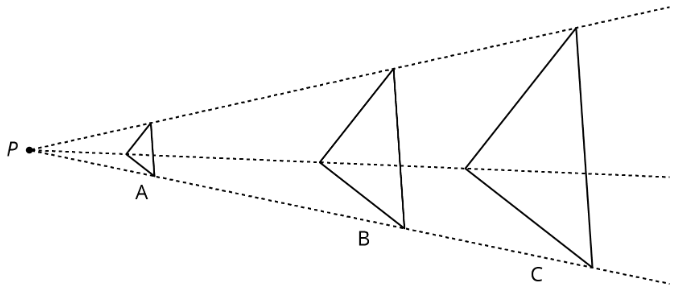
Definición: Centro de una Dilatación
El centro de una dilatación es un punto fijo en un plano. Es el punto de partida desde el que medimos distancias en una dilatación.
En este diagrama, el punto\(P\) es el centro de la dilatación.
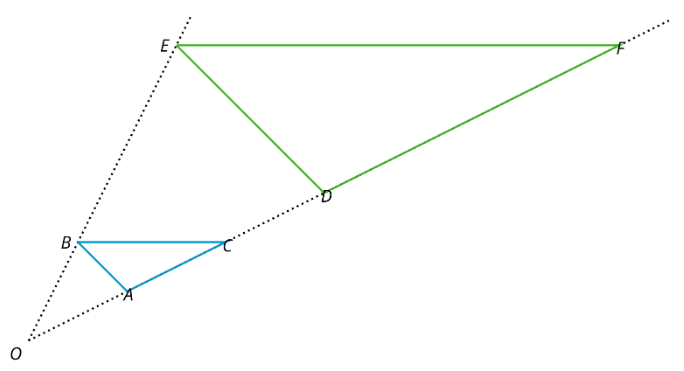
Definición: Dilatación
Una dilatación es una transformación en la que cada punto de una figura se mueve a lo largo de una línea y cambia su distancia desde un punto fijo. El punto fijo es el centro de la dilatación. Todas las distancias originales se multiplican por el mismo factor de escala.
Por ejemplo, triángulo\(DEF\) es una dilatación de triángulo\(ABC\). El centro de dilatación es\(O\) y el factor de escala es 3.
Esto significa que cada punto del triángulo\(DEF\) está 3 veces más lejos\(O\) de cada punto correspondiente del triángulo\(ABC\).
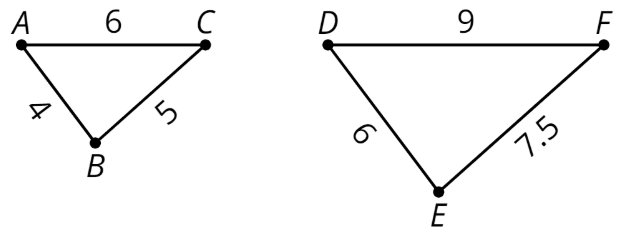
Definición: Factor de Escala
Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. Este número se llama factor de escala.
En este ejemplo, el factor de escala es 1.5, porque\(4\cdot (1.5)=6\),\(5\cdot (1.5)=7.5\), y\(6\cdot (1.5)=9\).
Practica
Ejercicio\(\PageIndex{3}\)
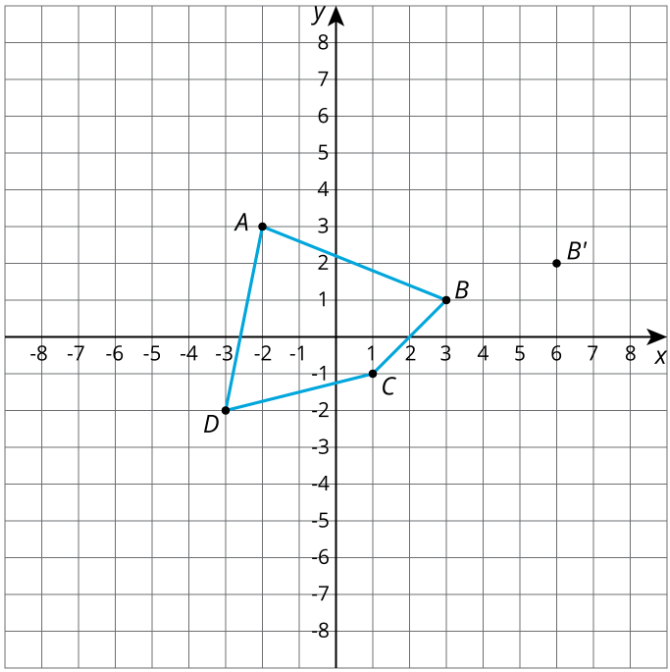
El cuadrilátero\(ABCD\) se dilata con centro\((0,0)\) llevando\(B\) a\(B'\). Empate\(A'B'C'D'\).
Ejercicio\(\PageIndex{4}\)
Triángulos\(B\) y se\(C\) han construido dilatando Triángulo\(A\).
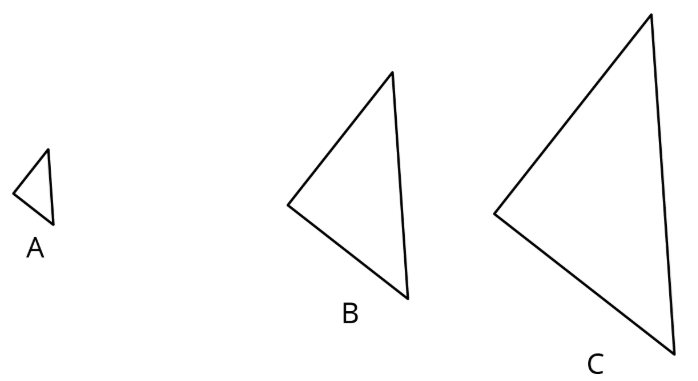
- Encuentra el centro de dilatación.
- Triángulo\(B\) es una dilatación de\(A\) aproximadamente ¿qué factor de escala?
- Triángulo\(A\) es una dilatación de\(B\) aproximadamente ¿qué factor de escala?
- Triángulo\(B\) es una dilatación de\(C\) aproximadamente ¿qué factor de escala?
Ejercicio\(\PageIndex{5}\)
Aquí hay un triángulo.
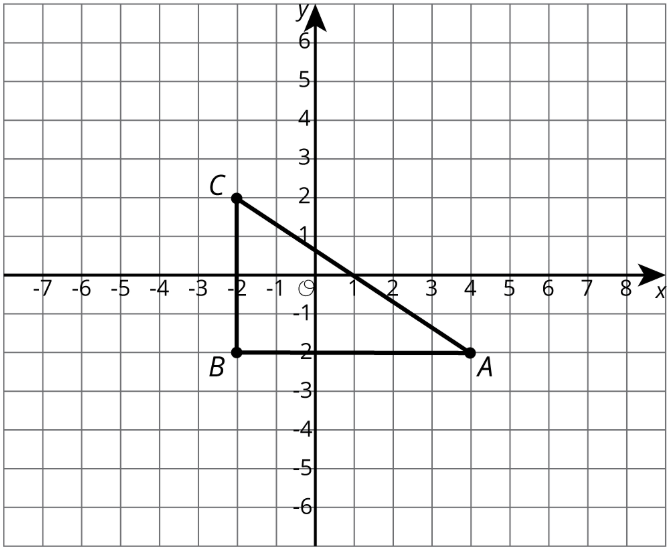
- Dibuja la dilatación del triángulo\(ABC\), con centro\((0,0)\), y factor de escala 2. Etiquete este triángulo\(A'B'C'\).
- Dibuja la dilatación del triángulo\(ABC\), con centro\((0,0)\) y factor de escala\(\frac{1}{2}\). Etiquete este triángulo\(A''B''C''\).
- ¿Es\(A''B''C''\) una dilatación de triángulo\(A'B'C'\)? En caso afirmativo, ¿cuáles son el centro de dilatación y el factor de escala?
Ejercicio\(\PageIndex{1}\)
\(DEF\)El triángulo es un triángulo rectángulo, y la medida del ángulo\(D\) es\(28^{\circ}\). ¿Cuáles son las medidas de los otros dos ángulos?
(De la Unidad 1.4.2)