2.1.4: Dilataciones en una Rejilla Cuadrada
- Page ID
- 118647
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Vamos a dilatar figuras en una cuadrícula cuadrada.
Ejercicio\(\PageIndex{1}\): Estimating a Scale Factor
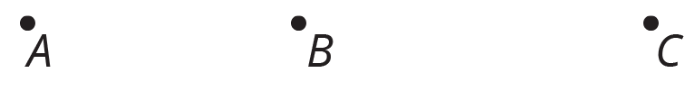
Punto\(C\) es la dilatación del punto\(B\) con centro de dilatación y factor de escala. Estimar. Esté preparado para explicar su razonamiento.
Ejercicio\(\PageIndex{2}\): Dilations on a Grid
1. Encuentra la dilatación del cuadrilátero\(ABCD\) con centro\(P\) y factor de escala 2.
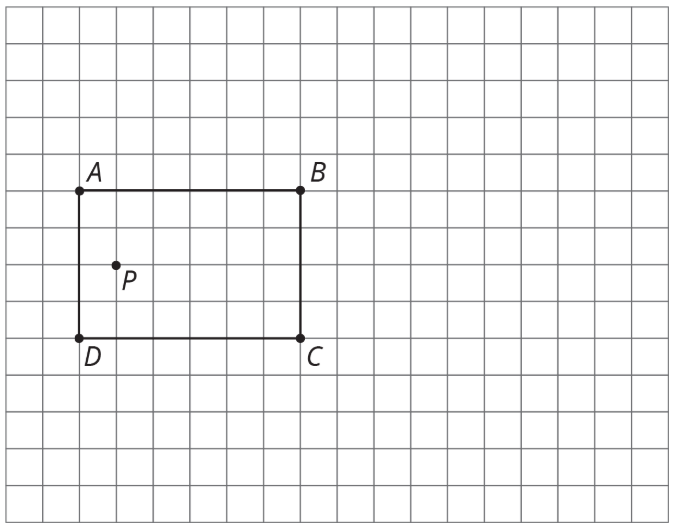
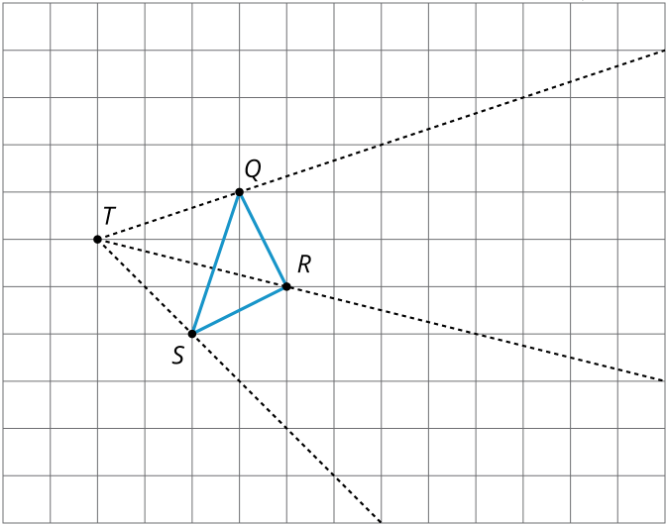
2. Encuentra la dilatación del triángulo\(QRS\) con centro\(T\) y factor de escala\(2\).
3. Encuentra la dilatación del triángulo\(QRS\) con centro\(T\) y factor de escala\(\frac{1}{2}\).
Ejercicio\(\PageIndex{3}\): Card Sort: Matching Dilations on a Coordinate Grid
Tu profesor te dará algunas tarjetas. Cada una de las Cartas 1 a 6 muestra una figura en el plano de coordenadas y describe una dilatación.
Cada una de las Cartas A a E describe la imagen de la dilatación de una de las tarjetas numeradas.
Coinciden tarjetas de números con tarjetas de letras. Una de las tarjetas numéricos no tendrá coincidencia. Para esta tarjeta, necesitarás dibujar una imagen.
¿Estás listo para más?
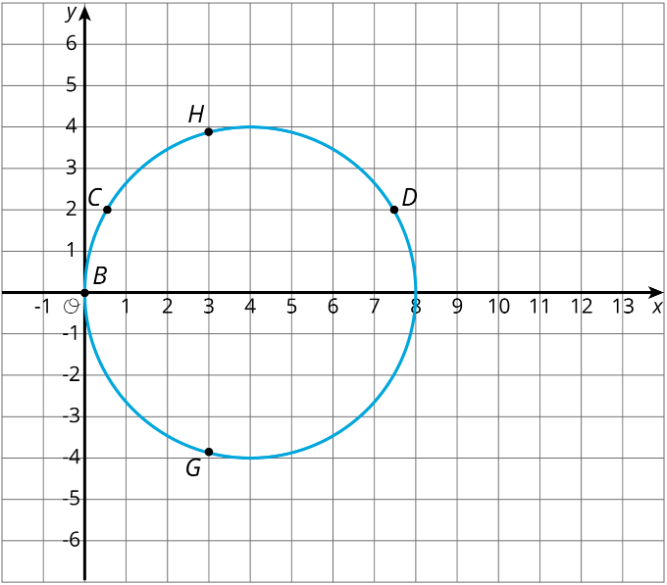
La imagen de un círculo bajo dilatación es un círculo cuando el centro de la dilatación es el centro del círculo. ¿Qué pasa si el centro de dilatación es un punto en el círculo? Utilizando el centro de dilatación\((0,0)\) y factor de escala 1.5, dilatar el círculo que se muestra en el diagrama. Este diagrama muestra algunos puntos para intentar dilatar.
Resumen
Las cuadrículas cuadradas pueden ser útiles para mostrar dilataciones. La cuadrícula es útil especialmente cuando el centro de dilatación y los puntos que se dilatan se encuentran en los puntos de la cuadrícula. En lugar de usar una regla para medir la distancia entre los puntos, podemos contar unidades de cuadrícula.
Por ejemplo, supongamos que queremos dilatar punto\(Q\) con centro de dilatación\(P\) y factor de escala\(\frac{3}{2}\). Dado que\(Q\) es 4 cuadrados de cuadrícula a la izquierda y 2 cuadrados de cuadrícula hacia abajo de\(P\), la dilatación será de 6 cuadrados de cuadrícula a la izquierda y 3 cuadrados de cuadrícula hacia abajo de\(P'\) (¿ves por qué?). La imagen dilatada se marca como\(Q'\) en la imagen.
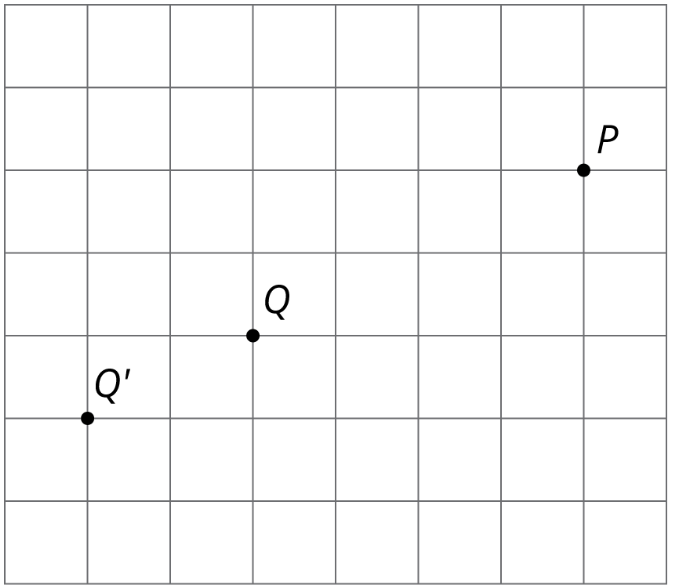
A veces la cuadrícula cuadrada viene con coordenadas. La cuadrícula de coordenadas nos da una manera conveniente de nombrar puntos, y en ocasiones las coordenadas de la imagen se pueden encontrar con solo aritmética.
Por ejemplo, para hacer una dilatación con centro\((0,0)\) y factor de escala 2 del triángulo con coordenadas\((-1,-2)\),\((3,1)\), y\((2,-1)\), podemos simplemente duplicar las coordenadas para obtener\((-2,-4)\),\((6,2)\), y\((4,-2)\).
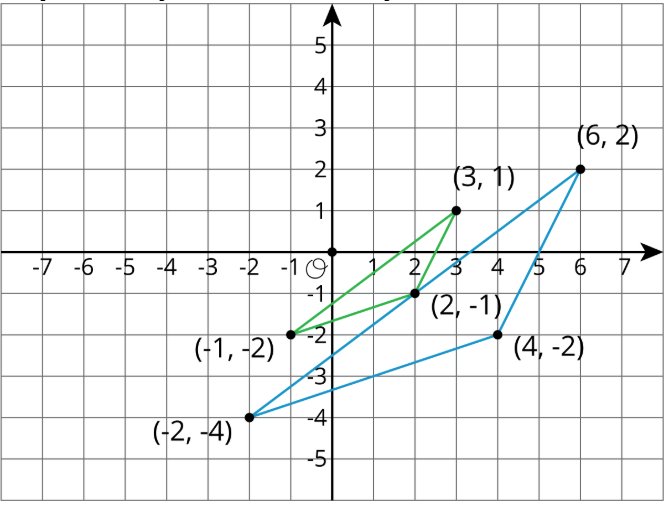
Glosario
Definición: Centro de una Dilatación
El centro de una dilatación es un punto fijo en un plano. Es el punto de partida desde el que medimos distancias en una dilatación.
En este diagrama, el punto\(P\) es el centro de la dilatación.
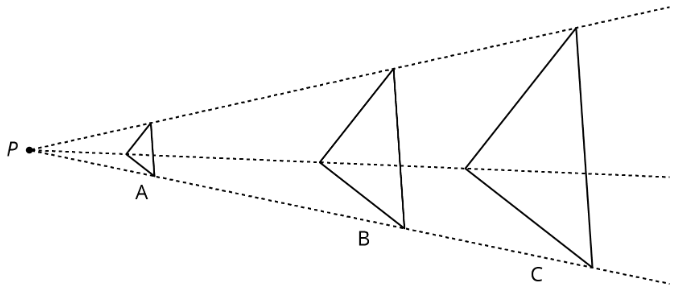
Definición: Dilatación
Una dilatación es una transformación en la que cada punto de una figura se mueve a lo largo de una línea y cambia su distancia desde un punto fijo. El punto fijo es el centro de la dilatación. Todas las distancias originales se multiplican por el mismo factor de escala.
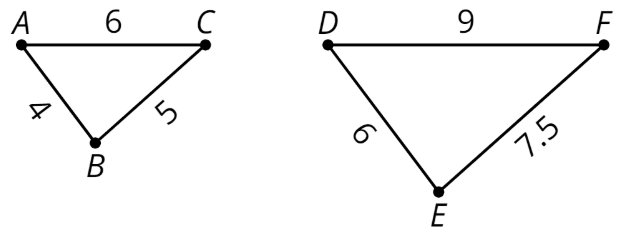
Por ejemplo, triángulo\(DEF\) es una dilatación de triángulo\(ABC\). El centro de dilatación es\(O\) y el factor de escala es 3.
Esto significa que cada punto del triángulo\(DEF\) está 3 veces más lejos\(O\) de cada punto correspondiente del triángulo\(ABC\).
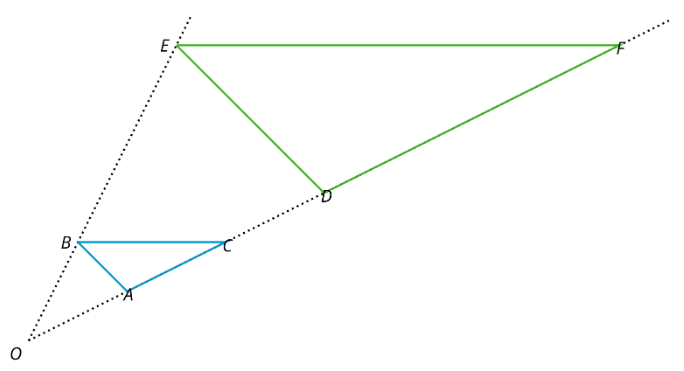
Definición: Factor de Escala
Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. A este número se le llama factor de escala.
En este ejemplo, el factor de escala es 1.5, porque\(4\cdot (1.5)=6\),\(5\cdot (1.5)=7.5\), y\(6\cdot (1.5)=9\).
Practica
Ejercicio\(\PageIndex{4}\)
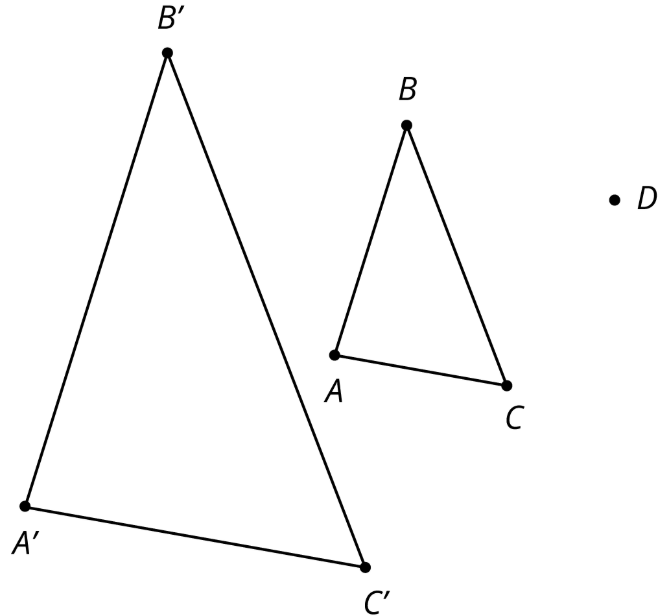
\(ABC\)El triángulo se dilata usando\(D\) como centro de dilatación con factor de escala\(2\).
La imagen es triángulo\(A'B'C'\). Clare dice que los dos triángulos son congruentes, porque sus medidas angulares son las mismas. ¿Estás de acuerdo? Explique cómo sabe.
Ejercicio\(\PageIndex{5}\)
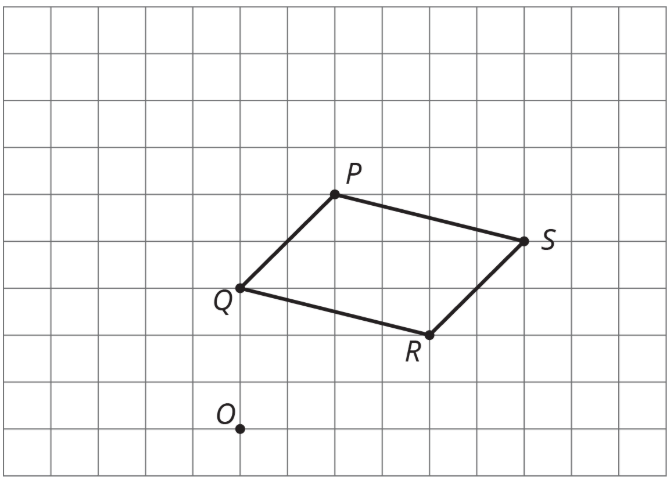
En papel cuadriculado, dibuje la imagen del PQRS cuadrilátero bajo las siguientes dilataciones:
- La dilatación se centró en\(R\) con factor de escala\(2\).
- La dilatación se centró en\(O\) con factor de escala\(\frac{1}{2}\).
- La dilatación se centró en\(S\) con factor de escala\(\frac{1}{2}\).
Ejercicio\(\PageIndex{6}\)
El diagrama muestra tres líneas con algunas medidas de ángulo marcadas.
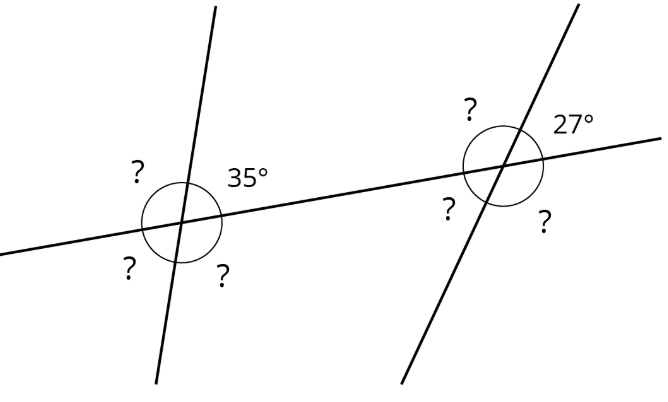
Una línea inclinada hacia arriba y hacia la derecha. Dos líneas se cruzan con esta línea, ambas inclinadas hacia arriba y hacia la derecha, pero no se cruzan. En la primera intersección, el ángulo superior derecho se etiqueta 35 grados. El resto están etiquetados?. En la segunda intersección, el ángulo superior derecho está etiquetado como 27 grados. El resto están etiquetados?.
Encuentra las medidas de ángulo faltantes marcadas con signos de interrogación.
(De la Unidad 1.4.4)
Ejercicio\(\PageIndex{7}\)
Describir una secuencia de traslaciones, rotaciones y reflexiones que llevan el Polígono P al Polígono Q.
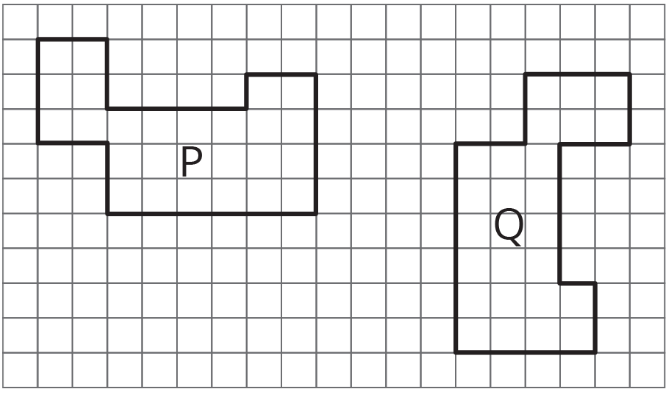
(De la Unidad 1.1.4)
Ejercicio\(\PageIndex{8}\)
\(B\)El punto tiene coordenadas\((-2,-5)\). Después de una traslación 4 unidades hacia abajo, una reflexión a través del eje, y una traslación 6 unidades hacia arriba, ¿cuáles son las coordenadas de la imagen?
(De la Unidad 1.1.6)