2.2.1: Similitud

Última actualización
Guardar como PDF

Page ID: 118662

Illustrative Mathematics
OpenUp Resources

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lección

Exploremos figuras similares.

Ejercicio\(\PageIndex{1}\): Equivalent Expressions

Usa lo que sabes sobre las operaciones y sus propiedades para escribir tres expresiones equivalentes a la expresión mostrada.

\(10(2+3)-8\cdot 3\)

Ejercicio\(\PageIndex{2}\): Similarity Transformations (Part 1)

1. Triángulo\(EGH\) y triángulo\(LME\) son similares. Encuentra una secuencia de tansolaciones, rotaciones, reflejos y dilataciones que lo demuestre.

2. Hexágono\(ABCDEF\) y hexágono\(HGLKJI\) son similares. Encuentra una secuencia de traslaciones, rotaciones, reflexiones y dilataciones que lo demuestre.

¿Estás listo para más?

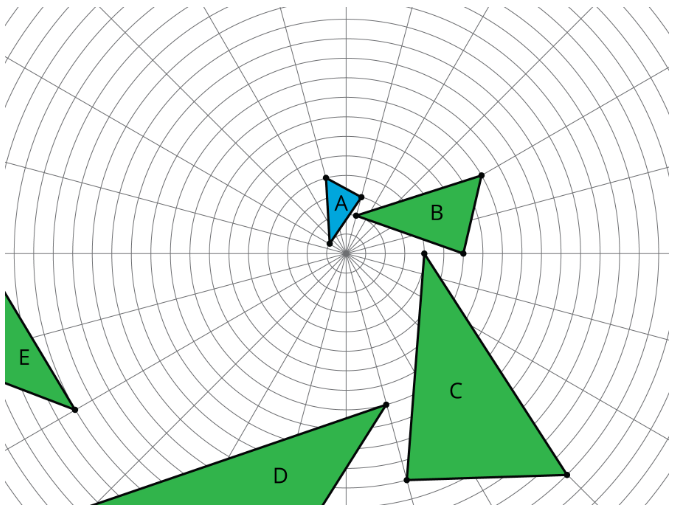
La misma secuencia de transformaciones lleva el Triángulo A al Triángulo B, toma el Triángulo B al Triángulo C, y así sucesivamente. Describir una secuencia de transformaciones con esta propiedad.

Ejercicio\(\PageIndex{3}\): Similarity Transformations (Part 2)

Esboce figuras similares a la Figura A que utilizan únicamente las transformaciones listadas para mostrar similitud.

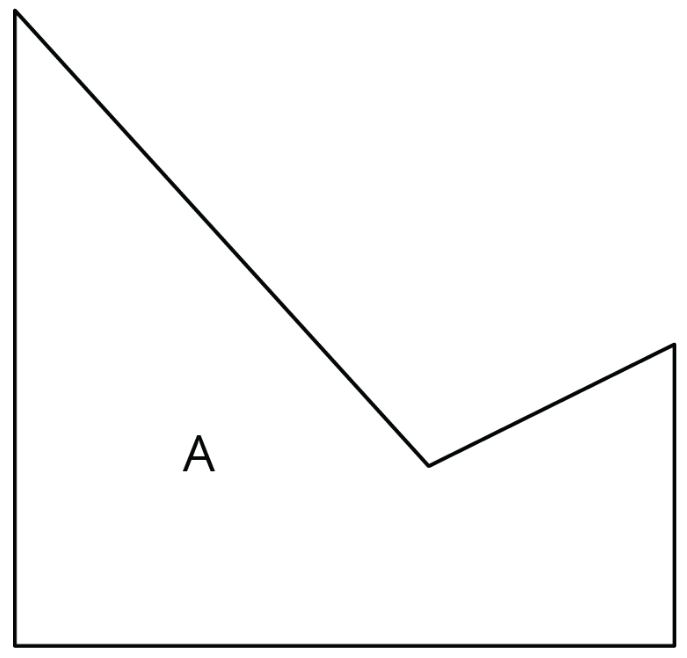
Una traducción y una reflexión. Etiquete su boceto Figura B.
Haga una pausa aquí para que su profesor pueda revisar su trabajo.
Una reflexión y una dilatación con factor de escala mayor a 1. Etiquete su boceto Figura C.
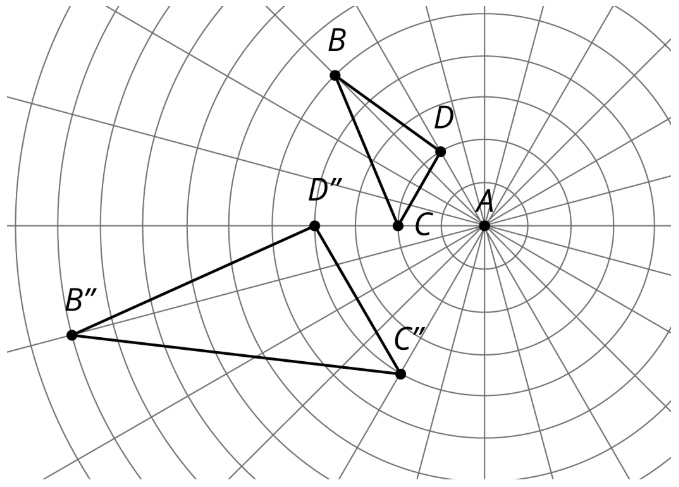
Una rotación y una reflexión. Etiquete su boceto Figura D.
Una dilatación con factor de escala menor a 1 y una traslación. Etiquete su boceto Figura E.

Ejercicio\(\PageIndex{4}\): Methods for Translations and Dilations

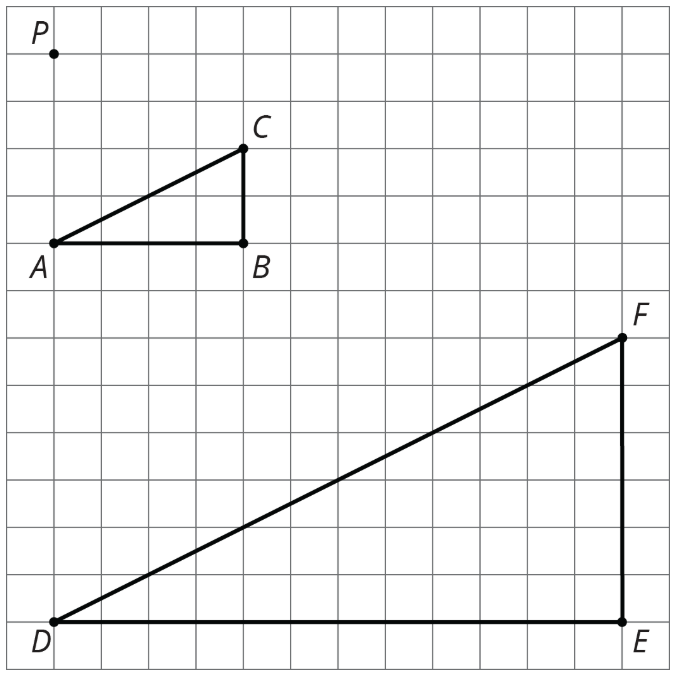
Tu profesor te dará un juego de cinco cartas y a tu pareja un juego diferente de cinco cartas. Usando solo las cartas que te dieron, encuentra al menos una manera de mostrar que el triángulo\(ABC\) y el triángulo\(DEF\) son similares. Compara tu método con el método de tu pareja. ¿Qué es lo mismo de tus métodos? ¿Qué es diferente?

Resumen

Demostremos que el triángulo\(ABC\) es similar al triángulo\(DEF\):

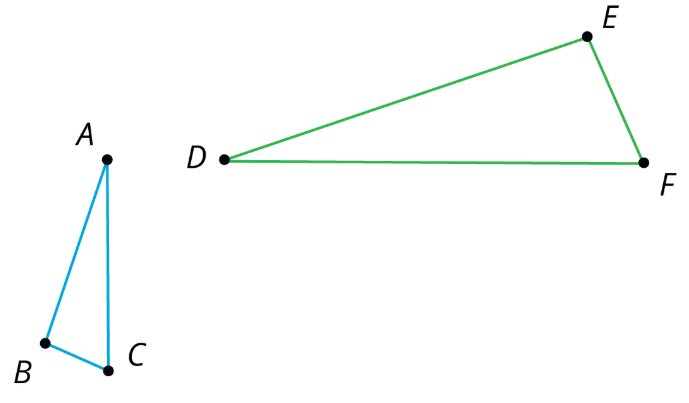
Dos figuras son similares si una figura se puede transformar en la otra mediante una secuencia de traslaciones, rotaciones, reflexiones y dilataciones. Hay muchas secuencias correctas de transformaciones, pero solo necesitamos describir una para mostrar que dos figuras son similares.

Una forma de llegar de\(ABC\) a\(DEF\) sigue estos pasos:

paso 1: reflejar a través de la línea\(f\)
paso 2: girar en\(90^{\circ}\) sentido antihorario alrededor\(D\)
paso 3: dilatar con centro\(D\) y factor de escala 2

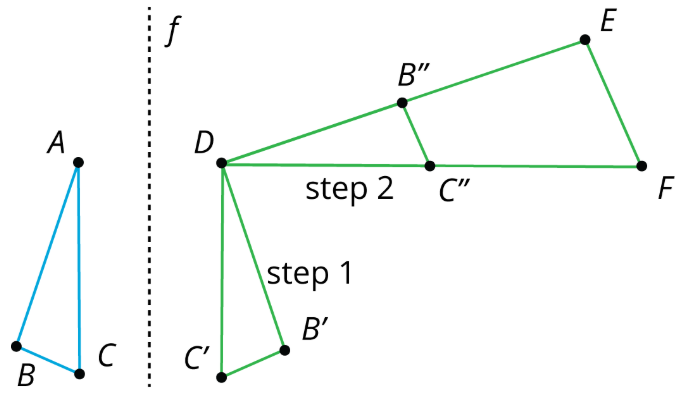
Otra forma sería dilatar el triángulo\(ABC\) por un factor de escala de 2 con centro de dilatación\(A\), luego traducirlo\(A\) a\(D\), luego reflexionar sobre una línea vertical a través\(D\), y finalmente girarlo para que coincida con el triángulo\(DEF\). ¿Qué pasos elegirías para mostrar que los dos triángulos son similares?

Entradas en el glosario

Definición: Similar

Dos figuras son similares si una puede encajar exactamente sobre la otra después de transformaciones rígidas y dilataciones.

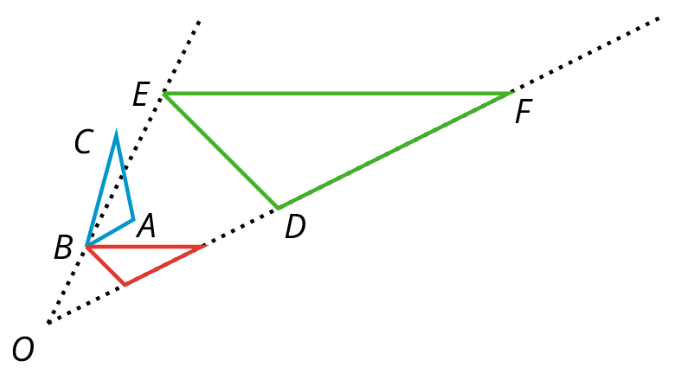
En esta figura, el triángulo\(ABC\) es similar al triángulo\(DEF\).

Si\(ABC\) se gira alrededor del punto\(B\) y luego se dilata con el punto central\(O\), entonces se ajustará exactamente sobre\(DEF\). Esto quiere decir que son similares.

Practica

Ejercicio\(\PageIndex{5}\)

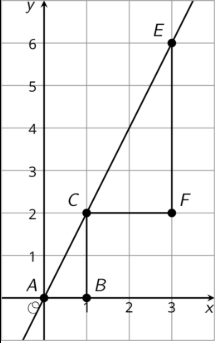
Cada diagrama tiene un par de figuras, una más grande que la otra. Para cada par, mostrar que las dos figuras son similares al identificar una secuencia de traslaciones, rotaciones, reflexiones y dilataciones que lleva la figura más pequeña a la más grande.

Ejercicio\(\PageIndex{6}\)

Aquí hay dos polígonos similares.

Figura\(\PageIndex{9}\): figura ABCD y figura EFGH sobre una cuadrícula de 10 por 10. dejando esquina inferior izquierda = 0 coma 0, A = 1 coma 9, B = 1 coma 6, C = 3 coma 5, D = 2 coma 6, E = 9 coma 9, F = 9 coma 3, G = 5 coma 1, H = 7 coma 3.

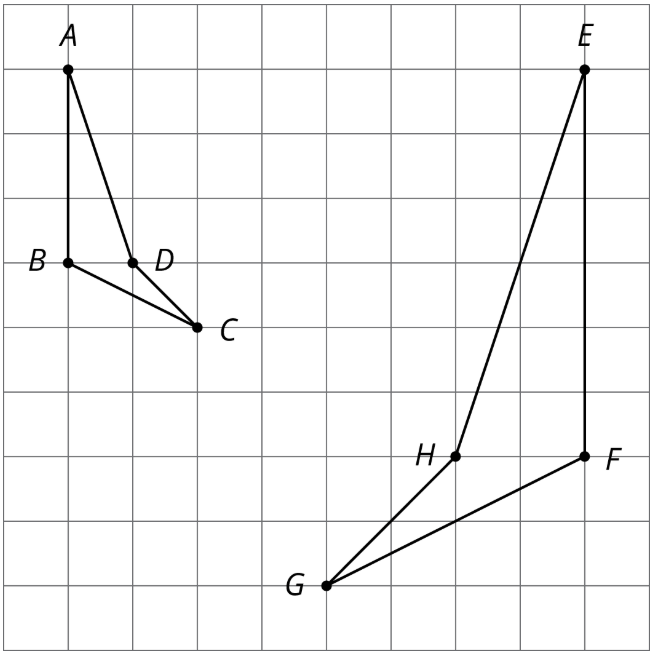
Mida las longitudes y ángulos laterales de cada polígono. ¿Qué notas?

Ejercicio\(\PageIndex{7}\)

Cada figura muestra un par de triángulos similares, uno contenido en el otro. Para cada par, describa un punto y un factor de escala para usar para una dilatación moviendo el triángulo más grande al más pequeño. Utilice una herramienta de medición para encontrar el factor de escala.