Saltar al contenido principal
LibreTexts Español

2.2.2: Polígonos similares

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118663

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Veamos los lados y ángulos de polígonos similares

    Ejercicio\(\PageIndex{1}\): All, Some, None: Congruence and Similarity

    Elegir si cada una de las afirmaciones es verdadera en todos los casos, en algunos casos, o en ningún caso.

    1. Si dos figuras son congruentes, entonces son similares.
    2. Si dos figuras son similares, entonces son congruentes.
    3. Si se dilata un ángulo con el centro de dilatación en su vértice, la medida del ángulo puede cambiar.

    Ejercicio\(\PageIndex{2}\): Are They Similar?

    1.

    clipboard_e4e66be0584dccf56bbcaf51605c681e5.png
    Figura\(\PageIndex{1}\)

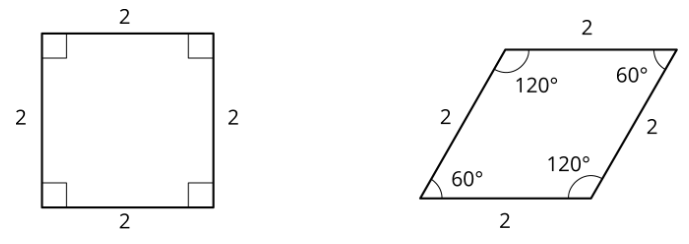
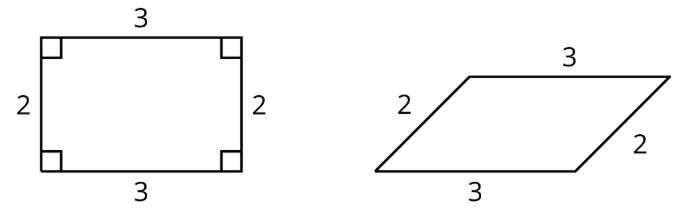
    Veamos un cuadrado y un rombo.

    Priya dice: “Estos polígonos son similares porque sus longitudes laterales son todas iguales”. Clare dice: “Estos polígonos no son similares porque los ángulos son diferentes”. ¿Estás de acuerdo con Priya o con Clare? Explica tu razonamiento.

    2. Ahora veamos rectángulos\(ABCD\) y\(EFGH\).

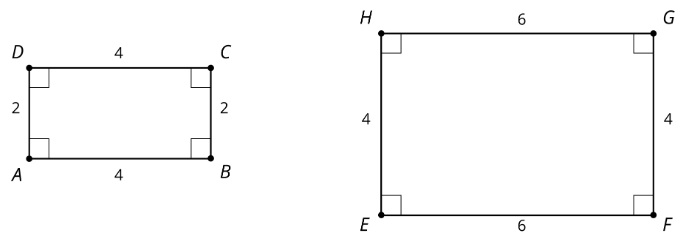
    clipboard_ed303c6ab25fb67d0c80d10b1cd79e00a.png
    Figura\(\PageIndex{2}\)

    Jada dice: “Estos rectángulos son similares porque todas las longitudes de los lados difieren en 2”. Lin dice: “Estos rectángulos son similares. Puedo dilatar\(AD\) y\(BC\) usando un factor de escala de 2 y\(AB\) y\(CD\) usando un factor de escala de 1.5 para hacer congruentes los rectángulos. Entonces puedo usar una traducción para alinear los rectángulos”. ¿Estás de acuerdo con Jada o Lin? Explica tu razonamiento.

    ¿Estás listo para más?

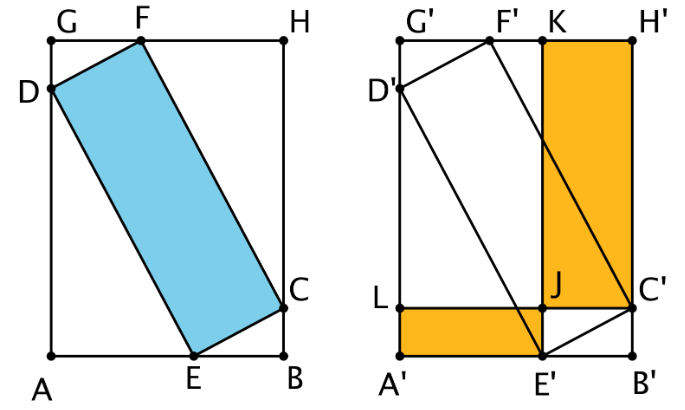
    clipboard_e0d473cd7d09edf2e790ac6b4bce2a923.png
    Figura\(\PageIndex{3}\): Un rectángulo está formado por los lados G F H y H C B y B E A y A D G. El cuadrilátero F C E D también es un rectángulo. La forma se traduce directamente a los puntos A, primo a H primo. K se encuentra entre F primo y H primo. J se posiciona para formar el rectángulo K H primo C primo J y el rectángulo J E primo A, primo L donde L se encuentra entre D primo y A primo.

    Los puntos\(A\) a través\(H\) se traducen a la derecha para crear puntos\(A'\) a través\(H'\). Todos los siguientes son rectángulos:\(GHBA\),\(FCED\),\(KH'C'J\), y\(LJE'A'\). ¿Cuál es mayor, el área de rectángulo azul\(DFCE\) o el área total de rectángulos amarillos\(KH'C'J\) y\(LJE'A'\)?

    Ejercicio\(\PageIndex{3}\): Find Someone Similar

    Tu profesor te dará una tarjeta. Encuentra a alguien más en la habitación que tenga una tarjeta con un polígono que sea similar pero no congruente al tuyo. Cuando hayas encontrado a tu pareja, trabaja con ellos para explicarte cómo sabes que los dos polígonos son similares.

    ¿Estás listo para más?

    A la izquierda hay un triángulo equilátero donde se han agregado líneas discontinuas, mostrando cómo se puede dividir un triángulo equilátero en triángulos similares más pequeños.

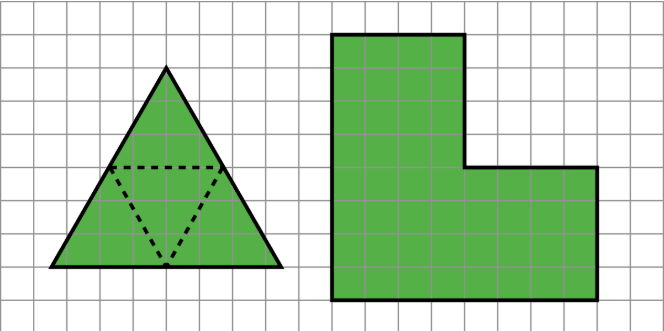
    clipboard_eb96c600443653ce5f76672c201a27dc3.png
    Figura\(\PageIndex{4}\): Dos figuras en una cuadrícula. Primero, un triángulo equilátero una línea punteada a medio camino entre la base y el vértice superior paralelo a la base. Las líneas punteadas conectan cada extremo de la primera línea punteada con el centro de la base. Segundo, una forma de L formada tomando un cuadrado con 8 unidades a cada lado y retirando un cuadrado de 4 por 4 de la esquina superior derecha.

    Encuentra la manera de hacerlo para la figura de la derecha, dividiéndola en figuras más pequeñas que son cada una similar a esa forma original. ¿Cuál es la menor cantidad de piezas que puedes usar? ¿El más?

    Resumen

    Cuando dos polígonos son similares:

    • Cada ángulo y cada lado de un polígono tiene una parte correspondiente en el otro polígono.
    • Todos los pares de ángulos correspondientes tienen la misma medida.
    • Los lados correspondientes están relacionados por un solo factor de escala. Cada longitud de lado en una figura se multiplica por el factor de escala para obtener la longitud lateral correspondiente en la otra figura.

    Considera los dos rectángulos que se muestran aquí. ¿Son similares?

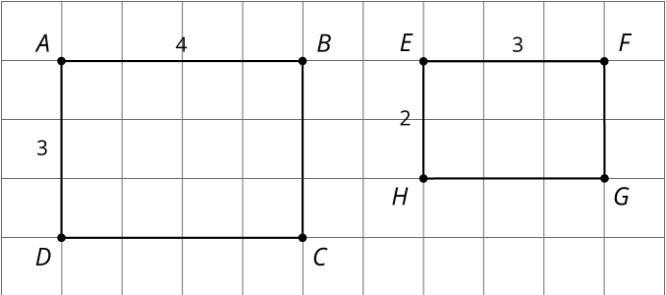
    clipboard_eb4c9d605dce6fb82408fca5ad3c3375f.png
    Figura\(\PageIndex{5}\)

    Parece rectángulos\(ABCD\) y\(EFGH\) podría ser similar, si coincide con los bordes largos y coincide con los bordes cortos. Todos los ángulos correspondientes son congruentes porque todos son ángulos rectos. Calcular el factor de escala entre los lados es donde vemos que “parece” no es suficiente para hacerlos similares. Para escalar el lado largo\(AB\) al lado largo\(EF\), el factor de escala debe ser\(\frac{3}{4}\), porque\(4\cdot\frac{3}{4}=3\). Pero el factor de escala a\(AD\) igualar\(EH\) tiene que ser\(\frac{2}{3}\), porque\(3\cdot\frac{2}{3}=2\). Entonces, los rectángulos no son similares porque los factores de escala para todas las partes deben ser los mismos.

    Aquí hay un ejemplo que muestra cómo los lados pueden corresponder (con un factor de escala de 1), pero los cuadriláteros no son similares porque los ángulos no tienen la misma medida:

    clipboard_e406bb5728ca5dad05aceea570a1a8db7.png
    Figura\(\PageIndex{6}\)

    Entradas en el glosario

    Definición: Similar

    Dos figuras son similares si una puede encajar exactamente sobre la otra después de transformaciones rígidas y dilataciones.

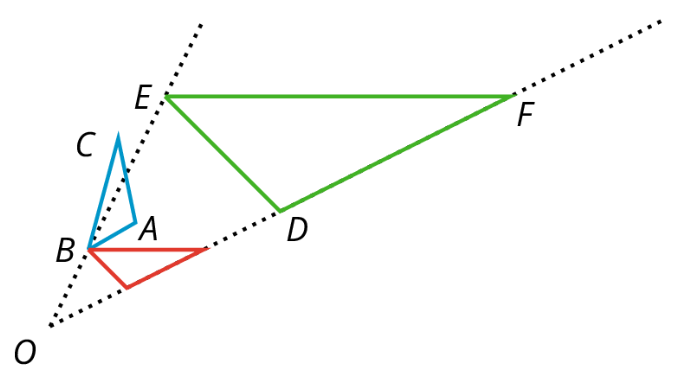
    En esta figura, el triángulo\(ABC\) es similar al triángulo\(DEF\).

    Si\(ABC\) se gira alrededor del punto\(B\) y luego se dilata con el punto central\(O\), entonces se ajustará exactamente sobre\(DEF\). Esto quiere decir que son similares.

    clipboard_efee2a9891ee931c63c0efd5493d1589b.png
    Figura\(\PageIndex{7}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    Triángulo\(DEF\) es una dilatación de triángulo\(ABC\) con factor de escala 2. En triángulo\(ABC\), el ángulo más grande mide\(82^{\circ}\). ¿Cuál es la medida de ángulo más grande en triángulo\(DEF\)?

    1. \(41^{\circ}\)
    2. \(82^{\circ}\)
    3. \(123^{\circ}\)
    4. \(164^{\circ}\)

    Ejercicio\(\PageIndex{5}\)

    Dibuja dos polígonos que son similares pero que podrían confundirse con no ser similares. Explique por qué son similares.

    Ejercicio\(\PageIndex{6}\)

    Dibuja dos polígonos que no sean similares pero que podrían confundirse con ser similares. Explique por qué no son similares.

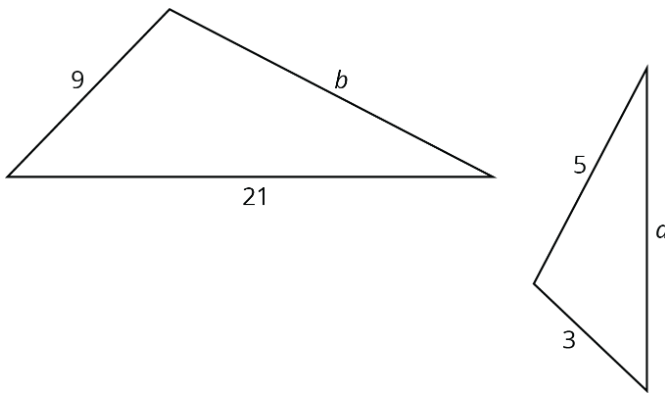
    Ejercicio\(\PageIndex{7}\)

    Estos dos triángulos son similares. Encuentra longitudes laterales\(a\) y\(b\). Nota: las dos figuras no están dibujadas a escala.

    clipboard_e6b562e598dd150b7562d17c132c7d8dc.png
    Figura\(\PageIndex{8}\)

    Ejercicio\(\PageIndex{8}\)

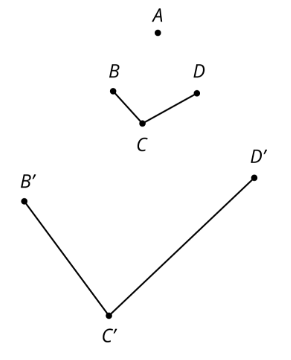
    Jada afirma que\(B'C'D'\) es una dilatación de\(BCD\) usar\(A\) como centro de dilatación.

    ¿Cuáles son algunas formas en las que puedes convencer a Jada de que su afirmación no es cierta?

    clipboard_ed7adad9dfb01e63e7999fe07525ad02e.png
    Figura\(\PageIndex{9}\): Punto A, ángulo B C D e imagen de ángulo B prima, C prima, D prima. El punto A está por encima, luego B C D y debajo de todo es B primo C primo D primo. B C D es más pequeño y parece ser obtuso. B primo C primo D primo es tres veces más grande y parece tener razón.

    (De la Unidad 2.1.3)

    Ejercicio\(\PageIndex{9}\)

    1. Dibuja un segmento de línea horizontal\(AB\).
    2. Gire el segmento hacia la\(AB 90^{\circ}\) izquierda alrededor del punto\(A\). Etiquetar cualquier punto nuevo.
    3. Gire el segmento\(AB 90^{\circ}\) en sentido horario alrededor del punto\(B\) Etiquetar cualquier punto nuevo.
    4. Describe una transformación en el segmento\(AB\) que podrías usar para terminar de construir un cuadrado.

    (De la Unidad 1.2.2)

    This page titled 2.2.2: Polígonos similares is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.