2.2.4: Cocientes de Longitud Lateral en Triángulos Similares

Lección

Busquemos longitudes laterales faltantes en triángulos.

Ejercicio\(\PageIndex{1}\): Two-three-four and Four-five-six

\(A\)El triángulo tiene longitudes laterales 2, 3 y 4. \(B\)El triángulo tiene longitudes laterales 4, 5 y 6. ¿Triángulo es\(A\) similar a Triángulo\(B\)?

Ejercicio\(\PageIndex{2}\): Quotients of Sides Within Similar Triangles

Triángulo\(ABC\) es similar a los triángulos\(DEF\),\(GHI\), y\(JKL\). Los factores de escala para las dilataciones que muestran triángulo\(ABC\) es similar a cada triángulo están en la tabla.

Figura\(\PageIndex{1}\)

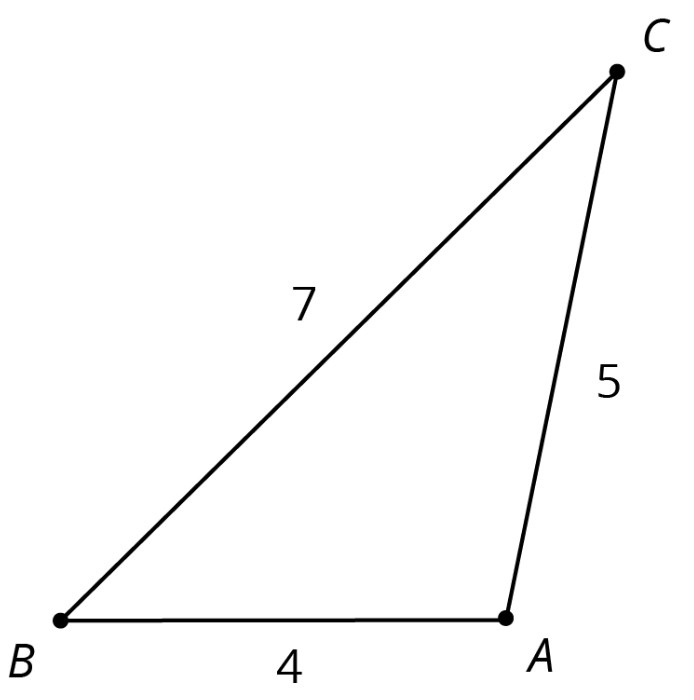
1. Encuentra las longitudes laterales de los triángulos\(DEF\),\(GHI\), y\(JKL\). Gránzalos en la mesa.

Mesa\(\PageIndex{1}\)

triángulo	factor de escala	longitud del lado corto	longitud del lado medio	longitud del lado largo
\(ABC\)	\(1\)	\(4\)	\(5\)	\(7\)
\(DEF\)	\(2\)
\(GHI\)	\(3\)
\(JKL\)	\(\frac{1}{2}\)

2. Tu profesor te asignará una de las tres columnas. Para los cuatro triángulos, encuentra el cociente de las longitudes de los lados del triángulo que se te han asignado y gránzalo en la tabla. ¿Qué notas sobre los cocientes?

Mesa\(\PageIndex{2}\)

triángulo	(lado largo)\(\div\) (lado corto)	(lado largo)\(\div\) (lado medio)	(lado medio)\(\div\) (lado corto)
\(ABC\)	\ (\ div\) (lado corto) ">\(\frac{7}{4}\) o\(1.75\)	\ (\ div\) (lado medio) ">	\ (\ div\) (lado corto) ">
\(DEF\)	\ (\ div\) (lado corto) ">	\ (\ div\) (lado medio) ">	\ (\ div\) (lado corto) ">
\(GHI\)	\ (\ div\) (lado corto) ">	\ (\ div\) (lado medio) ">	\ (\ div\) (lado corto) ">
\(JKL\)	\ (\ div\) (lado corto) ">	\ (\ div\) (lado medio) ">	\ (\ div\) (lado corto) ">

3. Compara tus resultados con los de tu pareja y completa tu tabla.

¿Estás listo para más?

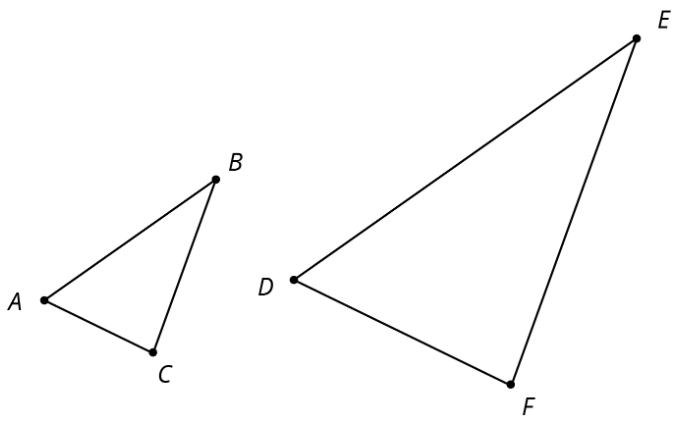
Triángulo\(ABC\) y\(DEF\) son similares. Explique por qué\(\frac{AB}{BC}=\frac{DE}{EF}\).

Figura\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\): Using Side Quotients to Find Side Lengths of Similar Triangles

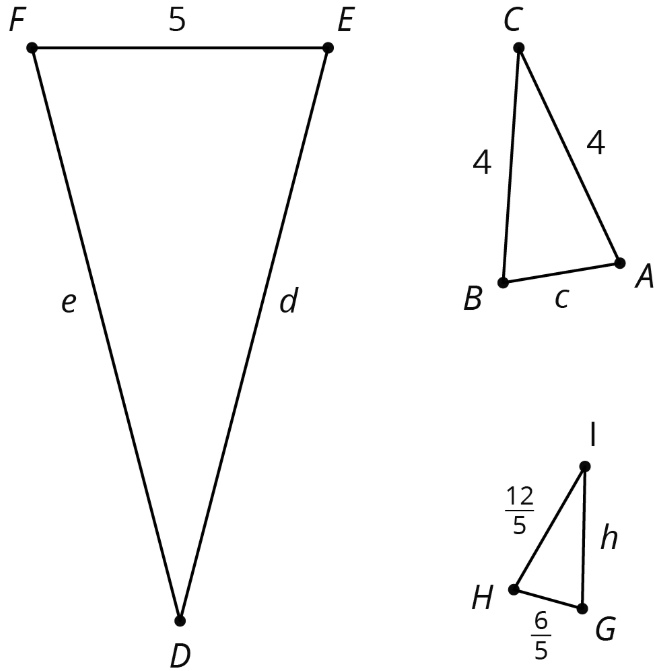
Triángulos\(ABC\),\(EFD\), y\(GHI\) son todos similares. Las longitudes laterales de los triángulos tienen todas las mismas unidades. Encuentra las longitudes de lado desconocidas.

Figura\(\PageIndex{3}\): Tres triángulos. Vértices mayúscula A, B C. Lados B C y A, C longitud 4. Lado A, B longitud minúscula c. Vértices mayúscula I H G. Lado I G longitud minúscula h. Lado I H fracción de longitud 12 sobre 5. Lado H G fracción de longitud 6 sobre 5. Vértices mayúscula D E F. Lado E F 5, Lado F D longitud e minúscula, lado E D longitud minúscula d.

Resumen

Si dos polígonos son similares, entonces las longitudes laterales en un polígono se multiplican por el mismo factor de escala para dar las longitudes laterales correspondientes en el otro polígono.

Para estos triángulos el factor de escala es 2:

Figura\(\PageIndex{4}\)

Aquí hay una tabla que muestra las relaciones entre los lados de longitud corta y media del triángulo pequeño y grande.

Mesa\(\PageIndex{3}\)

	triángulo pequeño	triángulo grande
lado medio	\(4\)	\(8\)
lado corto	\(3\)	\(6\)
(lado medio)\(\div\) (lado corto)	\(\frac{4}{3}\)	\(\frac{8}{6}=\frac{4}{3}\)

Las longitudes del lado medio y el lado corto están en una proporción de\(4\):\(3\). Esto significa que el lado medio en cada triángulo es\(\frac{4}{3}\) tan largo como el lado corto. Esto es cierto para todos los polígonos similares; la relación entre dos lados en un polígono es la misma que la relación de los lados correspondientes en un polígono similar.

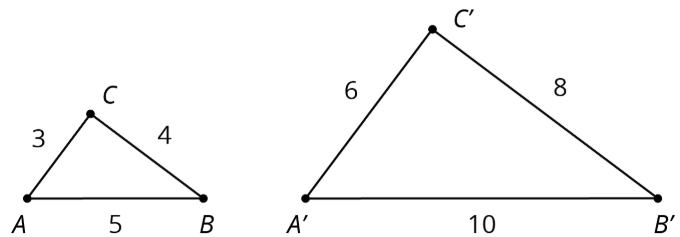
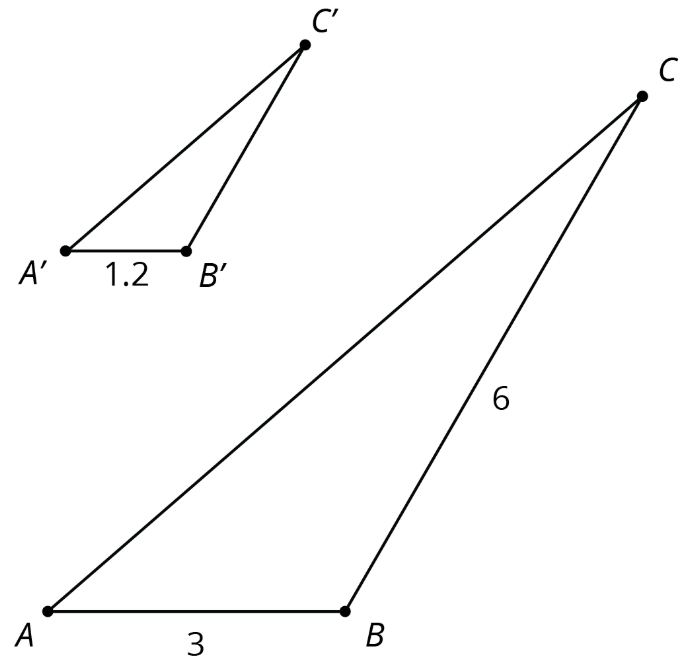
Podemos usar estos datos para calcular longitudes faltantes en polígonos similares. Por ejemplo, los triángulos\(A'B'C'\) y aquí\(ABC\) se muestran son similares. Encontremos la longitud del segmento\(B'C'\).

En triángulo\(ABC\), lado\(BC\) es el doble de largo que lado\(AB\), por lo que esto debe ser cierto para cualquier triángulo que sea similar al triángulo\(ABC\). Ya que\(A'B'\) tiene 1.2 unidades de largo y\(2\cdot 1.2 =2.4\), la longitud del lado\(B'C'\) es de 2.4 unidades.

Figura\(\PageIndex{5}\)

Entradas en el glosario

Definición: Similar

Dos figuras son similares si una puede encajar exactamente sobre la otra después de transformaciones rígidas y dilataciones.

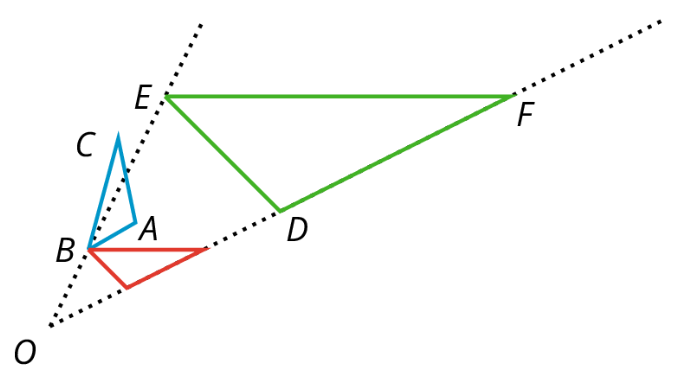
En esta figura, el triángulo\(ABC\) es similar al triángulo\(DEF\).

Si\(ABC\) se gira alrededor del punto\(B\) y luego se dilata con el punto central\(O\), entonces se ajustará exactamente sobre\(DEF\). Esto quiere decir que son similares.

Figura\(\PageIndex{6}\)

Practica

Ejercicio\(\PageIndex{4}\)

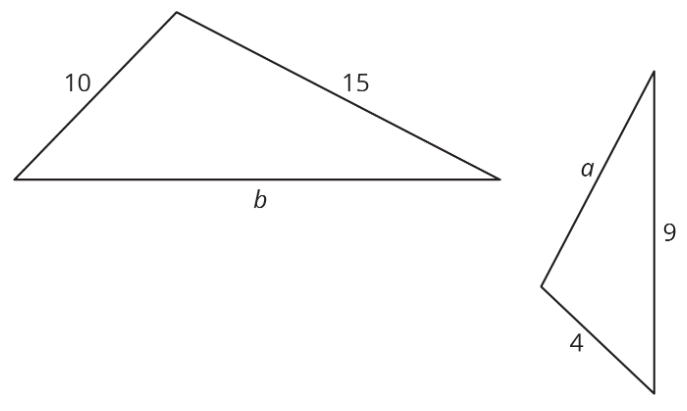
Estos dos triángulos son similares. ¿Qué son\(a\) y\(b\)? Nota: las dos figuras no están dibujadas a escala.

Figura\(\PageIndex{7}\)

Ejercicio\(\PageIndex{5}\)

Aquí está el triángulo\(ABC\). \(XYZ\)El triángulo es similar a\(ABC\) con factor de escala\(\frac{1}{4}\).

Figura\(\PageIndex{8}\)

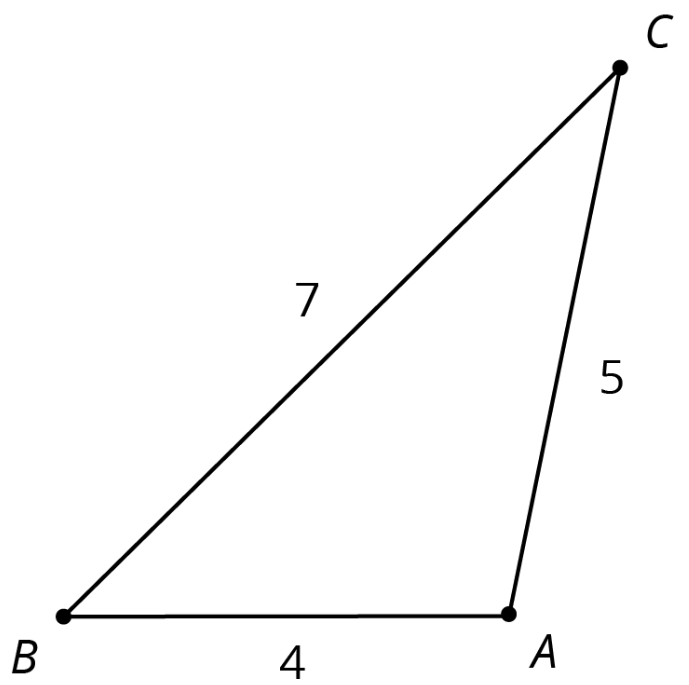
1. Dibuja cómo se\(XYZ\) vería el triángulo.
2. ¿Cómo se\(XYZ\) comparan las medidas de ángulo del triángulo con el triángulo\(ABC\)? Explique cómo sabe.
3. ¿Cuáles son las longitudes laterales del triángulo\(XYZ\)?
4. Para triángulo\(XYZ\), calcule (lado largo)\(\div\) (lado medio) y compare con triángulo\(ABC\).

Ejercicio\(\PageIndex{6}\)

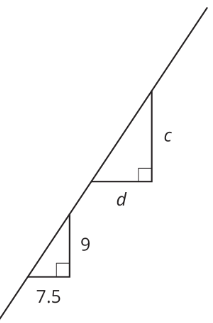
Los dos triángulos mostrados son similares. Encuentra el valor de\(\frac{d}{c}\).

Figura\(\PageIndex{9}\)

Ejercicio\(\PageIndex{7}\)

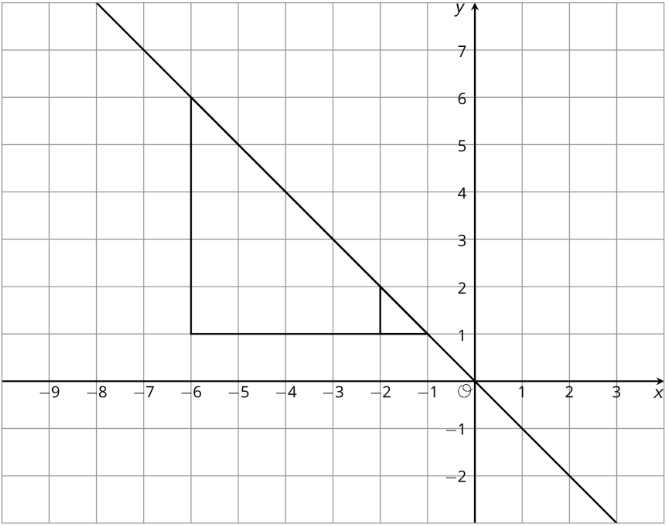
El diagrama muestra dos triángulos anidados que comparten un vértice. Encuentra un centro y un factor de escala para una dilatación que movería el triángulo más grande al triángulo más pequeño.

Figura\(\PageIndex{10}\): Plano coordenado, x, negativo 9 a 3, y, negativo 2 a 7. Una línea a través del negativo 6 coma 6 y el origen. Un triángulo que conecta negativo 6 coma 6, a negativo 6 coma 1, a negativo 1 coma 1. Otro triángulo que conecta negativo 2 coma 2, a negativo 2 coma 1, a negativo 1 coma 1.

(Desde la Unidad 2.1.5)