2.2.3: Triángulos similares

Lección

Veamos triángulos similares.

Ejercicio\(\PageIndex{1}\): Equivalent Expressions

Crea tres expresiones diferentes que sean cada una igual a 20. Cada expresión debe incluir sólo estos tres números: 4, -2 y 10.

Ejercicio\(\PageIndex{2}\): Making Pasta Angles and Triangles

Tu profesor te dará un poco de pasta seca y un conjunto de ángulos.

1. Crea un triángulo usando tres trozos de pasta y ángulo\(A\). Tu triángulo debe incluir el ángulo que te dieron, pero por lo demás eres libre de hacer cualquier triángulo que te guste. Pegue su triángulo de pasta a una hoja de papel para que no se mueva.
   1. Después de haber creado su triángulo, mida la longitud de cada lado con una regla y registre la longitud en el papel al lado. Luego mida los ángulos a los 5 grados más cercanos usando un trasportador y registre estas medidas en su papel.
   2. Encuentra otros dos en la habitación que tengan el mismo ángulo\(A\) y compara tus triángulos. ¿Qué es lo mismo? ¿Qué es diferente? ¿Los triángulos son congruentes? ¿Similares?
   3. ¿Cómo decidiste si eran o no congruentes o similares?
2. Ahora usa más pasta y ángulos\(A\),\(B\), y\(C\) para crear otro triángulo. Pegue este triángulo de pasta en una hoja de papel separada.
   1. Después de haber creado su triángulo, mida la longitud de cada lado con una regla y registre la longitud en el papel al lado. Luego mida los ángulos a los 5 grados más cercanos usando un trasportador y registre estas medidas en su papel.
   2. Encuentra otros dos en la habitación que usaron tus mismos ángulos y compara tus triángulos. ¿Qué es lo mismo? ¿Qué es diferente? ¿Los triángulos son congruentes? ¿Similares?
   3. ¿Cómo decidiste si eran o no congruentes o similares?
3. Aquí está el triángulo\(PQR\). Rompe un nuevo trozo de pasta, diferente en longitud al segmento\(PQ\).

Figura\(\PageIndex{1}\)

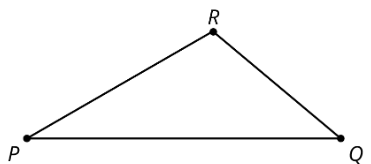
• Cinta adhesiva el trozo de pasta para que quede en la parte superior de la línea\(PQ\) con un extremo de la pasta en\(P\) (si no cabe en la página, rómpelo más). Etiquete el otro extremo del trozo de pasta\(S\).
• Cinta adhesiva un trozo completo de pasta, con un extremo en\(S\), haciendo un ángulo congruente a\(\angle PQR\).
• Pegue un trozo completo de pasta en la parte superior de la línea\(PR\) con un extremo de la pasta en\(P\). Llama al punto donde se encuentran los dos trozos completos de pasta\(T\).
  1. ¿Tu nuevo triángulo de pasta es\(PST\) similar a\(\Delta PQR\)? Explica tu razonamiento.
  2. Si tu trozo de pasta roto tuviera una longitud diferente, ¿seguiría siendo similar el triángulo de la pasta\(\Delta PQR\)? Explica tu razonamiento.

¿Estás listo para más?

Cuadriláteros\(ABCD\) y\(EFGH\) tienen cuatro ángulos que miden\(240^{\circ}\),\(40^{\circ}\),\(40^{\circ}\), y\(40^{\circ}\). ¿Y tiene que ser similar?

Ejercicio\(\PageIndex{3}\): Similar Figures in a Regular Pentagon

1. Este diagrama tiene varios triángulos que son similares al triángulo\(DJI\).

Figura\(\PageIndex{2}\)

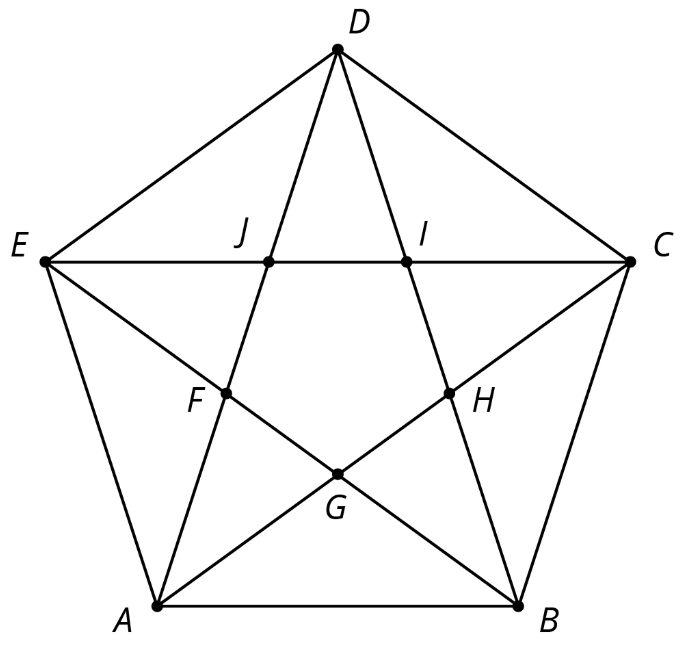
1. Se utilizaron tres factores de escala diferentes para hacer triángulos similares a\(DJI\). En el diagrama, encuentra al menos un triángulo de cada tamaño que sea similar a\(DJI\).
2. Explica cómo sabes que cada uno de estos tres triángulos es similar a\(DJI\).

2. Encuentra un triángulo en el diagrama que no sea similar a\(DJI\).

¿Estás listo para más?

Descubre cómo dibujar algunas líneas más en el diagrama del pentágono para hacer más triángulos similares a\(DJI\).

Resumen

Anteriormente aprendimos que dos polígonos son similares cuando hay una secuencia de traducciones, rotaciones, reflexiones y dilataciones que llevan un polígono al otro. Cuando los polígonos son triángulos, solo necesitamos verificar que ambos triángulos tengan dos ángulos correspondientes para mostrar que son similares, ¿puedes decir por qué?

Aquí hay un ejemplo. El triángulo\(ABC\) y el triángulo tienen\(DEF\) cada uno un ángulo de 30 grados y un ángulo de 45 grados.

Figura\(\PageIndex{3}\)

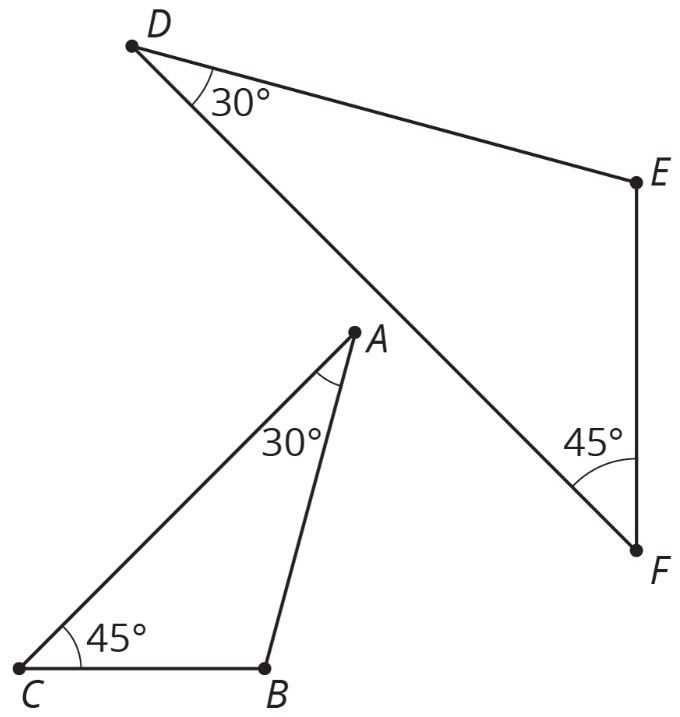
Podemos traducir\(D\) y luego rotar\(A\) para que los dos ángulos de 30 grados estén alineados, dando esta imagen:

Figura\(\PageIndex{4}\)

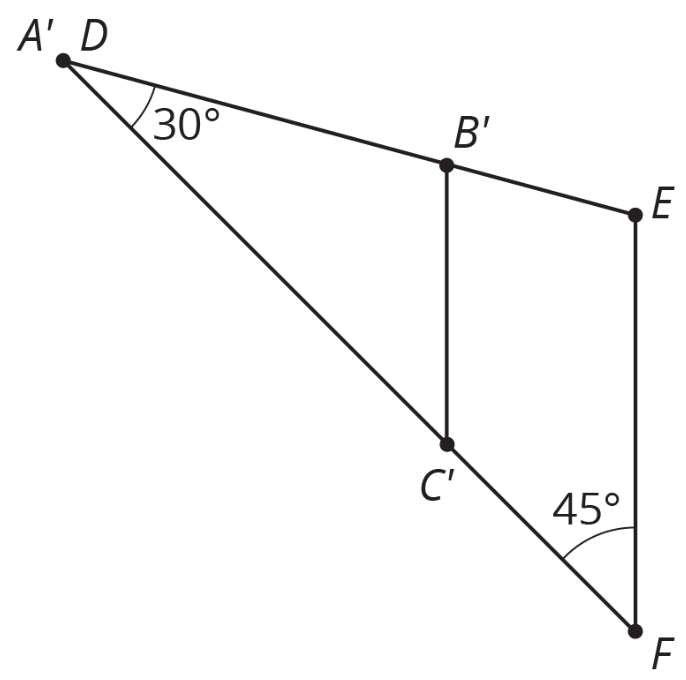
Ahora se\(C'\) moverá a una dilatación con centro\(D\) y factor de escala apropiado\(F\). Esta dilatación también se mueve\(B'\) hacia\(E\), mostrando que los triángulos\(ABC\) y\(DEF\) son similares.

Entradas en el glosario

Definición: Similar

Dos figuras son similares si una puede encajar exactamente sobre la otra después de transformaciones rígidas y dilataciones.

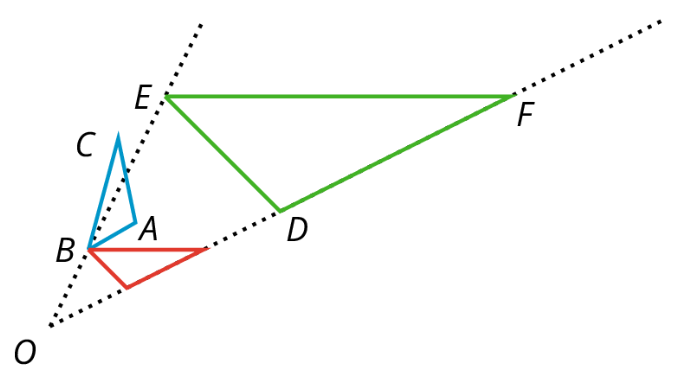
En esta figura, el triángulo\(ABC\) es similar al triángulo\(DEF\).

Si\(ABC\) se gira alrededor del punto\(B\) y luego se dilata con el punto central\(O\), entonces se ajustará exactamente sobre\(DEF\). Esto quiere decir que son similares.

Figura\(\PageIndex{5}\)

Practica

Ejercicio\(\PageIndex{4}\)

En cada par, se dan algunos de los ángulos de dos triángulos en grados. Usa la información para decidir si los triángulos son similares o no. Explique cómo sabe.

• Triángulo A: 53, 71, ___; Triángulo B: 53, 71, ___
• Triángulo C: 90, 37, ___; Triángulo D: 90, 53, ___
• Triángulo E: 63, 45, ___; Triángulo F: 14, 71, ___
• Triángulo G: 121, ___, ___; Triángulo H: 70, ___, ___

Ejercicio\(\PageIndex{5}\)

1. Dibuja dos triángulos equiláteros que no sean congruentes.
2. Mide las longitudes laterales y los ángulos de tus triángulos. ¿Los dos triángulos son similares?
3. ¿Crees que dos triángulos equiláteros serán similares siempre, a veces o nunca? Explica tu razonamiento.

Ejercicio\(\PageIndex{6}\)

En la figura, la línea\(BC\) es paralela a la línea\(DE\).

Figura\(\PageIndex{6}\)

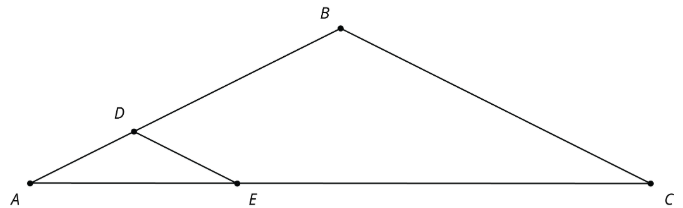
Explique por qué\(\Delta ABC\) es similar a\(\Delta ADE\).

Ejercicio\(\PageIndex{7}\)

El cuadrilátero\(PQRS\) en el diagrama es un paralelogramo. Dejar\(P'Q'R'S'\) ser la imagen de\(PQRS\) después de aplicar una dilatación centrada en un punto O (no mostrado) con factor de escala 3.

Figura\(\PageIndex{7}\)

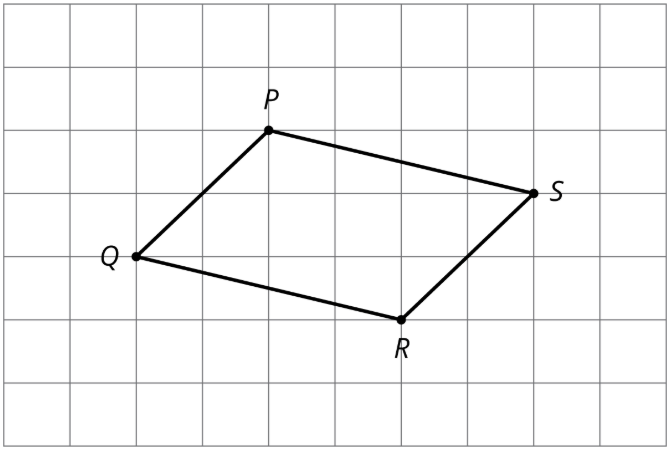
¿Cuál de las siguientes cosas es cierto?

1. \(P'Q'=PQ\)
2. \(P'Q'=3PQ\)
3. \(PQ=3P'Q'\)
4. No se puede determinar a partir de la información proporcionada

(De la Unidad 2.1.4)

Ejercicio\(\PageIndex{8}\)

Describir una secuencia de transformaciones para las cuales Cuadrilátero P es la imagen de Cuadrilátero Q.

Figura\(\PageIndex{8}\): Dos cuadriláteros en un plano x y. Origen 0. Eje vertical de negativo 5 a 6 por 1s. Eje horizontal de negativo 2 a 12 por 1s. El cuadrilátero, etiquetado P, tiene puntos en 3 coma 3, 6 coma 6, 4 coma 1 y 4 coma 4. Cuadrilátero, etiquetado Q, tiene puntos en 7 coma negativa 4, 12 coma negativa 6, 10 coma negativa 3, 10 coma negativa 4.

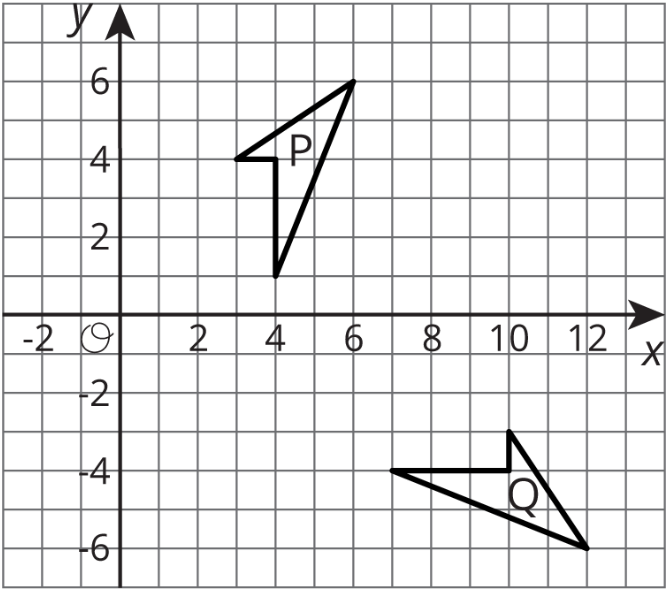
(De la Unidad 1.1.6)