2.3.3: Uso de ecuaciones para líneas
- Page ID
- 118666
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Escribamos ecuaciones para líneas.
Ejercicio\(\PageIndex{1}\): Missing center
Una dilatación con factor de escala 2 envía\(A\) a\(B\). ¿Dónde está el centro de la dilatación?
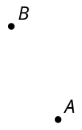
Ejercicio\(\PageIndex{2}\): Writing Relationships from Two Points
Aquí hay una línea.
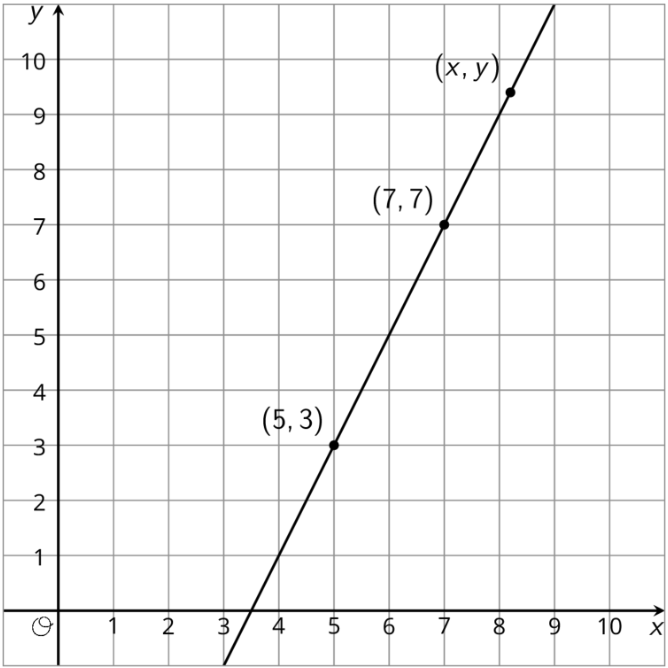
- Usando lo que sabes sobre triángulos similares, encuentra una ecuación para la línea en el diagrama.
- ¿Cuál es la pendiente de esta línea? ¿Aparece en tu ecuación?
- ¿\((9,11)\)También está en la línea? ¿Cómo lo sabes?
- ¿\((100,93)\)También está en la línea?
¿Estás listo para más?
Hay muchas maneras diferentes de escribir una ecuación para una línea como la del problema. ¿\(\frac{y-3}{x-6}=2\)Representa la línea? ¿Y qué pasa\(\frac{y-6}{x-4}=5\)? ¿Y qué pasa\(\frac{y+5}{x-1}=2\)? Explica tu razonamiento.
Ejercicio\(\PageIndex{3}\): Dilations and Slope Triangles
Aquí está el triángulo\(ABC\).
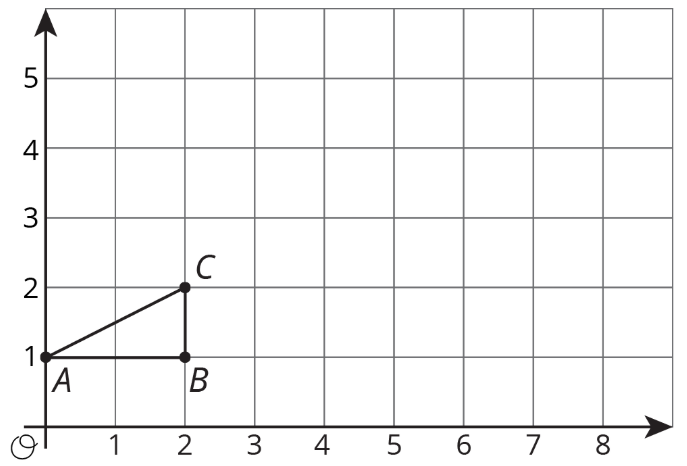
- Dibuja la dilatación del triángulo\(ABC\) con centro\((0,1)\) y factor de escala 2.
- Dibuja la dilatación del triángulo\(ABC\) con centro\((0,1)\) y factor de escala 2.5.
- ¿Dónde se\(C\) mapea por la dilatación con centro\((0,1)\) y factor de escala?
- ¿Para qué factor de escala\((0,1)\) envía\(C\) la dilatación con centro\((9,5.5)\)? Explique cómo sabe.
Resumen
Podemos usar lo que sabemos de pendiente para decidir si un punto se encuentra en una línea. Aquí hay una línea con algunos puntos etiquetados.
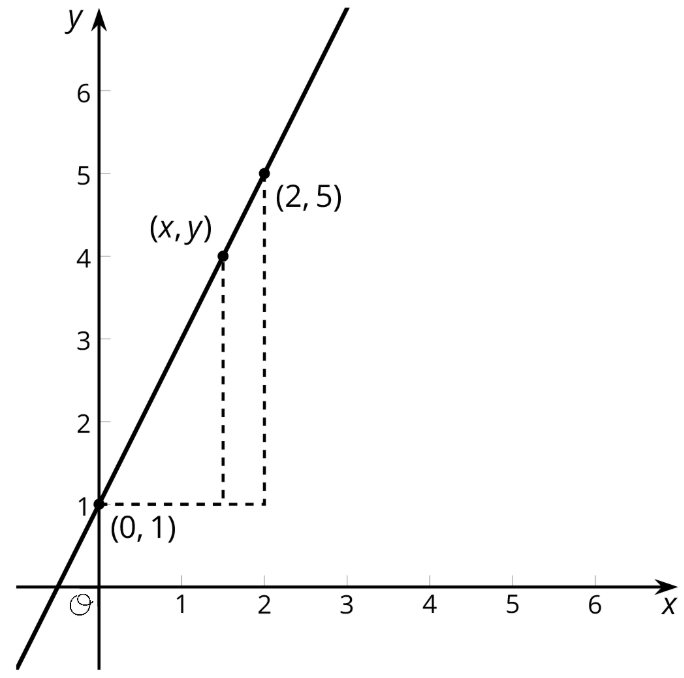
El triángulo de pendiente con vértices\((0,1)\) y\((2,5)\) da una pendiente de\(\frac{5-1}{2-0}=2\). El triángulo de pendiente con vértices\((0,1)\) y\((x,y)\) da una pendiente de\(\frac{y-1}{x}\). Dado que estas pendientes son las mismas,\(\frac{y-1}{x}=2\) es una ecuación para la línea. Entonces, si queremos comprobar si el punto\((11,23)\) está o no en esta línea, podemos comprobarlo\(\frac{23-1}{11}=2\). Ya que\((11,23)\) es una solución a la ecuación, ¡está en la línea!
Entradas en el glosario
Definición: Similar
Dos figuras son similares si una puede encajar exactamente sobre la otra después de transformaciones rígidas y dilataciones.
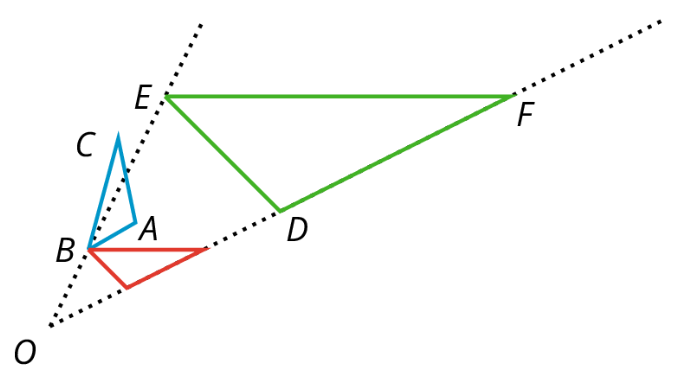
En esta figura, el triángulo\(ABC\) es similar al triángulo\(DEF\).
Si\(ABC\) se gira alrededor del punto\(B\) y luego se dilata con el punto central\(O\), entonces se ajustará exactamente sobre\(DEF\). Esto quiere decir que son similares.
Definición: Slope
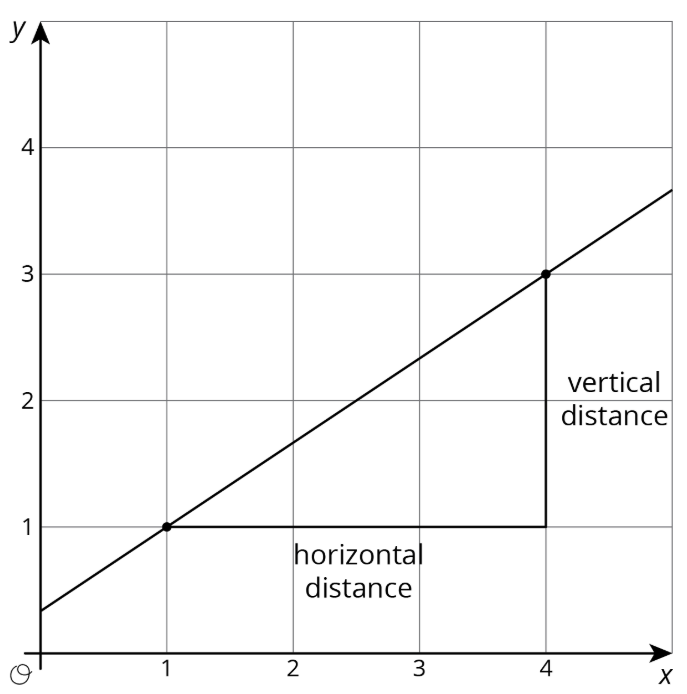
La pendiente de una línea es un número que podemos calcular usando dos puntos cualesquiera en la línea. Para encontrar la pendiente, divida la distancia vertical entre los puntos por la distancia horizontal.
La pendiente de esta línea es de 2 dividido por 3 o\(\frac{2}{3}\).
Practica
Ejercicio\(\PageIndex{4}\)
Seleccione todos los puntos que están en la línea a través\((0,5)\) y\((2,8)\).
- \((4,11)\)
- \((5,10)\)
- \((6,14)\)
- \((30,50)\)
- \((40,60)\)
Ejercicio\(\PageIndex{5}\)
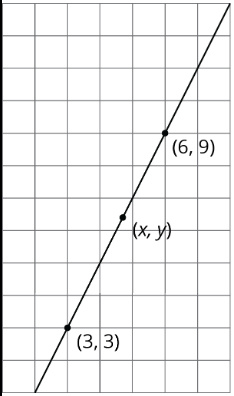
Los tres puntos mostrados están en la línea. Encuentra una ecuación que relacione\(x\) y\(y\).
Ejercicio\(\PageIndex{6}\)
Aquí está el triángulo\(ABC\).
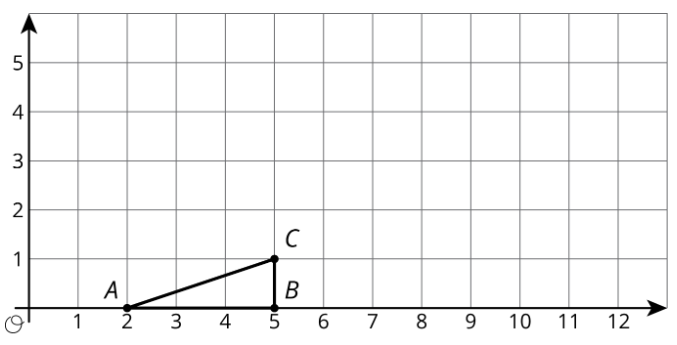
- Dibuja la dilatación del triángulo\(ABC\) con centro\((2,0)\) y factor de escala 2.
- Dibuja la dilatación del triángulo\(ABC\) con centro\((2,0)\) y factor de escala 3.
- Dibuja la dilatación del triángulo\(ABC\) con centro\((2,0)\) y factor de escala\(\frac{1}{2}\).
- ¿Cuáles son las coordenadas de la imagen de punto\(C\) cuando el triángulo\(ABC\) se dilata con centro\((2,0)\) y factor de escala\(s\)?
- Escribe una ecuación para la línea que contenga todas las imágenes posibles de punto\(C\).
Ejercicio\(\PageIndex{7}\)
Aquí hay algunos segmentos de línea.
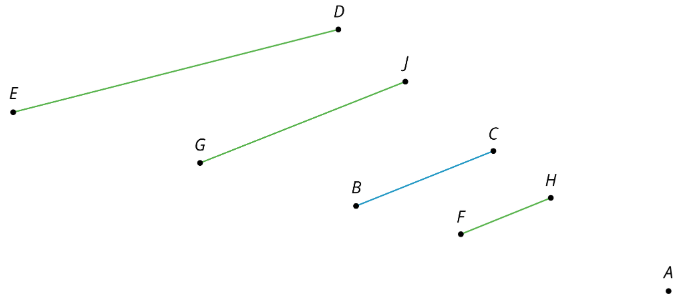
- ¿Qué segmento es una dilatación de\(\overline{BC}\) usar\(A\) como centro de dilatación y factor de escala de\(\frac{2}{3}\)?
- ¿Qué segmento es una dilatación de\(\overline{BC}\) usar\(A\) como centro de dilatación y factor de escala de\(\frac{3}{2}\)?
- ¿Qué segmento no es una dilatación de\(\overline{BC}\), y cómo lo sabes?
(De la Unidad 2.1.4)