2.3.2: Escribir ecuaciones para líneas
- Page ID
- 118667
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Exploremos la relación entre los puntos de una línea y la pendiente de la línea.
Ejercicio\(\PageIndex{1}\): Coordinates and Lengths in the Coordinate Plane
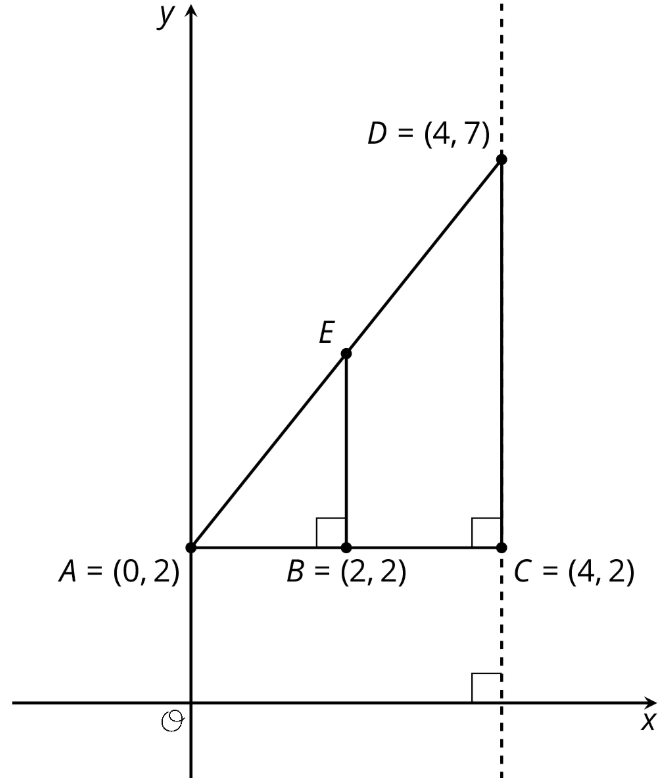
Encuentra cada uno de los siguientes y explica tu razonamiento:
- La longitud del segmento\(BE\).
- Las coordenadas de\(E\).
Ejercicio\(\PageIndex{2}\): What We Mean by an Equation of a Line
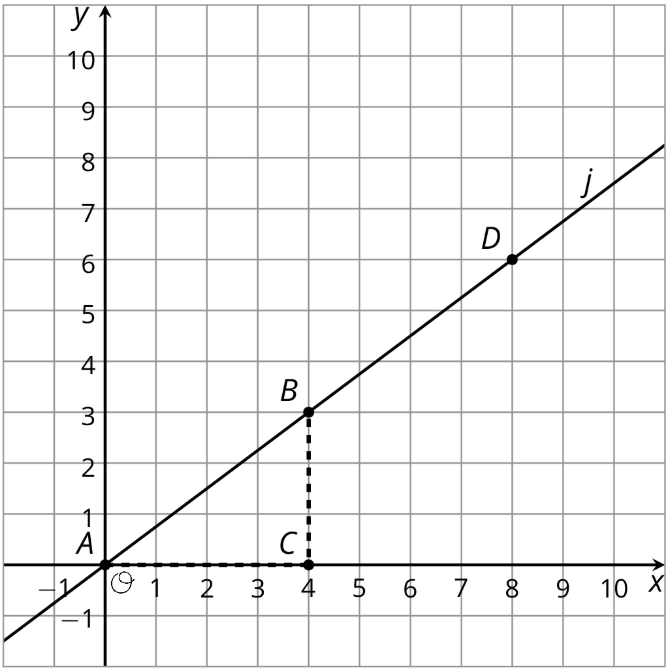
\(j\)La línea se muestra en el plano de coordenadas.
- ¿Cuáles son las coordenadas de\(B\) y\(D\)?
- ¿El punto\((20, 15)\) en línea\(j\)? Explica cómo sabes.
- ¿El punto\((100, 75)\) en línea\(j\)? Explica cómo sabes.
- ¿El punto\((90, 68)\) en línea\(j\)? Explica cómo sabes.
- Supongamos que conoce las\(y\) coordenadas\(x\) - y -de un punto. Escribe una regla que te permita probar si el punto está en línea\(j\).
Ejercicio\(\PageIndex{3}\): Writing Relationships from Slope Triangles
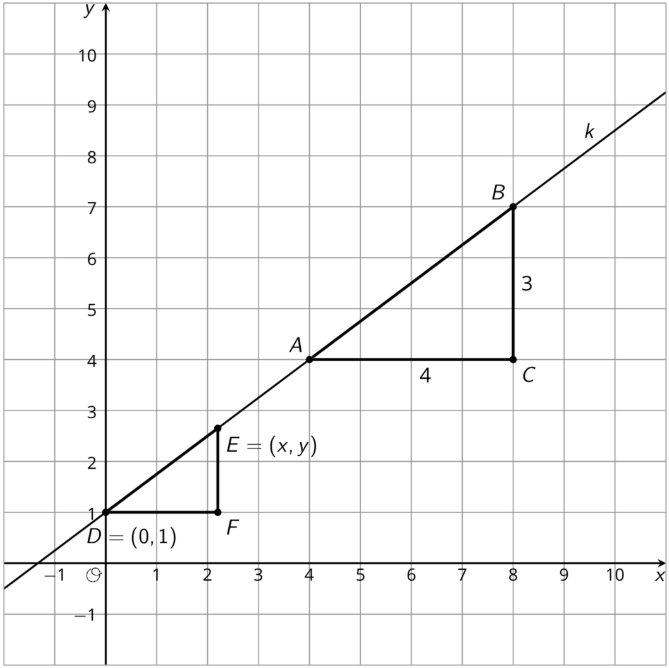
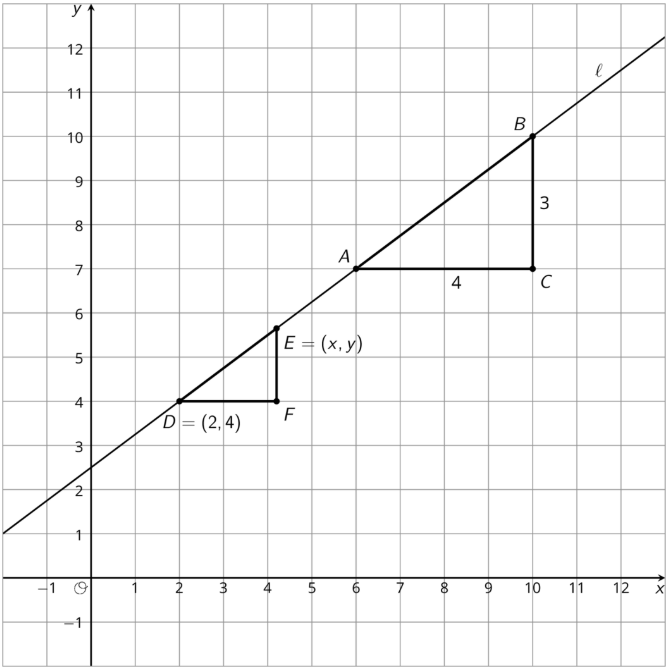
Aquí hay dos diagramas:
- Complete cada diagrama para que todos los segmentos verticales y horizontales tengan expresiones para sus longitudes.
- Usa lo que sabes sobre triángulos similares para encontrar una ecuación para el cociente de las longitudes laterales verticales y horizontales de\(\Delta DFE\) en cada diagrama.
¿Estás listo para más?
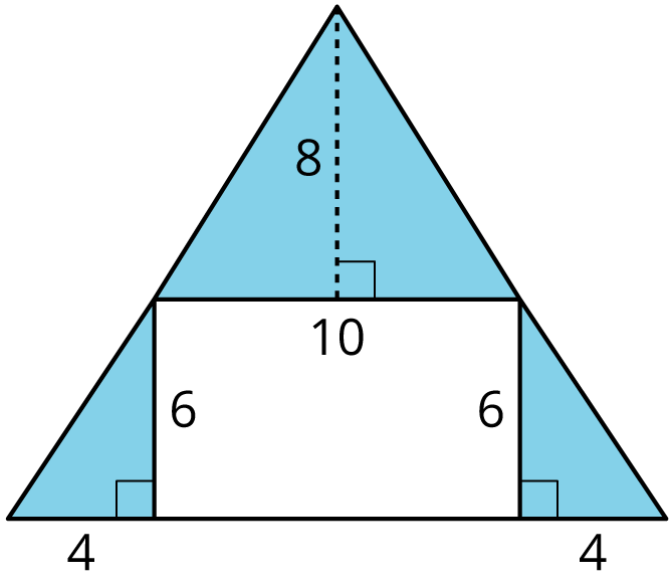
- Encuentra el área de la región sombreada sumando las áreas de los triángulos sombreados.
- Encuentra el área de la región sombreada restando el área de la región no sombreada del triángulo grande.
- ¿Qué está pasando aquí?
Resumen
Aquí están los puntos\(A\),\(C\), y\(E\) en la misma línea. Triángulos\(ABC\) y\(ADE\) son triángulos de pendiente para la línea así que sabemos que son triángulos similares. Usemos su similitud para entender mejor la relación entre\(x\) y\(y\), que conforman las coordenadas de punto\(E\).
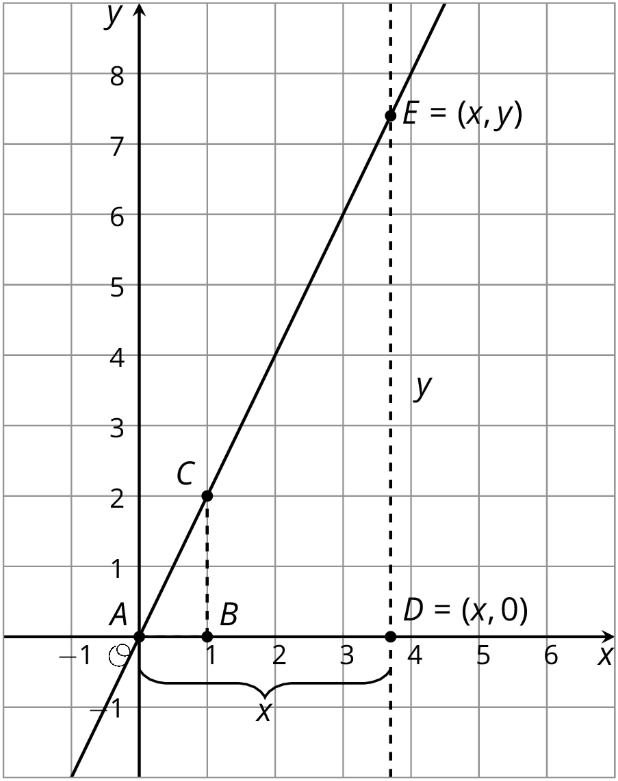
La pendiente para triángulo\(ABC\) es\(\frac{2}{1}\) ya que el lado vertical tiene longitud 2 y el lado horizontal tiene longitud 1. La pendiente que encontramos para triángulo\(ADE\) es\(\frac{y}{x}\) porque el lado vertical tiene longitud\(y\) y el lado horizontal tiene longitud\(x\). Estas dos pendientes deben ser iguales ya que son de triángulos de pendiente para una misma línea, y así:\(\frac{2}{1}=\frac{y}{x}\).
Ya que\(\frac{2}{1}=2\) esto significa que el valor de\(y\) es el doble del valor de\(x\), o eso\(y=2x\). ¡Esta ecuación es cierta para cualquier punto\((x,y)\) de la línea!
Aquí hay dos triángulos de pendiente diferentes. Podemos utilizar el mismo razonamiento para describir la relación entre\(x\) y\(y\) para este punto\(E\).
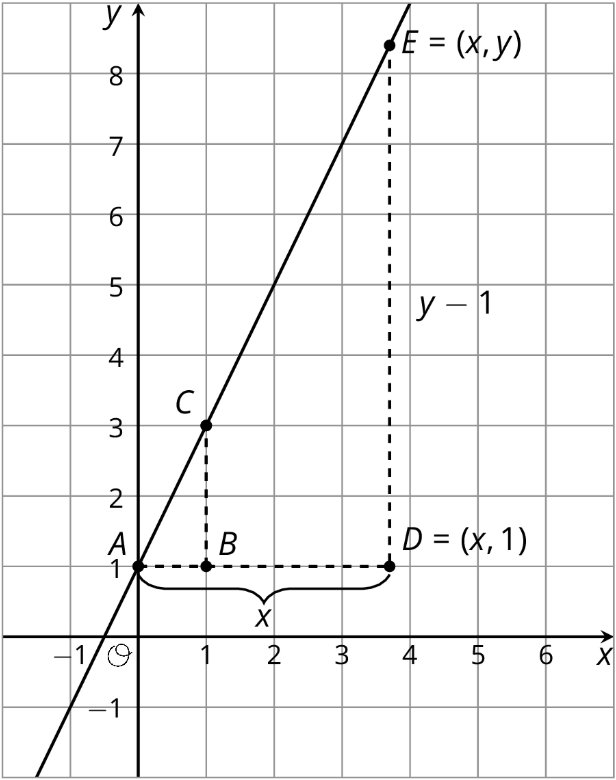
La pendiente para triángulo\(ABC\) es\(\frac{2}{1}\) ya que el lado vertical tiene longitud 2 y el lado horizontal tiene longitud 1. Para triángulo\(ADE\), el lado horizontal tiene longitud\(x\). El lado vertical tiene longitud\(y-1\) porque la distancia desde\((x,y)\) el\(x\) eje -es\(y\) pero el lado vertical del triángulo se detiene a 1 unidad menos del\(x\) eje -eje. Entonces la pendiente que encontramos para triángulo\(ADE\) es\(\frac{y-1}{x}\). Las pendientes para los dos triángulos de pendiente son iguales, es decir:\(\frac{2}{1}=\frac{y-1}{x}\)
Ya que\(y-1\) es dos veces\(x\), otra forma de escribir esta ecuación es\(y-1=2x\). ¡Esta ecuación es cierta para cualquier punto\((x,y)\) de la línea!
Entradas en el glosario
Definición: Similar
Dos figuras son similares si una puede encajar exactamente sobre la otra después de transformaciones rígidas y dilataciones.
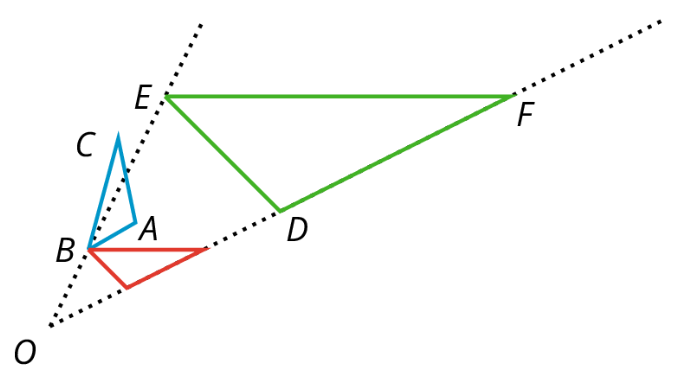
En esta figura, el triángulo\(ABC\) es similar al triángulo\(DEF\).
Si\(ABC\) se gira alrededor del punto\(B\) y luego se dilata con el punto central\(O\), entonces se ajustará exactamente sobre\(DEF\). Esto quiere decir que son similares.
Definición: Pendiente
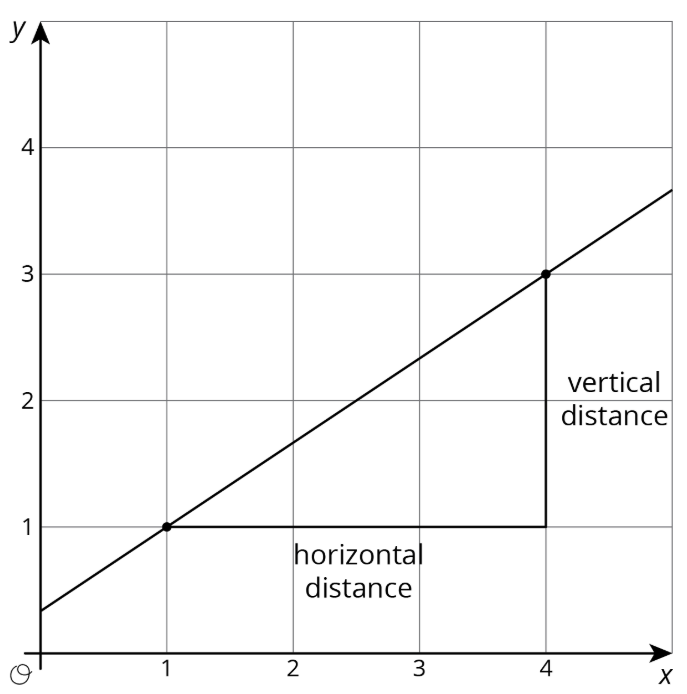
La pendiente de una línea es un número que podemos calcular usando dos puntos cualesquiera en la línea. Para encontrar la pendiente, divida la distancia vertical entre los puntos por la distancia horizontal.
La pendiente de esta línea es de 2 dividido por 3 o\(\frac{2}{3}\).
Practica
Ejercicio\(\PageIndex{4}\)
Por cada par de puntos, encuentra la pendiente de la línea que pasa por ambos puntos. Si te quedas atascado, intenta trazar los puntos en papel cuadriculado y dibujando la línea a través de ellos con una regla.
- \((1,1)\)y\((7,5)\)
- \((1,1)\)y\((5,7)\)
- \((2,5)\)y\((-1,2)\)
- \((2,5)\)y\((-7,-4)\)
Ejercicio\(\PageIndex{5}\)
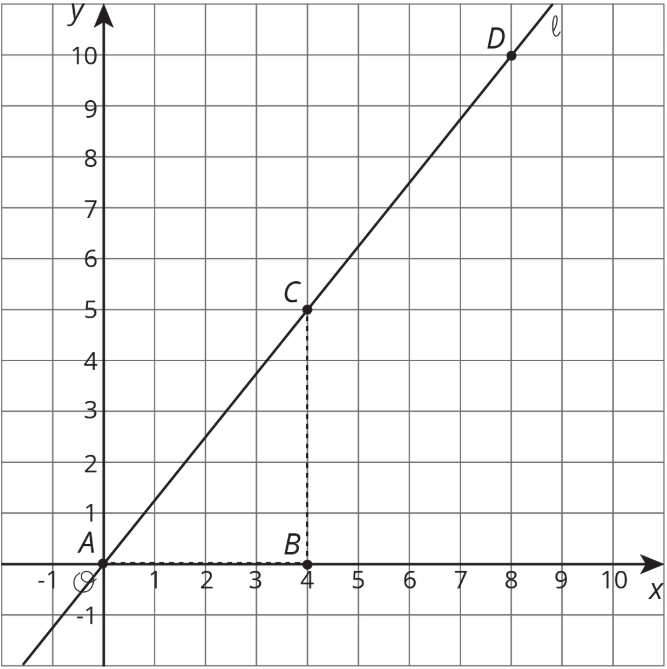
\(l\)La línea se muestra en el plano de coordenadas.
- ¿Cuáles son las coordenadas de los puntos\(B\) y\(D\)?
- ¿El punto está\((16,20)\) en línea\(l\)? Explica cómo sabes.
- ¿El punto está\((20,24)\) en línea\(l\)? Explica cómo sabes.
- ¿El punto está\((80,100)\) en línea\(l\)? Explica cómo sabes.
- Escribe una regla que te permita probar si\((x,y)\) está en línea\(l\).
Ejercicio\(\PageIndex{6}\)
Considera la línea gráfica.
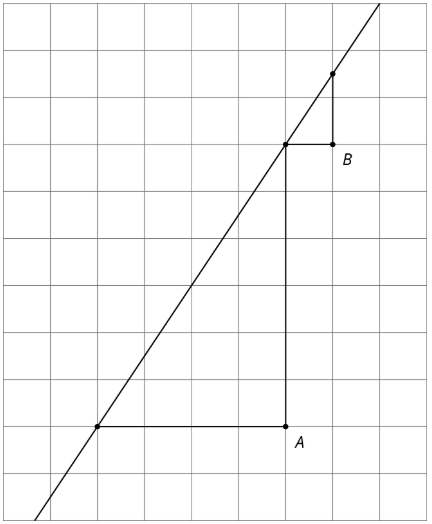
Mai usa el Triángulo A y dice que la pendiente de esta línea es\(\frac{6}{4}\). Elena usa el Triángulo B y dice que no, la pendiente de esta línea es de 1.5. ¿Estás de acuerdo con alguno de ellos? Explique.
Ejercicio\(\PageIndex{7}\)
Un rectángulo tiene longitud 6 y altura 4.
¿Cuál de estos te diría que el cuadrilátero definitivamente no\(ABCD\) es similar a este rectángulo? Seleccione todas las que correspondan.
- \(AB=BC\)
- \(m\angle ABC=105^{\circ}\)
- \(AB=8\)
- \(BC=8\)
- \(BC=2\cdot AB\)
- \(2\cdot AB=3\cdot BC\)
(De la Unidad 2.2.1)