3.1.1: Comprender las relaciones proporcionales

Lección

Estudiemos algunas gráficas.

Ejercicio\(\PageIndex{1}\): Notice and Wonder: Two Graphs

Figura\(\PageIndex{1}\): Dos gráficos. ambas gráficas, eje horizontal, escala 0 a 18, por 2's. eje vertical, escala 0 a 6, por 1's. gráfico sobre eje horizontal izquierdo etiquetado distancia recorrida en centímetros, eje vertical etiquetado tiempo transcurrido en segundos. 2 líneas en gráfico, etiquetadas g y f. la línea g pasa por origen y 6 coma 3. línea f pasa por origen y 8 coma 2. gráfico a la derecha, ejes y líneas no etiquetadas. línea pasa por origen y 3 coma 1.

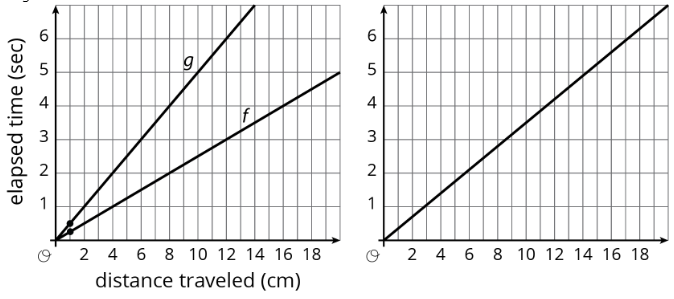
¿Qué notas? ¿Qué te preguntas?

Ejercicio\(\PageIndex{2}\): Moving Through Representations

Una mariquita y una hormiga se mueven a velocidades constantes. Los diagramas con marcas de graduación muestran sus posiciones en diferentes momentos. Cada marca representa 1 centímetro.

Figura\(\PageIndex{2}\): 4 líneas numéricas, 30 marcas de graduación uniformemente espaciadas. primera línea, 0 segundos, Lady Bug y hormiga ambas en la 5ta marca de garrapata, etiquetadas start. segunda línea, 2 segundos, Lady Bug en la 9ª marca de garrapata y hormiga en la marca de 11o. línea thrid, 4 segundos, lady bug en la marca 13 y hormiga en la marca 17a. cuarta línea, 6 segundos, Lady Bug en la marca 17 y hormiga en la marca 23.

Figura\(\PageIndex{3}\): Gráfico. eje horizontal, distancia recorrida en centímetros, 20 unidades. eje vertical, tiempo transcurrido en segundos, 6 unidades. 2 líneas graficadas, etiquetadas u y v. la línea u pasa por origen y 2ª línea a la derecha y 1ª línea hacia arriba. la línea v pasa por origen y 3ª línea a la derecha y 1ª línea hacia arriba.

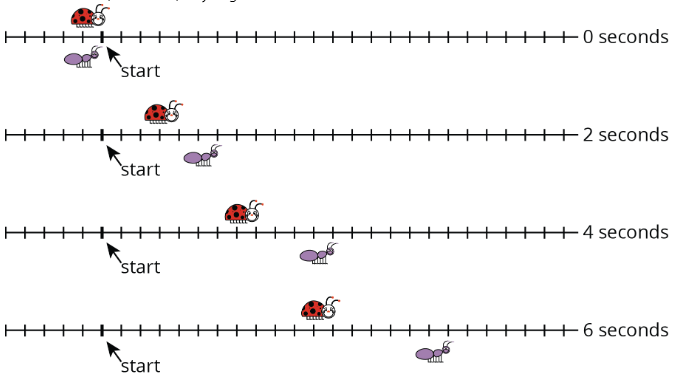
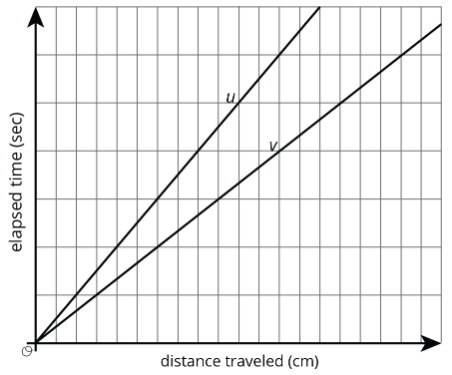
1. Líneas\(u\) y\(v\) también muestran las posiciones de los dos bichos. ¿Qué línea muestra el movimiento de la mariquita? ¿Qué línea muestra el movimiento de la hormiga? Explica tu razonamiento.
2. ¿Cuánto tarda la mariquita en recorrer 12 cm? ¿La hormiga?
3. Escala los ejes vertical y horizontal etiquetando cada línea de rejilla con un número. Deberá usar la información de tiempo y distancia que se muestra en los diagramas de marcas de verificación.
4. Marcar y etiquetar el punto en línea\(u\) y el punto en línea\(v\) que representan el tiempo y la posición de cada error después de viajar 1 cm.

¿Estás listo para más?

1. ¿Qué tan rápido viaja cada bicho?
2. ¿Alguna vez habrá un momento en que la hormiga esté el doble de lejos del inicio que la mariquita? Explica o muestra tu razonamiento.

Ejercicio\(\PageIndex{3}\): Moving Twice as Fast

Consulte los diagramas de marca y grafica en la actividad anterior cuando sea necesario.

1. Imagina un bicho que se mueve el doble de rápido que la mariquita. En cada diagrama de marcas, marque la posición de este error.
2. Trace las posiciones de este error en los ejes de coordenadas con líneas\(u\) y\(v\), y conéctelos con una línea.
3. Escribe una ecuación para cada una de las tres líneas.

Resumen

Graficar es una manera de ayudarnos a dar sentido a las relaciones. Pero la gráfica de una línea en unos ejes de coordenadas sin escala ni etiquetas no es muy útil. Por ejemplo, digamos que sabemos que en paseos en bicicleta más largos, Kiran puede recorrer 4 millas cada 16 minutos y Mai puede recorrer 4 millas cada 12 minutos. Aquí están las gráficas de estas relaciones:

Figura\(\PageIndex{4}\): Gráfico. eje horizontal, 15 unidades. eje vertical, 12 unidades. 2 líneas grapadas. primera línea pasa por origen y 5ta unidad sobre y 4ta unidad arriba. segunda línea pasa por origen y 4ta unidad sobre 3ra unidad hacia arriba.

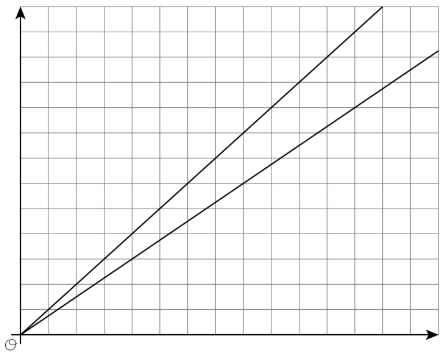
¡Sin etiquetas ni siquiera podemos decir qué línea es Kiran y cuál es Mai! Sin etiquetas y una escala en los ejes, no podemos usar estas gráficas para responder preguntas como:

1. ¿Qué gráfico va con qué jinete?
2. ¿Quién viaja más rápido?
3. Si Kiran y Mai inician un viaje en bicicleta al mismo tiempo, ¿qué tan lejos están después de 24 minutos?
4. ¿Cuánto tardará cada uno de ellos en llegar al final del carril bici de 12 millas?

Aquí están las mismas gráficas, pero ahora con etiquetas y escala:

Figura\(\PageIndex{5}\): Gráfico. eje horizontal, distancia en millas, escala 0 a 14, por 2's. eje vertical, tiempo en minutos, escala 0 a 48, por 8's. primera línea pasa por origen, 1 coma 4, 4 coma 16, y 10 coma 40. segunda línea pasa por origen, 1 coma 3, 4 coma 12 y 10 coma 30.

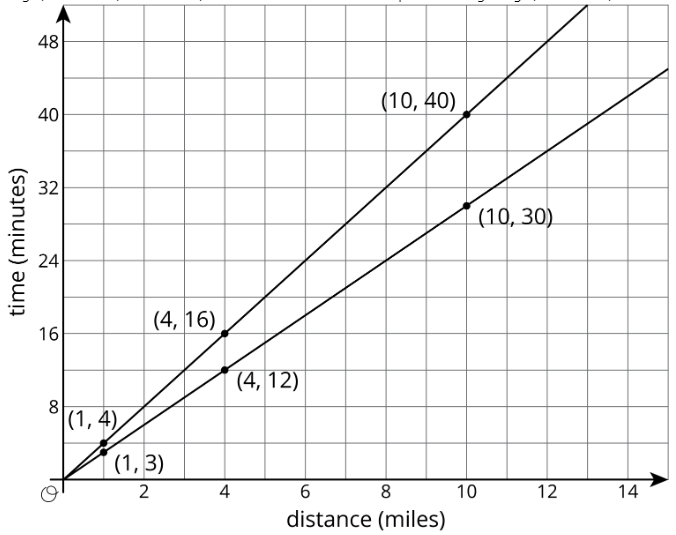
Repasando las preguntas anteriores:

1. ¿Qué gráfico va con cada piloto? Si Kiran cabalga 4 millas en 16 minutos, entonces el punto está en su gráfica. Si viaja por 1 milla, tardará 4 minutos. 10 millas tardarán 40 minutos. Entonces la gráfica superior representa el paseo de Kiran. Los puntos de Mai para las mismas distancias son,, y, entonces el suyo es el gráfico inferior. (Una letra junto a cada línea nos ayudaría a recordar cual es cual!)
2. ¿Quién viaja más rápido? Mai cabalga más rápido porque puede recorrer la misma distancia que Kiran en menos tiempo.
3. Si Kiran y Mai inician un viaje en bicicleta al mismo tiempo, ¿qué tan lejos están después de 20 minutos? Los puntos en las gráficas a la altura 20 son 5 millas para Kiran y un poco menos de 7 millas para Mai.
4. ¿Cuánto tardará cada uno de ellos en llegar al final del carril bici de 12 millas? Los puntos en las gráficas a una distancia horizontal de 12 son 36 minutos para Mai y 48 minutos para Kiran. (¡El tiempo de Kiran después de 12 millas está casi fuera de la red!)

Entradas en el glosario

Definición: Constante de proporcionalidad

En una relación proporcional, los valores de una cantidad se multiplican cada uno por el mismo número para obtener los valores de la otra cantidad. A este número se le llama la constante de proporcionalidad.

En este ejemplo, la constante de proporcionalidad es 3, porque\(2\cdot 3=6\),\(3\cdot 3=9\), y\(5\cdot 3=15\). Esto significa que hay 3 manzanas por cada 1 naranja en la ensalada de frutas.

Mesa\(\PageIndex{1}\)

número de naranjas	número de manzanas
\(2\)	\(6\)
\(3\)	\(9\)
\(5\)	\(15\)

Practica

Ejercicio\(\PageIndex{4}\)

Priya trota a velocidad constante. La relación entre su distancia y tiempo se muestra en la gráfica. Diego bicis a una velocidad constante el doble de rápido que Priya. Dibuje una gráfica que muestre la relación entre la distancia y el tiempo de Diego.

Figura\(\PageIndex{6}\)

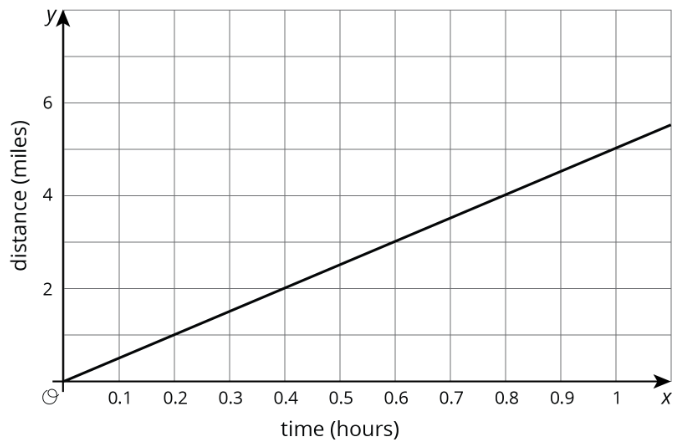
Ejercicio\(\PageIndex{5}\)

Una granja de arándanos que elija ofrece 6 libras de arándanos por $16.50.

Dibuje una gráfica de la relación entre costo y libras de arándanos.

Figura\(\PageIndex{7}\)

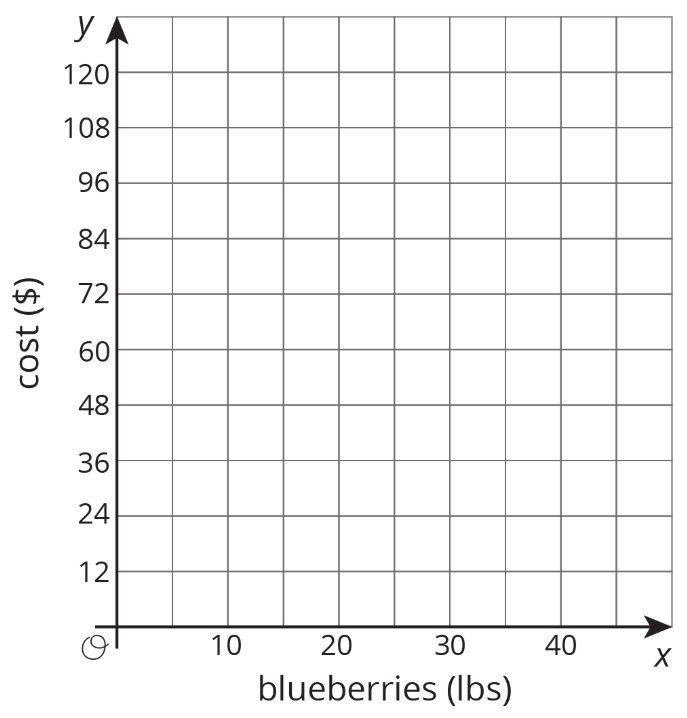
Ejercicio\(\PageIndex{6}\)

Una línea contiene los puntos\((-4,1)\) y\((4,6)\). Decidir si cada uno de estos puntos también está o no en la línea:

1. \((0, 3.5)\)
2. \((12, 11)\)
3. \((80, 50)\)
4. \((-1, 2.875)\)

(De la Unidad 2.3.3)

Ejercicio\(\PageIndex{7}\)

Los puntos\((2,-4)\),\((x,y)\),\(A\), y\(B\) todos se encuentran en la línea. Encuentra una ecuación que relacione\(x\) y\(y\).

Figura\(\PageIndex{8}\): Gráfico. eje horizontal, escala 0 a 11, por 1's. eje vertical, escala -5 a 3, por 1's. línea que pasa por 2 coma -4, x coma y, 6 coma -1, etiquetada A, y 10 coma 2, etiquetada B. triángulos rectos dibujados entre 1er y 2do puntos y puntos A y B. vértice donde está el ángulo de 90 grados, etiquetado F en primer triángulo y C en segundo triángulo. C está en 10 coma -1.

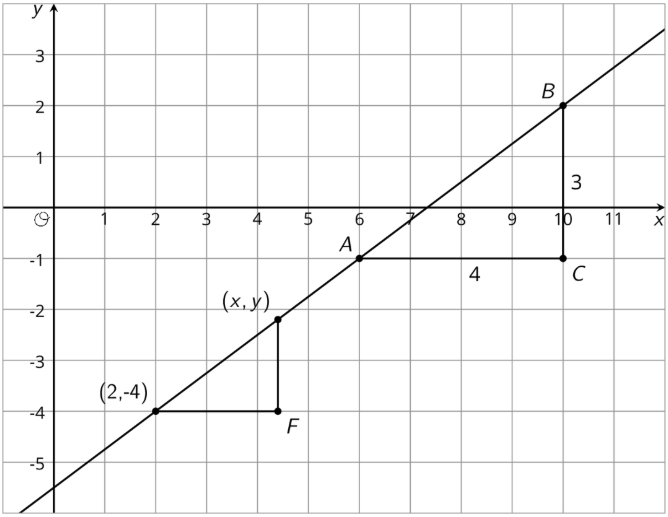
(De la Unidad 2.3.2)