Saltar al contenido principal
LibreTexts Español

3.1.2: Gráficas de Relaciones Proporcionales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118739

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Pensemos en la escala.

    Ejercicio\(\PageIndex{1}\): An Unknown Situation

    Aquí hay una gráfica que podría representar una variedad de situaciones diferentes.

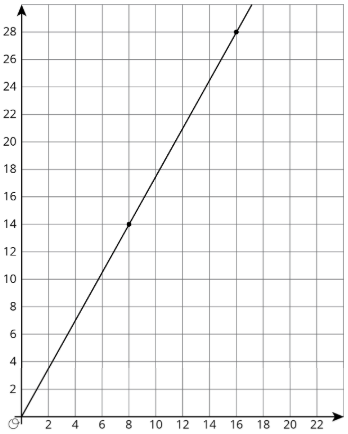
    clipboard_e9639de905a47a3deb21802bfc5cb5bf3.png
    Figura\(\PageIndex{1}\)
    1. Escribe una ecuación para la gráfica.
    2. Esbozar una nueva gráfica de esta relación.
    clipboard_eb2e45db5890b6d9beaacd75bf84b060e.png
    Figura\(\PageIndex{2}\)

    Ejercicio\(\PageIndex{2}\): Card Sort: Proportional Relationships

    Tu profesor te dará 12 gráficas de relaciones proporcionales.

    1. Clasifica las gráficas en grupos en función de qué relación proporcional representan.
    2. Escribe una ecuación para cada relación proporcional diferente que encuentres.

    Ejercicio\(\PageIndex{3}\): Different Scales

    Dos grandes tanques de agua se están llenando de agua. El tanque A no se llena a una velocidad constante, y la relación entre su volumen de agua y tiempo se grafica en cada conjunto de ejes. El tanque B se llena a una tasa constante de\(\frac{1}{2}\) litros por minuto. La relación entre su volumen de agua y tiempo puede ser descrita por la ecuación\(v=\frac{1}{2}t\), donde\(t\) está el tiempo en minutos y\(v\) es el volumen total en litros de agua en el tanque.

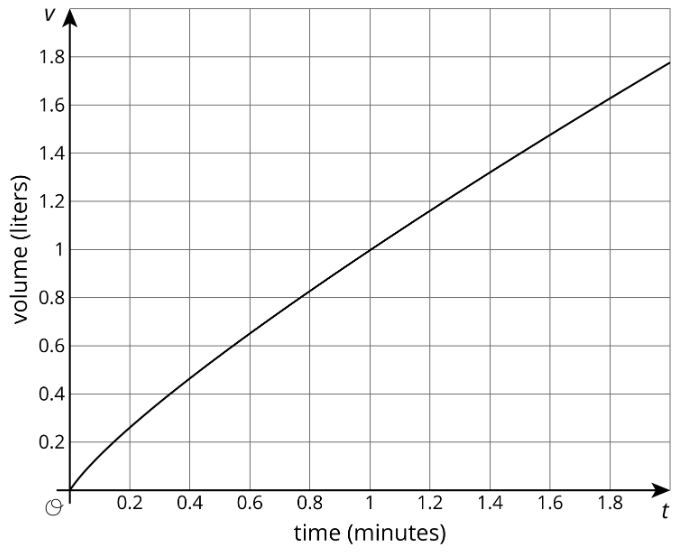
    clipboard_e92f2cca483bbdfc9af5a7bf6091f7b82.png
    Figura\(\PageIndex{3}\): Gráfico, eje horizontal, tiempo en minutos, escala 0 a 1 y 8 décimas, por 2 décimas de eje vertical, volumen en litros, 0 a 1 y 8 décimas, por 2 décimas de línea curva que pasa por origen, 1 coma 1 y 1 y 4 décimas coma 1 y 3 décimas.
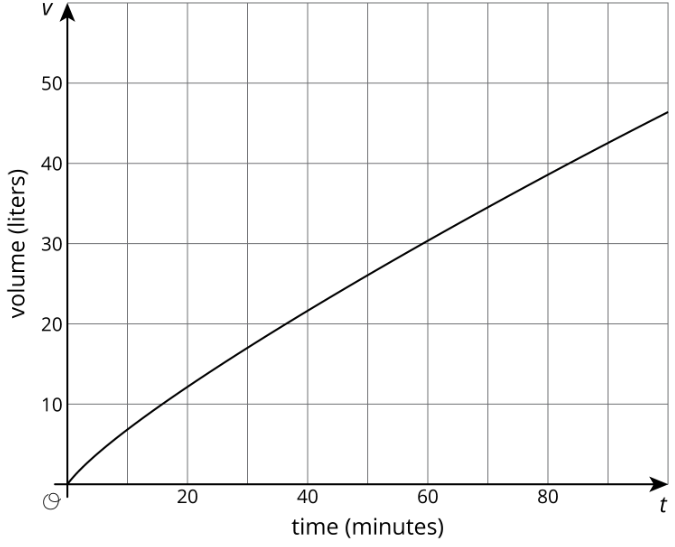
    clipboard_e80008d0a80fe779a7302f9053452b36b.png
    Figura\(\PageIndex{4}\): Gráfica, eje horizontal, tiempo en minutos, escala 0 a 80, por 20's. eje vertical, volumen en litros, 0 a 50, por 10's. línea curva que pasa por origen, 20 coma 12 y 60 coma 30.
    1. Dibuje y etiquete una gráfica de la relación entre el volumen de agua\(v\) y el tiempo\(t\) para el Tanque B en cada uno de los ejes.
    2. Responde las siguientes preguntas y di qué gráfico usaste para encontrar tu respuesta.
      1. Después de 30 segundos, ¿qué tanque tiene más agua?
      2. ¿En qué momentos aproximadamente ambos tanques tienen la misma cantidad de agua?
      3. ¿En qué momentos aproximadamente ambos tanques contienen 1 litro de agua? ¿20 litros?

    ¿Estás listo para más?

    Una tortuga gigante viaja a 0.17 millas por hora y una liebre ártica viaja a 37 millas por hora.

    1. Dibuje gráficas separadas que muestren la relación entre el tiempo transcurrido, en horas, y la distancia recorrida, en millas, tanto para la tortuga como para la liebre.
    2. ¿Sería útil tratar de poner ambas gráficas en el mismo par de ejes? ¿Por qué o por qué no?
    3. La tortuga y la liebre empiezan juntas y después de media hora la liebre se detiene a descansar. ¿Cuánto tiempo tarda la tortuga en ponerse al día?

    Resumen

    Las escalas que elegimos al graficar una relación a menudo dependen de qué información queremos saber. Por ejemplo, digamos que dos tanques de agua se llenan a diferentes velocidades constantes. La relación entre el tiempo en minutos\(t\) y el volumen en litros\(v\) del tanque A viene dada por\(v=2.2t\).

    Para el tanque B la relación es\(v=2.75t\).

    Estas ecuaciones nos dicen que el tanque A se está llenando a una velocidad constante de 2.2 litros por minuto y el tanque B se está llenando a una velocidad constante de 2.75 litros por minuto.

    Si queremos usar gráficas para ver en qué momentos los dos tanques tendrán 110 litros de agua, entonces usar una escala de eje de 0 a 10, como se muestra aquí, no es muy útil.

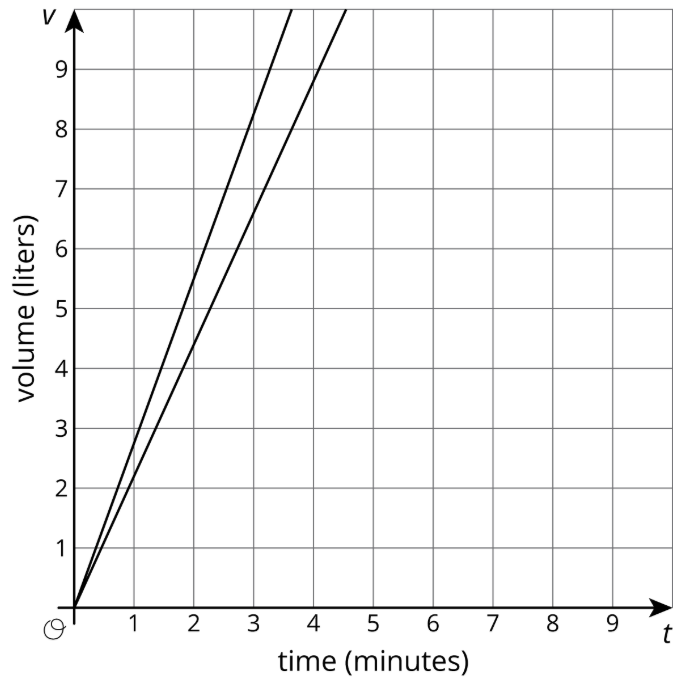
    clipboard_e62f6215aef00f94b8beee62a85fe2782.png
    Figura\(\PageIndex{5}\): Gráfica, eje horizontal, tiempo en minutos, escala 0 a 9, por 1's. eje vertical, volumen en litros, 0 a 9, por 1's. líneas, primera línea que pasa por origen y 2 comas 5 y 5 décimas. segunda línea pasando por origen y 2 comas 4 y 5 décimas.

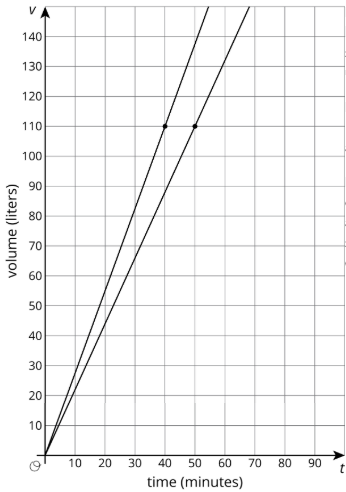
    Si utilizamos una escala vertical que va a 150 litros, un poco más allá de los 110 que estamos buscando, y una escala horizontal que va a los 100 minutos, obtenemos un conjunto de ejes mucho más útil para responder a nuestra pregunta.

    Ahora podemos ver que los dos tanques llegarán a 110 litros separados por 10 minutos: el tanque B después de 40 minutos de llenado y el tanque A después de 50 minutos de llenado.

    Es importante señalar que ambas gráficas son correctas, pero se usa un rango de valores que ayuda a responder la pregunta. Para elegir siempre una escala útil, debemos considerar la situación y las preguntas que se hacen al respecto.

    clipboard_effb046468d15db6f7d33325cf2421cc8.png
    Figura\(\PageIndex{6}\): Gráfica, eje horizontal, tiempo en minutos, escala 0 a 90, por 10's. eje vertical, volumen en litros, 0 a 140, por 10's. 2 líneas, primera línea pasando por origen y 40 coma 110. segunda línea pasando por origen y 50 coma 110.

    Entradas en el glosario

    Definición: Constante de proporcionalidad

    En una relación proporcional, los valores de una cantidad se multiplican cada uno por el mismo número para obtener los valores de la otra cantidad. A este número se le llama la constante de proporcionalidad.

    En este ejemplo, la constante de proporcionalidad es 3, porque\(2\cdot 3=6\),\(3\cdot 3=9\), y\(5\cdot 3=15\). Esto significa que hay 3 manzanas por cada 1 naranja en la ensalada de frutas.

    número de naranjas número de manzanas
    \(2\) \(6\)
    \(3\) \(9\)
    \(5\) \(15\)
    Mesa\(\PageIndex{1}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    La tortuga y la liebre están teniendo una carrera. Después de que la liebre corre 16 millas la tortuga sólo ha corrido 4 millas.

    La relación entre la distancia\(x\) que la tortuga “corre” en millas por cada\(y\) millas que corre la liebre es\(y=4x\). Grafica esta relación.

    clipboard_ef6979d8326a2dfa843434ced36ea4f1b.png
    Figura\(\PageIndex{7}\)

    Ejercicio\(\PageIndex{5}\)

    La tabla muestra una relación proporcional entre el peso en una escala de resorte y la distancia que el resorte ha estirado.

    1. Completa la tabla.
    2. Describe las escalas que podrías usar en los\(y\) ejes\(x\) y de una cuadrícula de coordenadas que mostraría todas las distancias y pesos en la tabla.
    distancia (cm) peso (newtons)
    \(20\) \(28\)
    \(55\)
    \(140\)
    \(1\)
    Mesa\(\PageIndex{2}\)

    Ejercicio\(\PageIndex{6}\)

    Encuentra una secuencia de rotaciones, reflexiones, traslaciones y dilataciones que muestren que una figura es similar a la otra. Sea específico: dar la cantidad y dirección de una traslación, una línea de reflexión, el centro y ángulo de una rotación, y el factor de centro y escala de una dilatación.

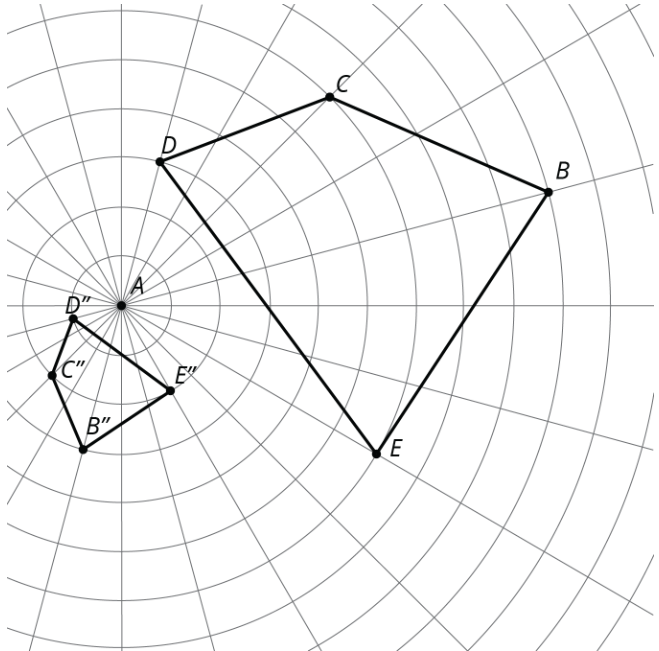
    clipboard_e74e99bd73ced1e8d8366e042fd48f961.png
    Figura\(\PageIndex{8}\): plano de coordenadas polares con centro en A. cuadrilátero BCDE y cuadrilátero B prima prima, C prima prima, D prima prima, E prima prima graficada. B a 9 coma pi sobre 12. C a 6 coma pi sobre 4. D a 3 coma 5 pi sobre 12, E a 6 coma 11 pi sobre 6. B primo primo a 3 coma 17 pi sobre 12. C prime prime a 2 coma 5 pi sobre 4. D prima prima a 1 coma 13 pi sobre 12. E prime prime a 2 coma 5 pi sobre 3.

    (De la Unidad 2.2.1)

    Ejercicio\(\PageIndex{7}\)

    Andre dijo: “Encontré dos figuras que son congruentes, así que no pueden ser similares”.

    Diego dijo: “¡No, son similares! El factor de escala es 1”.

    ¿Estás de acuerdo con alguno de ellos? Usa la definición de similitud para explicar tu respuesta.

    (De la Unidad 2.2.1)

    This page titled 3.1.2: Gráficas de Relaciones Proporcionales is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.