Saltar al contenido principal
LibreTexts Español

3.4.2: Más soluciones a ecuaciones lineales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118725

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lección

    Busquemos soluciones a ecuaciones más lineales.

    Ejercicio\(\PageIndex{1}\): Coordinate Pairs

    Para cada ecuación elija un valor para\(x\) y luego resuelva para encontrar el\(y\) valor correspondiente que haga que esa ecuación sea verdadera.

    1. \(6x=7y\)
    2. \(5x+3y=9\)
    3. \(y+5-\frac{1}{3}x=7\)

    Ejercicio\(\PageIndex{2}\): True or False: Solutions in the Coordinate Plane

    Aquí hay gráficas que representan tres relaciones lineales. Estas relaciones también podrían representarse con ecuaciones.

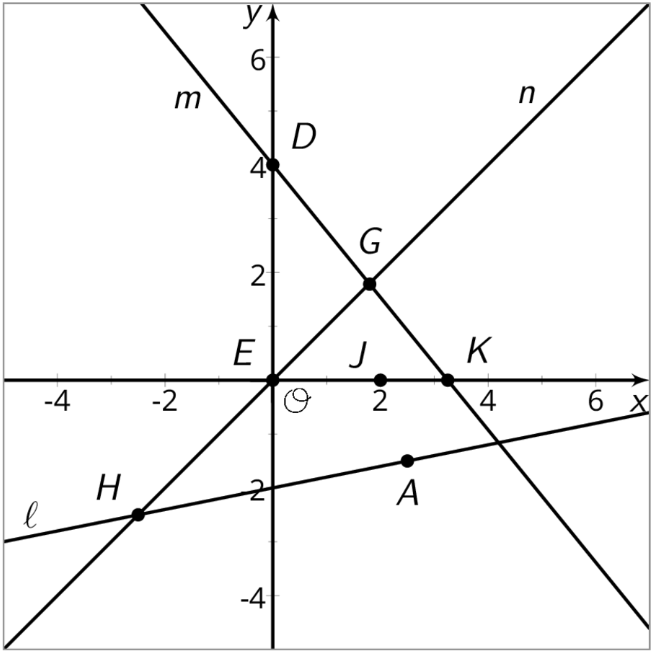
    clipboard_ee8408fb00d532d19619a49aa007c4526.png
    Figura\(\PageIndex{1}\): Gráfica, origen O, sin cuadrícula. Líneas l, m, n. Línea l, y interceptar -2. Línea m, y interceptar 4, etiquetada D. Línea n, e interceptar 0, etiquetada E. Punto A en la línea l. Punto H en las líneas l y n. Punto E en la línea n. Punto G en las líneas n y m. Punto K en la línea m. Punto J no en ninguna línea trazada a 2 coma 0.

    Para cada enunciado a continuación, decida si es verdadera o falsa. Explica tu razonamiento.

    1. \((4,0)\)es una solución de la ecuación para línea\(m\).
    2. Las coordenadas del punto\(G\) hacen que tanto las ecuaciones para línea\(m\) como la ecuación para línea\(n\) sean verdaderas.
    3. \(x=0\)es una solución de la ecuación para línea\(n\).
    4. \((2,0)\)hace que tanto la ecuación para línea\(m\) como la ecuación para línea sean\(n\) verdaderas.
    5. No hay solución para la ecuación para línea\(l\) que tiene\(y=0\).
    6. Las coordenadas de punto\(H\) son soluciones a las ecuaciones para línea\(l\).
    7. Hay exactamente dos soluciones de la ecuación por línea\(l\).
    8. Hay un punto cuyas coordenadas hacen verdaderas las ecuaciones de las tres líneas.

    Después de que termine de discutir las ocho declaraciones, busque otro grupo y verifique sus respuestas contra las suyas. Discutir cualquier desacuerdo.

    Ejercicio\(\PageIndex{3}\): I'll Take an X, Please

    Un compañero tiene 6 cartas etiquetadas de la A a la F y una pareja tiene 6 cartas etiquetadas de la a a la f. En cada par de cartas (por ejemplo, Cartas A y a), hay una ecuación en una carta y un par de coordenadas,\((x,y)\), que hace que la ecuación sea verdadera en la otra carta.

    1. El socio con la ecuación le pregunta al socio con una solución ya sea para el\(x\) -valor o el\(y\) -valor y explica por qué eligió el que hicieron.
    2. El socio con la ecuación utiliza este valor para encontrar el otro valor, explicando cada paso a medida que avanza.
    3. El compañero con el par de coordenadas le dice entonces al compañero con la ecuación si está bien o mal. Si se equivocan, ambos socios deben revisar los pasos para encontrar y corregir cualquier error. Si tienen razón, ambos socios pasan al siguiente juego de cartas.
    4. Sigue jugando hasta que hayas terminado las Cartas de la A a la F.

    ¿Estás listo para más?

    Considera la ecuación\(ax+by=c\), dónde\(a, b\), y\(c\) son números positivos.

    1. Encuentra las coordenadas de las\(y\) intercepciones\(x\) - y -de la gráfica de la ecuación.
    2. Encuentra la pendiente de la gráfica.

    Resumen

    Pensemos en la ecuación lineal\(2x-4y=12\). Si sabemos que\((0,-3)\) es una solución a la ecuación, entonces también sabemos que\((0,-3)\) es un punto en la gráfica de la ecuación. Dado que este punto está en el\(y\) eje -también sabemos que es la intercepción vertical de la gráfica. Pero, ¿qué pasa con la coordenada de la intercepción horizontal, cuándo\(y=0\)? Bueno, podemos usar la ecuación para resolverlo.

    \(\begin{aligned} 2x-4y&=12\\ 2x-4(0)&=12\\2x&=12\\x&=6\end{aligned}\nonumber\)

    Desde\(x=6\) cuando\(y=0\), sabemos que el punto\((6,0)\) está en la gráfica de la línea. No importa la forma en que venga una ecuación lineal, siempre podemos encontrar soluciones a la ecuación comenzando con un valor y luego resolviendo para el otro valor.

    Entradas en el glosario

    Definición: Solución a una ecuación con dos variables

    Una solución a una ecuación con dos variables es un par de valores de las variables que hacen que la ecuación sea verdadera.

    Por ejemplo, una posible solución a la ecuación\(4x+3y=24\) es\((6,0)\). Sustituir 6 por\(x\) y 0 por\(y\) hace que esta ecuación sea verdadera porque\(4(6)+3(0)=24\).

    Practica

    Ejercicio\(\PageIndex{4}\)

    Para cada ecuación, encuentra\(y\) cuándo\(x=-3\). Entonces encuentra\(x\) cuando\(y=2\)

    1. \(y=6x+8\)
    2. \(y=\frac{2}{3}x\)
    3. \(y=-x+5\)
    4. \(y=\frac{3}{4}x-2\frac{1}{2}\)
    5. \(y=1.5x+11\)

    Ejercicio\(\PageIndex{5}\)

    Verdadero o falso: Los puntos\((6,13)\),\((21,33)\), y\((99,137)\) todos se encuentran en la misma línea. La ecuación de la línea es\(y=\frac{4}{3}x+5\). Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{6}\)

    Aquí hay una ecuación lineal:\(y=\frac{1}{4}x+\frac{5}{4}\)

    1. ¿Son ((1,1.5)\) y\((12, 4)\) soluciones a la ecuación? Explica o muestra tu razonamiento.
    2. Encuentra la\(x\) -intercepción de la gráfica de la ecuación. Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{7}\)

    Encuentra las coordenadas de\(B\),\(C\), y\(D\) dado que\(AB=5\) y\(BC=10\).

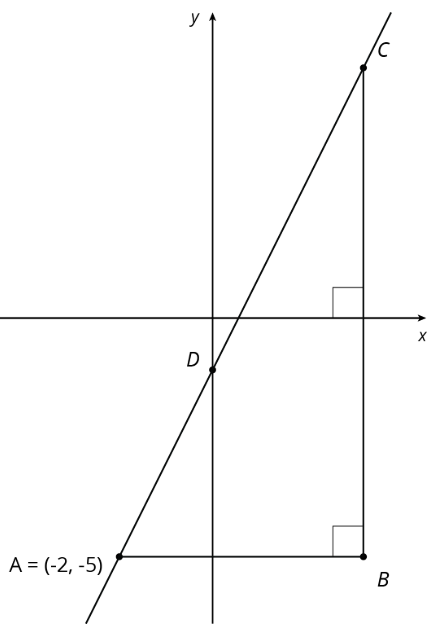
    clipboard_ea4d183953982453079ca92ee205dd4e3.png
    Figura\(\PageIndex{2}\): Línea graficada en plano xy sin cuadrículas. La línea pasa por el punto A en -2 coma -5, punto D, sin etiquetar en el eje y debajo del origen, y C, sin etiquetar en cuadrante 1. triángulo rectángulo dibujado desde el punto c, hacia abajo hasta el punto B, donde se ubica el ángulo recto, izquierda al punto A.

    (De la Unidad 2.3.2)

    Ejercicio\(\PageIndex{8}\)

    Hacer coincidir cada gráfica de una relación lineal con una situación que refleje más razonablemente su contexto.

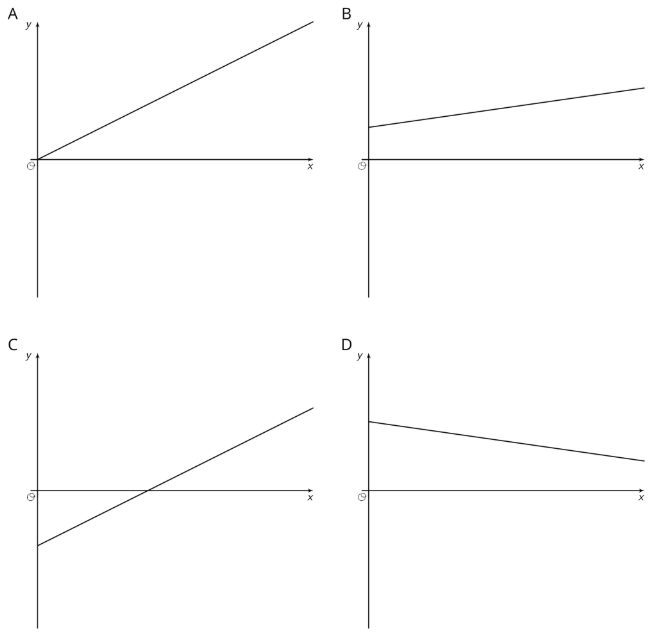
    clipboard_eaf626de8075a2b3a4a3c3b2864fd3440.png
    Figura\(\PageIndex{3}\): 4 gráficas de líneas etiquetadas A, B, C. D. A, y intercept = 0, pendiente positiva. B, y intercepción = pendiente positiva, pendiente positiva, menos empinada que A. C, y intercepción = pendiente negativa, positiva. D, y intercepción = positivo, pendiente = negativo.
    1. Gráfica A
    2. Gráfica B
    3. Gráfica C
    4. Gráfica D
    1. \(y\)es el peso de un gatito\(x\) días después del nacimiento.
    2. \(y\)es la distancia que queda para recorrer en un viaje en automóvil después de\(x\) horas de manejo a un ritmo constante hacia su destino.
    3. \(y\)es la temperatura, en grados C, de un gas que se calienta en un experimento de laboratorio.
    4. \(y\)es la cantidad de calorías consumidas comiendo\(x\) galletas saladas.

    (De la Unidad 3.3.1)

    This page titled 3.4.2: Más soluciones a ecuaciones lineales is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.