4.2.7: ¿Cuántas soluciones?

Lección

Resolvamos ecuaciones con diferentes números de soluciones.

Ejercicio\(\PageIndex{1}\): Matching Solutions

Considera la ecuación inconclusa\(12(x-3)+18=\underline{ }\). Coincidir las siguientes expresiones con el número de soluciones que tendría la ecuación con esa expresión en el lado derecho.

1. \(6(2x-3)\)
2. \(4(3x-3)\)
3. \(4(2x-3)\)

• una solución
• no hay soluciones
• todas las soluciones

Ejercicio\(\PageIndex{2}\): Thinking About Solutions Some More

Tu profesor te dará algunas tarjetas.

1. Con tu pareja, resuelve cada ecuación.
2. Después, ordenarlos en categorías.
3. Describe las características definitorias de esas categorías y prepárate para compartir tu razonamiento con la clase.

Ejercicio\(\PageIndex{3}\): Make Use of Structure

Para cada ecuación, determine si no tiene soluciones, exactamente una solución, o es cierto para todos los valores de\(x\) (y tiene infinitamente muchas soluciones). Si una ecuación tiene una solución, resuelva para encontrar el valor de\(x\) eso hace que la afirmación sea verdadera.

1. 1. \(6x+8=7x+13\)
   2. \(6x+8=2(3x+4)\)
   3. \(6x+8=6x+13\)
2. 1. \(\frac{1}{4}(12-4x)=3-x\)
   2. \(x-3=3-x\)
   3. \(x-3=3+x\)
3. 1. \(-5x-3x+2=-8x+2\)
   2. \(-5x-3x-4=-8x+2\)
   3. \(-5x-4x-2=-8x+2\)
4. 1. \(4(2x-2)+2=4(x-2)\)
   2. \(4x+2(2x-3)=8(x-1)\)
   3. \(4x+2(2x-3)=4(2x-2)+2\)
5. 1. \(x-3(2-3x)=2(5x+3)\)
   2. \(x-3(2+3x)=2(5x-3)\)
   3. \(x-3(2-3x)=2(5x-3)\)
6. ¿Qué notas acerca de las ecuaciones con una sola solución? ¿En qué se diferencia esto de las ecuaciones sin soluciones y ecuaciones que son ciertas para cada una\(x\)?

¿Estás listo para más?

Los números consecutivos siguen uno tras otro. Un ejemplo de tres números consecutivos es 17, 18 y 19. Otro ejemplo es -100, -99, -98.

1. Elija cualquier conjunto de tres números consecutivos. Encuentra su promedio. ¿Qué notas?
2. Encuentra el promedio de otro conjunto de tres números consecutivos. ¿Qué notas?
3. Explica por qué lo que notaste siempre debe funcionar, o encontrar un contraejemplo.

Resumen

A veces es posible mirar la estructura de una ecuación y decir si tiene infinitamente muchas soluciones o ninguna solución. Por ejemplo, mira

\[2(12x+18)+6=18x+6(x+7)\nonumber\].

Usando la propiedad distributiva en los lados izquierdo y derecho, obtenemos

\[24x+36+6=18x+6x+42\nonumber\].

A partir de aquí, coleccionar términos similares nos da

\[24x+42=24x+42\nonumber\].

Ya que los lados izquierdo y derecho de la ecuación son los mismos, sabemos que esta ecuación es cierta para cualquier valor de ¡\(x\)sin hacer más movimientos!

Del mismo modo, a veces podemos usar la estructura para saber si una ecuación no tiene soluciones. Por ejemplo, mira

\[6(6x+5)=12(3x+2)+12\nonumber\].

Si pensamos en cada movimiento a medida que avanzamos, podemos detenernos cuando nos demos cuenta de que no hay solución:

\[\begin{aligned} \frac{1}{6}\cdot 6(6x+5)&=\frac{1}{6}\cdot (12(3x+2)+12) &\text{Multiply each side by }\frac{1}{6}. \\ 6x+5&=2(3x+2)+2 &\text{Distribute }\frac{1}{6}\text{ on the right side.} \\ 6x+5&=6x+4+2 &\text{Distribute 2 on the right side.}\end{aligned}\nonumber\]

El último movimiento deja claro que los términos constantes en cada lado, 5 y\(4+2\), no son los mismos. Dado que sumar 5 a una cantidad siempre es menor que\(4+2\) sumar a esa misma cantidad, sabemos que no hay soluciones.

Hacer movimientos para mantener una ecuación equilibrada es una parte poderosa de la resolución de ecuaciones, pero pensar en lo que la estructura de una ecuación nos dice sobre las soluciones es igual de importante.

Entradas en el glosario

Definición: Coeficiente

Un coeficiente es un número que se multiplica por una variable.

Por ejemplo, en la expresión\(3x+5\), el coeficiente de\(x\) es 3. En la expresión\(y+5\), el coeficiente de\(y\) es 1, porque\(y=1\cdot y\).

Definición: Término constante

En una expresión como\(5x+2\), el número 2 se llama término constante porque no cambia cuando\(x\) cambia.

En la expresión\(7x+9\), 9 es el término constante.
En la expresión\(5x+(-8)\), -8 es el término constante.
En la expresión\(12-4x\), 12 es el término constante.

Definición: Término

Un término es parte de una expresión. Puede ser un solo número, una variable, o un número y una variable que se multiplican entre sí. Por ejemplo, la expresión\(5x+18\) tiene dos términos. El primer término es\(5x\) y el segundo es 18.

Practica

Ejercicio\(\PageIndex{4}\)

Lin estaba mirando la ecuación\(2x-32+4(3x-2462)=14x\). Ella dijo: “Puedo decir de inmediato que no hay soluciones, porque en el lado izquierdo, vas a tener\(2x+12x\) y un montón de constantes, pero tienes justo del\(14x\) lado derecho”. ¿Estás de acuerdo con Lin? Explica tu razonamiento.

Ejercicio\(\PageIndex{5}\)

Han estaba mirando la ecuación\(6x-4+2(5x+2)=16x\). Dijo: “Puedo decir de inmediato que no hay soluciones, porque del lado izquierdo, vas a tener\(6x+10x\) y un montón de constantes, pero tienes justo del\(16x\) lado derecho”. ¿Estás de acuerdo con Han? Explica tu razonamiento.

Ejercicio\(\PageIndex{6}\)

Decidir si cada ecuación es verdadera para todos, uno, o ningún valor de\(x\).

1. \(6x=-4=-4+6x\)
2. \(4x-6=4x+3\)
3. \(-2x+4=-3x+4\)

Ejercicio\(\PageIndex{7}\)

Resuelve cada una de estas ecuaciones. Explica o muestra tu razonamiento.

1. \(3(x-5)=6\)
2. \(2(x-\frac{2}{3})=0\)
3. \(4x-5=2-x\)

(De la Unidad 4.2.3)

Ejercicio\(\PageIndex{8}\)

Los puntos\((-2,0)\) y\((0,-6)\) están cada uno en la gráfica de una ecuación lineal. ¿\((2,6)\)También está en la gráfica de esta ecuación lineal? Explica tu razonamiento.

(De la Unidad 3.4.2)

Ejercicio\(\PageIndex{9}\)

En la imagen triángulo\(A'B'C'\) es una imagen de triángulo\(ABC\) después de una rotación. El centro de rotación es\(E\).

Figura\(\PageIndex{1}\)

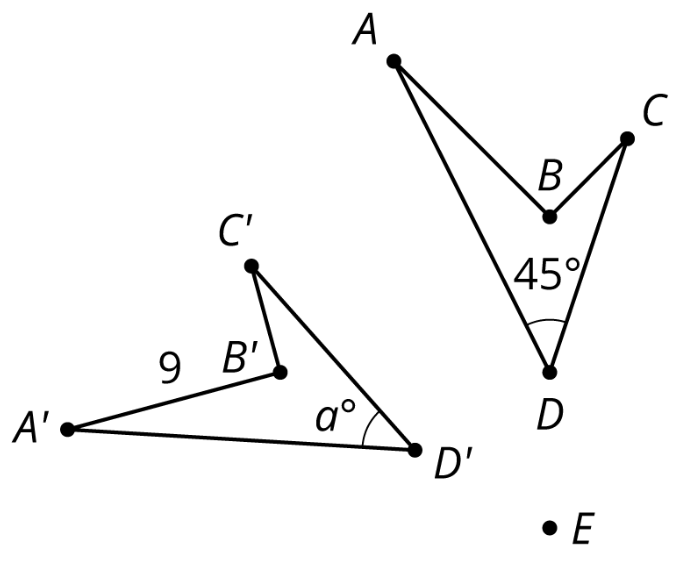
1. ¿Cuál es la longitud del lado\(AB\)? Explique cómo sabe.
2. ¿Cuál es la medida del ángulo\(D'\)? Explique cómo sabe.

(De la Unidad 1.2.1)