4.3.1: ¿Encendido o Fuera de Línea?

Última actualización
Guardar como PDF

Page ID: 118687

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Interpretemos el significado de los puntos en un plano de coordenadas.

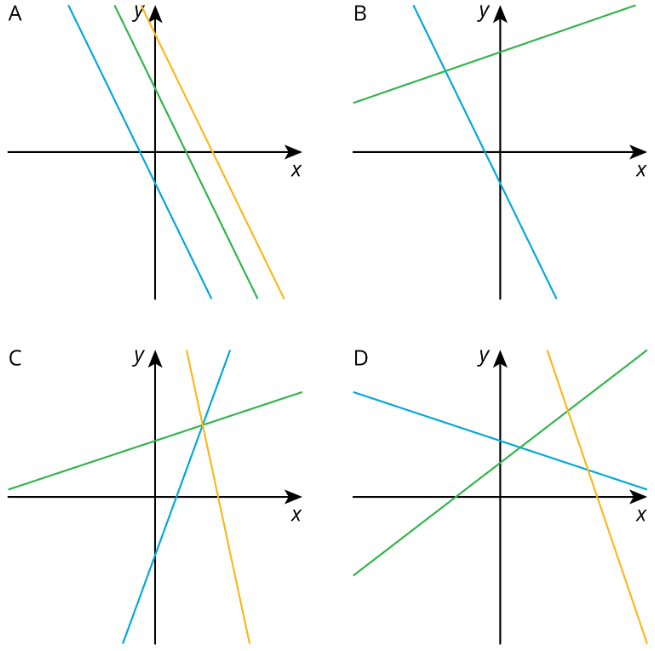
Ejercicio$\PageIndex{1}$: Which One Doesn't Belong: Lines in the Plane

¿Cuál no pertenece? Explica tu razonamiento.

Figura$\PageIndex{1}$: Cuatro gráficas, cada una en el plano x y. Gráfica A. 3 líneas que no se cruzan. Una línea cruza el eje x a la izquierda del origen y el eje y debajo del origen. Otra línea cruza el eje y por encima del origen y el eje x a la derecha del origen. La tercera línea cruza el eje y por encima del origen y el eje x a la derecha del origen. Gráfica B. 2 líneas de intersección. Una línea cruza el eje x a la izquierda del origen y el eje y debajo del origen. Otra línea cruza el eje y por encima del origen. Gráfica C. Tres líneas que se cruzan en un solo punto. Una línea cruza el eje y por encima del origen. Otra línea cruza el eje x a la derecha del origen y el eje y debajo del origen. La tercera línea cruza el eje x a la derecha del origen. Gráfica D. Tres líneas. Hay 3 puntos de intersección entre dos líneas cada uno. Una línea cruza el eje y por encima del origen. Otra línea cruza el eje x a la izquierda del origen y el eje y por encima del origen. La tercera línea cruza el eje x a la derecha del origen.

Ejercicio$\PageIndex{2}$: Pocket Full of Change

Jada le dijo a Noah que tiene 2 dólares en cuartos y monedas de diez centavos en su bolsillo y 17 monedas todas juntas. Ella le pidió que adivinara cuántos de cada tipo de moneda tiene.

Aquí hay una tabla que muestra algunas combinaciones de cuartos y diez centavos que valen $2. Completa la tabla.

Mesa$\PageIndex{1}$
número de cuartos	número de dimes
$0$	$20$
$4$
	$0$
	$5$

Aquí hay una gráfica de la relación entre el número de cuartos y el número de monedas de diez centavos cuando hay un total de 17 monedas.
1. W sombrero hace punto$A$ represent?
2. ¿Cuánto dinero, en dólares,$A$ vale la combinación representada por Point?

Figura$\PageIndex{2}$: Gráfica de puntos en el plano x y, origen O, con cuadrícula. Eje horizontal, número de cuartos, escala 0 a 24 por 1s. Eje vertical, número de dimes, escala 0 a 24 por 1s. Los puntos trazados son 0 coma 17, 1 coma 16, 2 coma 15, 3 coma 14, 4 coma 13, 5 coma 12, 6 coma 11, 7 coma 10, 8 coma 9 etiquetada A, 9 coma 8, 10 coma 7, 11 coma 6, 12 coma 5, 13 coma 4, 14 coma 3, 15 coma 2, 16 coma 1 y 17 ma 0.

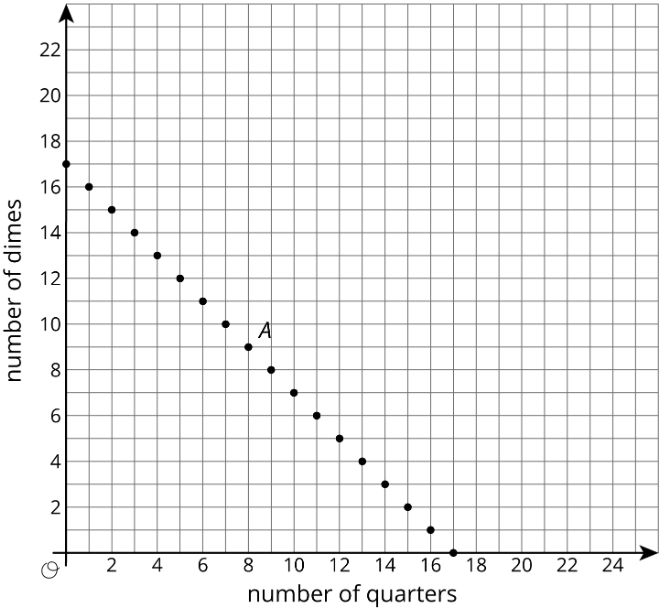
3. ¿Es posible que Jada tenga 4 cuartos y 13 centavos en el bolsillo? Explica cómo sabes.

4. ¿Cuántos cuartos y diez minutos debe tener Jada? Explica tu razonamiento.

Ejercicio$\PageIndex{3}$: Making Signs

Clare y Andre están haciendo carteles para todos los casilleros como parte de las decoraciones para la próxima semana del espíritu. El día de ayer, Andre hizo 15 señales y Clare hizo 5 señales. Hoy en día, necesitan hacer más señales. El progreso de cada persona hoy se muestra en el plano de coordenadas.

Figura$\PageIndex{3}$: Gráfica de dos líneas en el plano x y, origen 0, con cuadrícula. Eje horizontal, tiempo en minutos, escala 0 a 110, por 5s. Eje vertical, número de señales terminadas, escala 0 a 70 por 5s. Una línea cruza el eje y en 5 y pasa por los puntos A y B. Otra línea cruza el eje y en 15 y pasa por los puntos C y A. Comenzando en el origen, el punto A es 8 unidades a la derecha y 5 unidades hacia arriba. Comenzando por el origen, el punto B está 15 unidades a la derecha y 8 punto 5 unidades arriba. Comenzando por el origen, el punto C es 0 unidades a la derecha, y 3 unidades arriba. Comenzando por el origen, el punto D está 20 unidades a la derecha y 12 unidades hacia arriba.

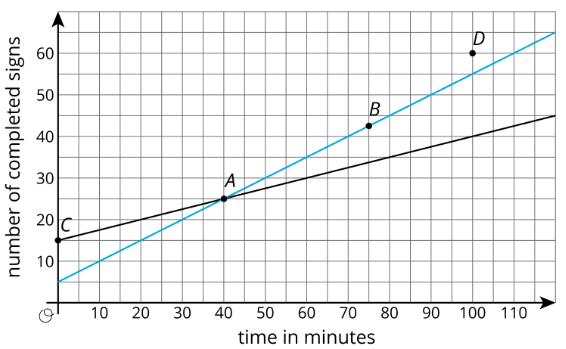
Con base en las líneas, marcar las declaraciones como verdaderas o falsas para cada persona.

Mesa$\PageIndex{2}$
punto	lo que dice	Clare	Andre
$A$	A los 40 minutos, tengo 25 señales terminadas.
$B$	A los 75 minutos, tengo 42 señales y media terminadas.
$C$	A los 0 minutos, tengo 15 señales terminadas.
$D$	A los 100 minutos, tengo 60 señales terminadas.

¿Estás listo para más?

4 palillos hacen 1 cuadrado
7 palillos hacen 2 cuadrados
10 palillos hacen 3 cuadrados

¿Ves un patrón? Si es así, ¿cuántos mondadientes necesitarías para hacer 10 cuadrados de acuerdo a tu patrón? ¿Puedes representar tu patrón con una expresión?

Resumen

Se estudiaron las relaciones lineales en una unidad anterior. Aprendimos que los valores de$x$ y$y$ que hacen que una ecuación sea verdadera corresponden a puntos$(x,y)$ en la gráfica. Por ejemplo, si tenemos$x$ libras de harina que cuestan $0.80 por libra y$y$ libras de azúcar que cuestan $0.50 por libra, y el costo total es de $9.00, entonces podemos escribir una ecuación como esta para representar la relación entre$x$ y$y:$

$0.8x+0.5y=9$

Ya que 5 libras de harina cuesta $4.00 y 10 libras de azúcar cuesta $5.00, lo sabemos$x=5$,$y=10$ es una solución a la ecuación, y el punto$(5,10)$ es un punto en la gráfica. La línea que se muestra es la gráfica de la ecuación:

Figura$\PageIndex{5}$: La gráfica de una línea en el plano x y. La línea se inclinó hacia abajo y hacia la derecha, cruza el eje y en 18, y pasa por el punto 5 coma 10. Dos puntos adicionales, 9 coma 16 y 1 coma 14, están etiquetados en la gráfica.

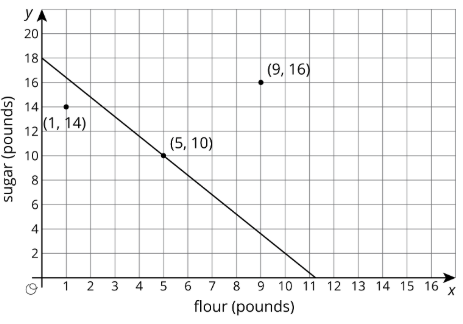
Observe que se muestran dos puntos que no están en la línea. ¿Qué significan en el contexto? El punto$(1,14)$ significa que hay 1 libra de harina y 14 libras de azúcar. El costo total para esto es$(0.8\cdot 1+0.5\cdot 14$ o $7.80. Dado que el costo no es de $9.00, este punto no está en la gráfica. De igual manera, 9 libras de harina y 16 libras de azúcar cuestan$0.8\cdot 9+0.5\cdot 16$ o $15.20, por lo que el otro punto tampoco está en la gráfica.

Supongamos que también sabemos que la harina y el azúcar juntos pesan 15 libras. Esto significa que

$x+y=15$

Si dibujamos la gráfica de esta ecuación en el mismo plano de coordenadas, vemos que pasa por dos de los tres puntos etiquetados:

Figura$\PageIndex{6}$: La gráfica de dos líneas que se cruzan en el plano x y. La primera línea se inclinó hacia abajo y hacia la derecha, cruza el eje y en 18, y pasa por el punto 5 coma 10. La segunda línea se inclinó hacia abajo y hacia la derecha y pasa por los puntos 1 coma 14 y 5 coma 10. Un punto adicional, 9 coma 16, está etiquetado en la gráfica.

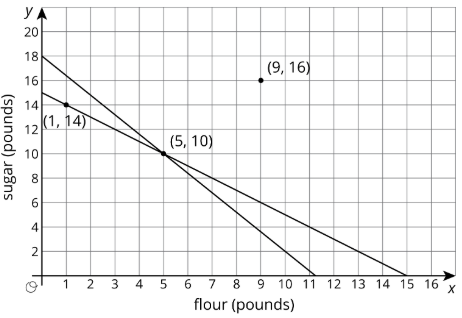
El punto$(1,14)$ está en la gráfica de$x+y=15$ porque$1+14=15$. De igual manera,$5+10=15$. Pero$9+16\neq 15$, así no$(9,16)$ está en la gráfica de$x+y=15$. En general, si tenemos dos líneas en el plano de coordenadas,

Las coordenadas de un punto que está en ambas líneas hacen que ambas ecuaciones sean verdaderas.
Las coordenadas de un punto en una sola línea hacen que una sola ecuación sea verdadera.
Las coordenadas de un punto en ninguna línea hacen que ambas ecuaciones sean falsas.

Practica

Ejercicio$\PageIndex{4}$

1. Coincidir las líneas$m$ y$n$ con las declaraciones que representan:

Figura$\PageIndex{7}$: Dos líneas en un plano x y. La línea m pasa por los puntos E, B y D. El punto E está en 13 coma 3. El punto B está en 6 coma negativo 4. El punto D está en 2 coma negativa 8. La línea n pasa por los puntos A, B y C. El punto A está en negativo 2 coma 4. El punto B está en 6 coma negativo 4. El punto C está en 12 coma negativa 10.

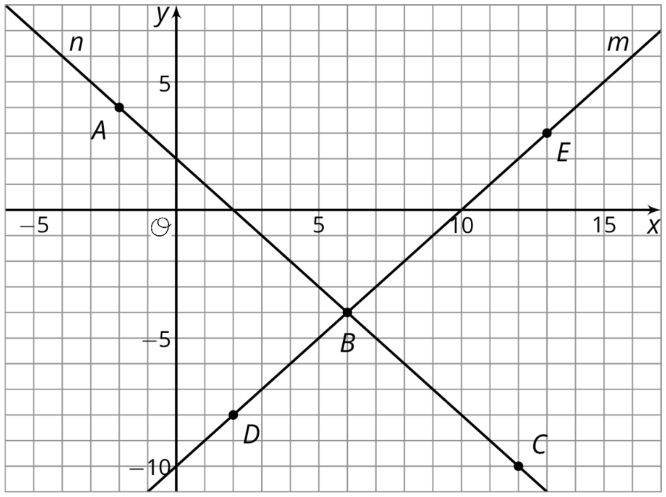
Un conjunto de puntos donde las coordenadas de cada punto tienen una suma de 2
Un conjunto de puntos donde la$y$ coordenada -de cada punto es 10 menor que su$x$ coordenada -

2. Haga coincidir los puntos etiquetados en la gráfica con declaraciones sobre sus coordenadas:

Dos números con una suma de 2
Dos números donde la$y$ coordenada -es 10 menor que la$x$ coordenada -
Dos números con una suma de 2 y donde la$y$ coordenada -es 10 menor que la$x$ coordenada -

Ejercicio$\PageIndex{5}$

Aquí hay una ecuación:$4x-4=4x+\underline{ }$. ¿Qué podrías escribir en el espacio en blanco para que la ecuación sea cierta para:

No hay valores de$x$
Todos los valores de$x$
Un valor de$x$

(De la Unidad 4.2.6)

Ejercicio$\PageIndex{6}$

Mai gana 7 dólares por hora cortando el césped de sus vecinos. También ganó 14 dólares por transportar bolsas de reciclables para algunos vecinos.

Priya cuida a los hijos de su vecina. En la tabla se muestra la cantidad de dinero$m$ que gana en$h$ horas. Priya y Mai han accedido a ir al cine el fin de semana después de que hayan ganado la misma cantidad de dinero por el mismo número de horas de trabajo.

Mesa$\PageIndex{3}$
$h$	$m$
\ (h\) ">$1$	\ (m\) ">$$8.40$
\ (h\) ">$2$	\ (m\) ">$$16.80$
\ (h\) ">$4$	\ (m\) ">$$33.60$

¿Cuántas horas tienen que trabajar cada uno antes de ir al cine?
¿Cuánto habrá ganado cada uno de ellos?
Explique dónde se puede ver la solución en tablas de valores, gráficas y ecuaciones que representan las ganancias por hora de Priya y Mai.

Ejercicio$\PageIndex{7}$

Para cada ecuación, explica lo que podrías hacer primero a cada lado de la ecuación para que no hubiera fracciones. No tienes que resolver las ecuaciones (a menos que quieras más práctica).

$\frac{3x-4}{8}=\frac{x+2}{3}$
$\frac{3(2-4)}{4}=\frac{3+r}{6}$
$\frac{4p+3}{8}=\frac{p+2}{4}$
$\frac{2(a-7)}{15}=\frac{a+4}{6}$

(De la Unidad 4.2.5)

Ejercicio$\PageIndex{8}$

El dueño de un nuevo restaurante está ordenando mesas y sillas. Quiere tener solo mesas para 2 y mesas para 4. El número total de personas que se pueden sentar en el restaurante es de 120.

Describa algunas combinaciones posibles de mesas de 2 asientos y mesas de 4 asientos con capacidad para 120 clientes. Explica cómo los encontraste.
Escribir una ecuación para representar la situación. ¿Qué representan las variables?
Crear una gráfica para representar la situación.

4. ¿Qué nos dice la pendiente de la situación?

5. Interpretar el$x$ e$y$ interceptar en la situación.

(De la Unidad 3.5.1)

número de cuartos	número de dimes
\(0\)	\(20\)
\(4\)
	\(0\)
	\(5\)

\(h\)	\(m\)
\ (h\) ">\(1\)	\ (m\) ">\($8.40\)
\ (h\) ">\(2\)	\ (m\) ">\($16.80\)
\ (h\) ">\(4\)	\ (m\) ">\($33.60\)

Search

Text Color

Text Size

Margin Size

Font Type

punto	lo que dice	Clare	Andre
\(A\)	A los 40 minutos, tengo 25 señales terminadas.
\(B\)	A los 75 minutos, tengo 42 señales y media terminadas.
\(C\)	A los 0 minutos, tengo 15 señales terminadas.
\(D\)	A los 100 minutos, tengo 60 señales terminadas.