4.3.2: En ambas líneas

Última actualización
Guardar como PDF

Page ID: 118690

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lección

Usemos líneas para pensar en situaciones.

Ejercicio$\PageIndex{1}$: Notice and Wonder: Bugs Passing in the Night

Figura$\PageIndex{1}$: Cuatro líneas numérica en blanco. Cada línea numérica tiene una mariquita orientada hacia la derecha y una hormiga hacia la izquierda. La línea número 1 está etiquetada como inicio de mariquita en el extremo izquierdo y 0 segundos. La mariquita está a la izquierda de la recta numérica y la hormiga está a la derecha de la recta numérica. La línea numérica 2 está etiquetada con 2 segundos. La mariquita se encuentra en la octava marca de la derecha. La hormiga está en la marca 16 de la izquierda. La línea numérica 3 está etiquetada como 4 segundos. La mariquita está en la marca 16 de la derecha. La hormiga se encuentra en la marca 32 de la izquierda. La línea numérica 4 está etiquetada con 6 segundos. La mariquita está en la marca 24. La hormiga no se muestra en la recta numérica.

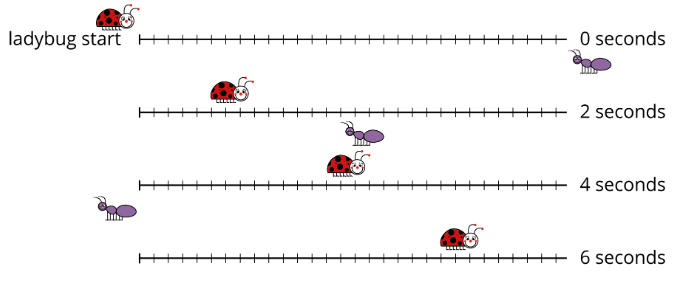
Ejercicio$\PageIndex{2}$: Bugs Passing in the Night, Continued

Una hormiga y una mariquita diferentes están a cierta distancia, y empiezan a caminar la una hacia la otra. La gráfica muestra la distancia de la mariquita desde su punto de partida a lo largo del tiempo y el punto etiquetado$(2.5,10)$ indica cuándo la hormiga y la mariquita se pasan entre sí.

Figura$\PageIndex{2}$: Gráfica de una línea, origen O, con cuadrícula. Eje horizontal, tiempo en segundos, escala 0 a 5, por 1's. Eje vertical, distancia en centímetros, escala 0 a 24, por 2's. La línea pasa por el origen y el punto 2 punto 5 coma 10.

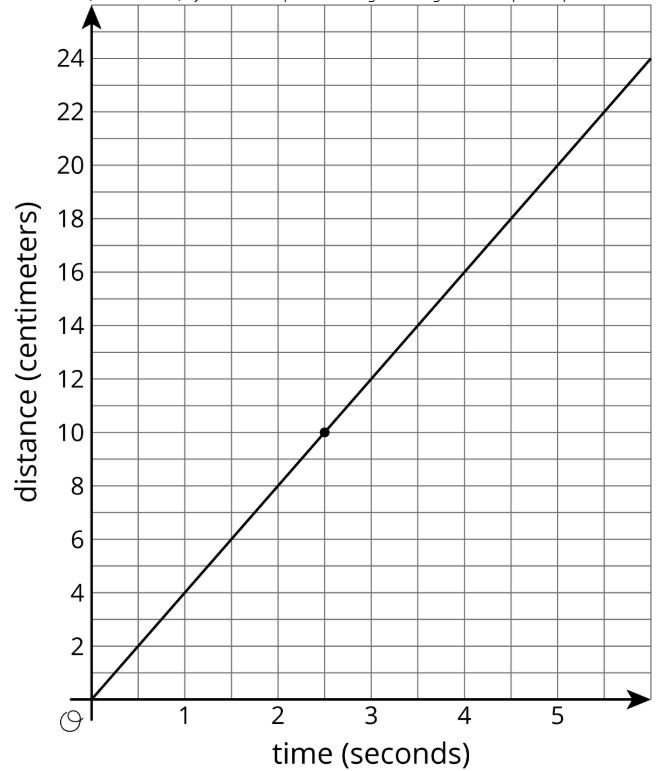
La hormiga está caminando 2 centímetros por segundo.

Escribir una ecuación que represente la relación entre la distancia de la hormiga desde el punto de partida de la mariquita y la cantidad de tiempo que ha pasado.
Si aún no lo has hecho, dibuja la gráfica de tu ecuación en el mismo plano de coordenadas.

Ejercicio$\PageIndex{3}$: A Close Race

Elena y Jada corrían 100 metros en sus bicicletas. Ambos corredores comenzaron al mismo tiempo y cabalgaron a velocidad constante. Aquí hay una tabla que da información sobre la carrera de bicicletas de Jada:

Mesa$\PageIndex{1}$
tiempo desde el inicio (segundos)	distancia desde el inicio (metros)
$6$	$36$
$9$	$54$

1. Grafica la relación entre distancia y tiempo para la carrera ciclista de Jada. Asegúrese de etiquetar y escalar los ejes de manera apropiada.

2. Elena recorrió toda la carrera a 6 metros constantes por segundo. En el mismo conjunto de ejes, grafica la relación entre distancia y tiempo para la carrera ciclista de Elena.

3. ¿Quién ganó la carrera?

Resumen

Las soluciones a una ecuación corresponden a puntos en su gráfica. Por ejemplo, si el Auto A viaja 75 millas por hora y pasa por un área de descanso cuando$t=0$, entonces la distancia en millas que ha recorrido desde el área de descanso después de$t$ horas es

$d=75t$

El punto$(2,150)$ está en la gráfica de esta ecuación porque$150=75\cdot 2$: dos horas después de pasar la zona de descanso, el automóvil ha recorrido 150 millas.

Si tienes dos ecuaciones, puedes preguntar si hay un par ordenado que sea una solución para ambas ecuaciones simultáneamente. Por ejemplo, si el Auto B viaja hacia el área de descanso y su distancia del área de descanso es

$d=14-65t$

Podemos preguntar si alguna vez hay un momento en que la distancia del Auto A del área de descanso sea la misma que la distancia del Auto B del área de descanso. Si la respuesta es “sí”, entonces la solución corresponderá a un punto que está en ambas líneas.

Figura$\PageIndex{4}$: Gráfica de 2 líneas, origen O, con cuadrícula. Eje horizontal, tiempo en horas, escala 0 al punto 22, por punto 0 2's. eje vertical, distancia en millas, escala 0 a 14, por 2's. Una línea pasa por el origen y el punto 0 punto 1 coma 7 punto 5. Otra línea cruza el eje y en 14 y pasa por el punto 0 punto 1 coma 7 punto 5.

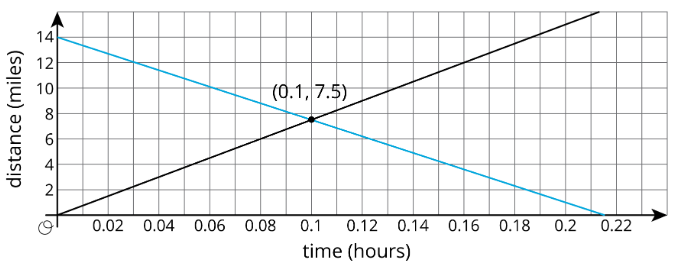
Al observar las coordenadas del punto de intersección, vemos que el Auto A y el Coche B estarán ambos a 7.5 millas del área de descanso después de 0.1 horas (que es de 6 minutos).

Ahora supongamos que otro automóvil, el Auto C, también había pasado la parada de descanso en su momento$t=0$ y viajó en la misma dirección que el Auto A, yendo también 75 millas por hora. Su ecuación también lo sería$d=75t$. Cualquier solución a la ecuación para Car A también sería una solución para Car C, y cualquier solución a la ecuación para Car C también sería una solución para Car A. La línea para Car C aterrizaría justo encima de la línea para Car A. En este caso, cada punto de la línea gráfica es una solución a ambas ecuaciones, de manera que ahí son infinitamente muchas soluciones a la pregunta “¿cuándo el Auto A y el Coche C están a la misma distancia de la parada de descanso?” Esto significaría que el Coche A y el Coche C estuvieron uno al lado del otro durante todo su viaje.

Cuando tenemos dos ecuaciones lineales que son equivalentes entre sí, como$y=3x+2$ y$2y=6x+4$, obtendremos dos líneas que están “justo encima” una de la otra. Cualquier solución a una ecuación también es solución a la otra, por lo que estas dos líneas se cruzan en infinitamente muchos puntos.

Practica

Ejercicio$\PageIndex{4}$

Diego tiene $11 y comienza a ahorrar $5 cada semana para comprar un nuevo teléfono. Al mismo tiempo que Diego comienza a ahorrar, Lin tiene 60 dólares y comienza a gastar 2 dólares semanales en suministros para su clase de arte. ¿Hay una semana en la que tengan la misma cantidad de dinero? ¿Cuánto tienen en ese momento?

Ejercicio$\PageIndex{5}$

Usa una gráfica para encontrar$x$ y$y$ valores que hacen que ambos$y=\frac{-2}{3}x+3$ y sean$y=2x-5$ verdaderos.

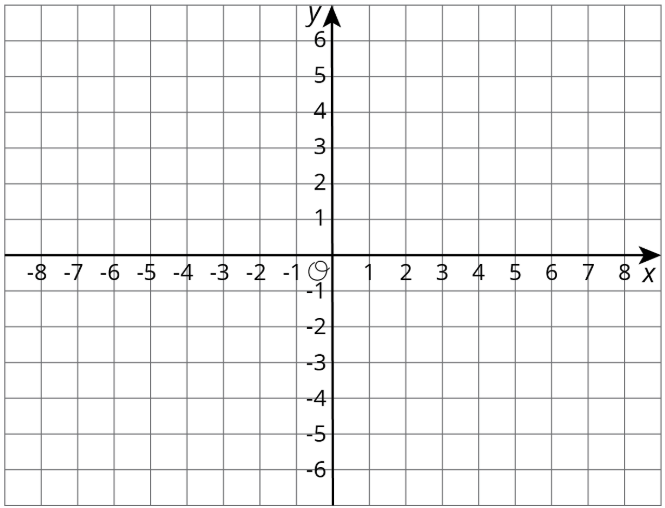
Ejercicio$\PageIndex{6}$

El punto donde se cruzan las gráficas de dos ecuaciones tiene$y$ -coordenada 2. Una ecuación es$y=-3x+5$. Encuentra la otra ecuación si su gráfica tiene una pendiente de 1.

Ejercicio$\PageIndex{7}$

Una granja tiene gallinas y vacas. Todas las vacas tienen 4 patas y todas las gallinas tienen 2 patas. Todos juntos, hay 82 patas de vaca y pollo en la granja. Completa la tabla para mostrar algunas combinaciones posibles de pollos y vacas para obtener 82 patas en total.

Mesa$\PageIndex{2}$
número de pollos ($x$)	número de vacas ($y$)
\ (x\)) ">$35$	\ (y\)) ">
\ (x\)) ">$7$	\ (y\)) ">
\ (x\)) ">	\ (y\)) ">$10$
\ (x\)) ">$19$	\ (y\)) ">
\ (x\)) ">	\ (y\)) ">$5$

Aquí hay una gráfica que muestra posibles combinaciones de pollos y vacas que suman hasta 30 animales:

Figura$\PageIndex{6}$: Gráfica de puntos en el plano x y, origen O, con cuadrícula. Eje horizontal, número de pollos, escala 0 a 30 por 1s. Eje vertical, número de vacas, escala 0 a 30 por 1s. Los puntos trazados son 0 coma 30, 1 coma 29, 2 coma 28, 3 coma 27, 4 coma 26, 5 coma 25, 6 coma 24, 7 coma 23, 8 coma 22, 9 coma 21, 10 coma 20, 11 coma 19, 12 coma 18, 13 coma 17, 14 coma 16, 15 coma 15, 16 coma 14, coma 16, 16 coma 14, 17 coma 13, 18 coma 12, 19 coma 11, 20 coma 10, 21 coma 9, 22 coma 8, 23 coma 7, 24 coma 6, 25 coma 5, 26 coma 4, 27 coma 3, 28 coma 2, 29 coma 1, 30 coma 0.

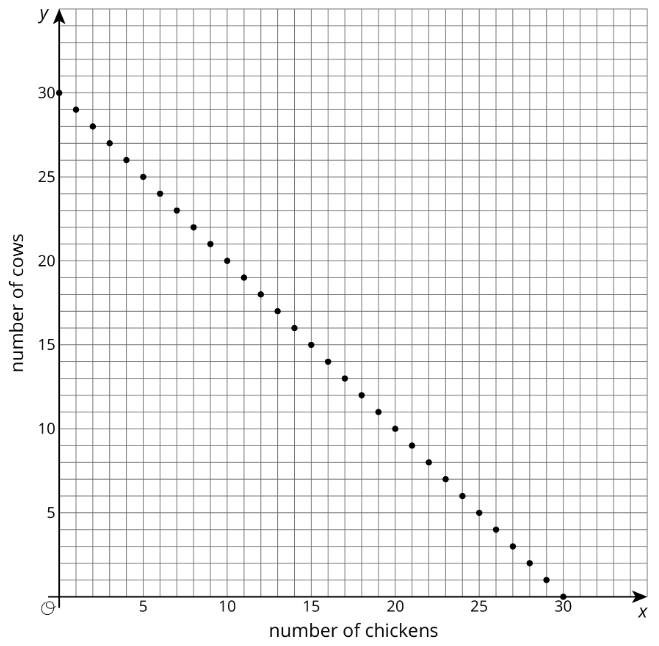
Si la granja tiene 30 pollos y vacas, y hay 82 patas de pollo y vaca todas juntas, entonces ¿cuántas gallinas y cuántas vacas podría tener la granja?

(De la Unidad 4.3.2)

tiempo desde el inicio (segundos)	distancia desde el inicio (metros)
\(6\)	\(36\)
\(9\)	\(54\)

número de pollos (\(x\))	número de vacas (\(y\))
\ (x\)) ">\(35\)	\ (y\)) ">
\ (x\)) ">\(7\)	\ (y\)) ">
\ (x\)) ">	\ (y\)) ">\(10\)
\ (x\)) ">\(19\)	\ (y\)) ">
\ (x\)) ">	\ (y\)) ">\(5\)