Saltar al contenido principal
LibreTexts Español

4.3.6: Escritura de Sistemas de Ecuaciones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118692

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Escribamos sistemas de ecuaciones a partir de situaciones del mundo real.

    Ejercicio\(\PageIndex{1}\): How Many Solutions? Matching

    Coincidir cada sistema de ecuaciones con el número de soluciones que tiene el sistema.

    1. \(\left\{\begin{array}{l}{y=-\frac{4}{3}x+4}\\{y=-\frac{4}{3}x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=4x-5}\\{y=-2x+7}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{2x+3y=8}\\{4x+6y=17}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{y=5x-15}\\{y=5(x-3)}\end{array}\right.\)
    1. Sin soluciones
    2. Una solución
    3. Infinitamente muchas soluciones

    Ejercicio\(\PageIndex{2}\): Situations and Systems

    Para cada situación:

    • Crear un sistema de ecuaciones.
    • Entonces, sin resolver, interpreta lo que la solución al sistema te diría sobre la situación.
    1. La familia de Lin sale a dar un paseo en bicicleta cuando su papá se detiene para tomar una foto del paisaje. Le dice al resto de la familia que siga adelante y que se pondrá al día. El papá de Lin pasa 5 minutos tomando la foto y luego cabalga a 0.24 millas por minuto hasta que se encuentra con el resto de la familia más adelante a lo largo del carril bici. Lin y el resto viajaban a 0.18 millas por minuto.
    2. Noah está planeando un viaje en kayak. Renta de Kayak A cobra una tarifa base de $15 más $4.50 por hora. Kayak Rental B cobra una tarifa base de $12.50 más $5 por hora.
    3. Diego está haciendo un lote grande de repostería. La receta exige 3 fresas por cada manzana. Diego usó 52 frutos todos juntos.
    4. La harina cuesta $0.80 por libra y el azúcar cuesta $0.50 por libra. Un pedido de harina y azúcar pesa 15 libras y cuesta $9.00.

    Ejercicio\(\PageIndex{3}\): Info Gap: Racing and Play Tickets

    Tu profesor te dará ya sea una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu pareja.

    Si tu profesor te da la tarjeta de problemas:

    1. Lee silenciosamente tu tarjeta y piensa en qué información necesitas para poder responder a la pregunta.
    2. Pídele a tu pareja la información específica que necesites.
    3. Explique cómo está utilizando la información para resolver el problema.
      Continúa haciendo preguntas hasta que tengas la información suficiente para resolver el problema.
    4. Comparte la tarjeta de problemas y resuelve el problema de forma independiente.
    5. Lee la tarjeta de datos y discute tu razonamiento.

    Si tu profesor te da la tarjeta de datos:

    1. Lee silenciosamente tu tarjeta.
    2. Pregúntale a tu pareja “¿Qué información específica necesitas?” y esperar a que pidan información.
      Si tu pareja solicita información que no esté en la tarjeta, no hagas los cálculos por ellos. Diles que no tienes esa información.
    3. Antes de compartir la información, pregunta “¿Por qué necesitas esa información? ” Escucha el razonamiento de tu pareja y haz preguntas aclaratorias.
    4. Lea la tarjeta del problema y resuelva el problema de forma independiente.
    5. Comparte la tarjeta de datos y discute tu razonamiento.

    Ejercicio\(\PageIndex{4}\): Solving Systems Practice

    Aquí hay muchos sistemas de ecuaciones:

    • \(\left\{\begin{array}{l}{y=-2x+6}\\{y=x-3}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{y=5x-4}\\{y=4x+12}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{y=\frac{2}{3}x-4}\\{y=-\frac{4}{3}x+9}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{4y+7x=6}\\{4y+7x=-5}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{y=x-6}\\{x=6+y}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{y=0.24x}\\{y=0.18x+0.9}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{y=4.5x+15}\\{y=5x+12.5}\end{array}\right.\)
    • \(\left\{\begin{array}{l}{y=3x}\\{+y=52}\end{array}\right.\)
    1. Sin resolver, identifica 3 sistemas que creas que serían los menos difíciles de resolver para ti y 3 sistemas que crees que serían los más difíciles. Esté preparado para explicar su razonamiento.
    2. Elija 4 sistemas para resolver. Al menos uno debería ser de tu lista de “menos difíciles” y uno debería ser de tu lista de “más difíciles”.

    Resumen

    Hemos aprendido a resolver muchos tipos de sistemas de ecuaciones utilizando álgebra que serían difíciles de resolver graficando. Por ejemplo, mira

    \[\left\{\begin{array}{l}{y=2x-3}\\{x+2y=7}\end{array}\right.\nonumber\]

    La primera ecuación dice que\(y=2x-3\), así donde quiera que veamos\(y\), podemos sustituir la expresión\(2x-3\) en su lugar. Entonces la segunda ecuación se convierte\(x+2(2x-3)=7\).

    Podemos resolver para\(x\):

    \[\begin{aligned} x+4x-6&=7 &\text{distributive property} \\ 5x-6&=7 &\text{combine like terms} \\ 5x&=13 &\text{add 6 to each side}\\ x&=\frac{13}{5} &\text{multiply each side by} \frac{1}{5}\end{aligned}\nonumber\]

    Sabemos que el\(y\) valor para la solución es el mismo para cualquiera de las dos ecuaciones, por lo que podemos usar cualquiera de las dos ecuaciones para resolverla. Usando la primera ecuación, obtenemos:

    \[\begin{aligned} y&=2\left(\frac{13}{5}\right)-3 &\text{substitute x=}\frac{13}{5}\text{into the equation} \\ y&=\frac{26}{5}-3 &\text{multiply } 2\left(\frac{13}{5}\right)\text{ to make }\frac{26}{5} \\ y&=\frac{26}{5}-\frac{15}{5} &\text{rewrite 3 as }\frac{15}{5} \\ y&=\frac{11}{5}\end{aligned}\nonumber\]

    Si sustituimos\(x=\frac{13}{5}\) en la otra ecuación\(x+2y=7\),, obtenemos el mismo\(y\) valor. Entonces la solución al sistema es\(\left(\frac{13}{5},\frac{11}{5}\right)\).

    Hay muchos tipos de sistemas de ecuaciones que aprenderemos a resolver en futuros grados, como

    \[\left\{\begin{array}{l}{2x+3y=6}\\{-x+2y=3}\end{array}\right.\nonumber\]

    O incluso

    \[\left\{\begin{array}{l}{y=x^{2}+1}\\{y=2x+3}\end{array}\right.\nonumber\]

    Entradas en el glosario

    Definición: Sistema de ecuaciones

    Un sistema de ecuaciones es un conjunto de dos o más ecuaciones. Cada ecuación contiene dos o más variables. Queremos encontrar valores para las variables que hagan verdaderas todas las ecuaciones.

    Estas ecuaciones conforman un sistema de ecuaciones:

    \[\left\{\begin{array}{l}{x+y=-2}\\{x-y=12}\end{array}\right.\nonumber\]

    La solución a este sistema es\(x=5\) y\(y=-7\) porque cuando estos valores son sustituidos por\(x\) y\(y\), cada ecuación es verdadera:\(5+(-7)=-2\) y\(5-(-7)=12\).

    Practica

    Ejercicio\(\PageIndex{5}\)

    Kiran y su primo trabajan durante el verano para una empresa de paisajismo. El primo de Kiran lleva más tiempo trabajando para la compañía, por lo que su paga es 30% más que la de Kiran. La semana pasada su primo trabajó 27 horas, y Kiran trabajó 23 horas. Juntos, ganaron 493.85 dólares. ¿Cuál es el pago por hora de Kiran? Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{6}\)

    Decidir qué historia puede ser representada por el sistema de ecuaciones\(y=x+6\) y\(x+y=100\). Explica tu razonamiento.

    1. El maestro de Diego escribe una prueba por valor de 100 puntos. Hay 6 preguntas de opción múltiple más que preguntas de respuesta corta.
    2. Lin y su primo menor miden sus alturas. Se dan cuenta de que Lin es 6 pulgadas más alto, y sus alturas suman exactamente 100 pulgadas.

    Ejercicio\(\PageIndex{7}\)

    Clare y Noah juegan un juego en el que ganan la misma cantidad de puntos por cada gol y pierden la misma cantidad de puntos por cada penalti. Clare hace 6 goles y 3 penales, terminando el juego con 6 puntos. Noé gana 8 goles y 9 penales y termina el juego con\(-22\) puntos.

    1. Escribe un sistema de ecuaciones que describa los resultados de Clare y Noé. Se usa\(x\) para representar el número de puntos para un gol y\(y\) para representar el número de puntos para una penalización.
    2. Resuelve el sistema. ¿Qué significa tu solución?

    Ejercicio\(\PageIndex{8}\)

    Resolver:

    \[\left\{\begin{array}{l}{y=6x-8}\\{y=-3x+10}\end{array}\right.\nonumber\]

    (De la Unidad 4.3.5)

    Ejercicio\(\PageIndex{9}\)

    1. Estimar las coordenadas del punto donde se encuentran las dos líneas.

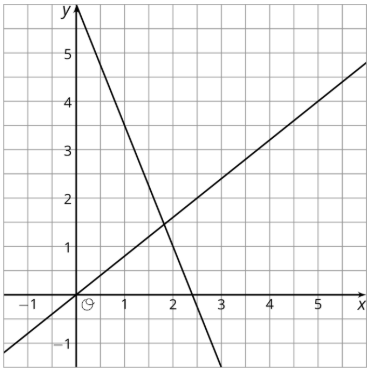
    clipboard_e11e5e375d307c01dcc1119345835750b.png
    Figura\(\PageIndex{1}\): La gráfica de dos líneas que se cruzan en el plano XY. Escala negativa del 1 al 5 en ambos ejes. La primera línea se inclinó hacia arriba y hacia la derecha, cruza el eje y en 0, y pasa por el punto 3 coma 2. La segunda línea se inclinó hacia abajo y hacia la derecha, cruza el eje y en 6, y pasa por el punto 2 coma 1.

    2. Elija dos ecuaciones que conforman el sistema representado por la gráfica.

    1. \(y=\frac{5}{4}x\)
    2. \(y=6-2.5x\)
    3. \(y=2.5x+6\)
    4. \(y=6-3x\)
    5. \(y=0.8x\)

    Ejercicio\(\PageIndex{10}\)

    Resuelve el sistema de ecuaciones y confirma la exactitud de tu estimación.

    (De la Unidad 4.3.4)

    This page titled 4.3.6: Escritura de Sistemas de Ecuaciones is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.