4.3.5: Resolver más sistemas

Lección

Resolvamos sistemas de ecuaciones.

Ejercicio\(\PageIndex{1}\): Algebra Talk: Solving Systems Mentally

Resuelve estos sin anotar nada:

\[\left\{\begin{array}{l}{x=5}\\{y=x-7}\end{array}\right.\nonumber\]

\[\left\{\begin{array}{l}{y=4}\\{y=x+3}\end{array}\right.\nonumber\]

\[\left\{\begin{array}{l}{x=8}\\{y=-11}\end{array}\right.\nonumber\]

Ejercicio\(\PageIndex{2}\): Challenge Yourself

Aquí hay muchos sistemas de ecuaciones:

1. \(\left\{\begin{array}{l}{y=4}\\{x=-5y+6}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{y=7}\\{x=3y-4}\end{array}\right.\)
3. \(\left\{\begin{array}{l}{y=\frac{3}{2}x+7}\\{x=-4}\end{array}\right.\)
4. \(\left\{\begin{array}{l}{y=-3x+10}\\{y=-2x+6}\end{array}\right.\)
5. \(\left\{\begin{array}{l}{y=-3x-5}\\{y=4x+30}\end{array}\right.\)
6. \(\left\{\begin{array}{l}{y=3x-2}\\{y=-2x+8}\end{array}\right.\)
7. \(\left\{\begin{array}{l}{y=3x}\\{x=-2y+56}\end{array}\right.\)
8. \(\left\{\begin{array}{l}{x=2y-15}\\{y=-2x}\end{array}\right.\)
9. \(\left\{\begin{array}{l}{3x+4y=10}\\{x=2y}\end{array}\right.\)
10. \(\left\{\begin{array}{l}{y=3x+2}\\{2x+y=47}\end{array}\right.\)
11. \(\left\{\begin{array}{l}{y=-2x+5}\\{2x+3y=31}\end{array}\right.\)
12. \(\left\{\begin{array}{l}{x+y=10}\\{x=2y+1}\end{array}\right.\)

1. Sin resolver, identifica 3 sistemas que creas que serían los menos difíciles de resolver y 3 sistemas que crees que serían los más difíciles de resolver. Esté preparado para explicar su razonamiento.
2. Elija 4 sistemas para resolver. Al menos uno debería ser de tu lista de “menos difíciles” y uno debería ser de tu lista de “más difíciles”.

Ejercicio\(\PageIndex{3}\): Five Does Not Equal Seven

Tyler estaba mirando este sistema de ecuaciones:

\[\left\{\begin{array}{l}{x+y=5}\\{x+y=7}\end{array}\right.\nonumber\]

Dijo: “Con solo mirar el sistema, puedo ver que no tiene solución. Si agrega dos números, esa suma no puede ser igual a dos números diferentes”.

¿Estás de acuerdo con Tyler?

¿Estás listo para más?

En rectángulo\(ABCD\), el lado\(AB\) es de 8 centímetros y el lado\(BC\) es de 6 centímetros. \(F\)es un punto sobre\(BC\) y\(E\) es un punto en\(AB\). El área del triángulo\(DFC\) es de 20 centímetros cuadrados, y el área del triángulo\(DEF\) es de 16 centímetros cuadrados. ¿Cuál es el área del triángulo\(AED\)?

Resumen

Cuando tenemos un sistema de ecuaciones lineales donde una de las ecuaciones es de la forma\(y=\text{ [stuff]}\) o\(x=\text{ [stuff]}\), podemos resolverlo algebraicamente mediante el uso de una técnica llamada sustitución. La idea básica es reemplazar una variable con una expresión a la que es igual (por lo que la expresión es como un sustituto de la variable). Por ejemplo, comencemos con el sistema:

\[\left\{\begin{array}{l}{y=5x}\\{2x-y=9}\end{array}\right.\nonumber\]

Como sabemos eso\(y=5x\), podemos sustituir\(5x\)\(y\) en la ecuación\(2x-y=9\),

\(2x-(5x)=9\),

y luego resolver la ecuación para\(x\),

\(x=-3\).

Podemos encontrar\(y\) usando cualquiera de las ecuaciones. Usando el primero:\(y=5\cdot -3\). Entonces

\((-3,15)\)

es la solución a este sistema. Podemos verificar esto observando las gráficas de las ecuaciones en el sistema:

Figura\(\PageIndex{1}\): Gráfica de dos líneas, origen O, con cuadrícula. Eje horizontal, x, escala negativa 10 a 10, por 2's. Eje vertical, y, escala negativa 30 a 30, por 10's. Una línea está etiquetada como y es igual a 5 x. Otra línea está etiquetada como 2 x menos y es igual a 9. Las líneas se cruzan en negativo 3 coma negativo 15.

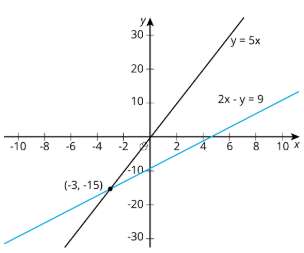
¡Seguro! Se cruzan en\((-3,-15)\).

No lo sabíamos en ese momento, pero en realidad también estábamos usando la sustitución en la última lección. En esa lección, miramos el sistema

\[\left\{\begin{array}{l}{y=2x+6}\\{y=-3x-4}\end{array}\right.\nonumber\]

y\(2x+6\) sustituimos\(y\) en la segunda ecuación para obtener\(2x+6=-3x-4\). ¡Vuelve y comprueba por ti mismo!

Entradas en el glosario

Definición: Sistema de ecuaciones

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones. Cada ecuación contiene dos o más variables. Queremos encontrar valores para las variables que hagan verdaderas todas las ecuaciones.

Estas ecuaciones conforman un sistema de ecuaciones:

\[\left\{\begin{array}{l}{x+y=-2}\\{x-y=12}\end{array}\right.\nonumber\]

La solución a este sistema es\(x=5\) y\(y=-7\) porque cuando estos valores son sustituidos por\(x\) y\(y\), cada ecuación es verdadera:\(5+(-7)=-2\) y\(5-(-7)=12\).

Practica

Ejercicio\(\PageIndex{4}\)

Resolver:

\[\left\{\begin{array}{l}{y=6x}\\{4x+y=7}\end{array}\right.\nonumber\]

Ejercicio\(\PageIndex{5}\)

Resolver:

\[\left\{\begin{array}{l}{y=3x}\\{x=-2y+70}\end{array}\right.\nonumber\]

Ejercicio\(\PageIndex{6}\)

1. \(y=-1.5x+6\)
2. \(y=-1.5x\)
3. \(2y=-3x+6\)
4. \(2y+3x=6\)
5. \(y=-2x+3\)

Ejercicio\(\PageIndex{7}\)

El sistema\(x=6y=4\), no\(3x-18y=4\) tiene solución.

1. Cambiar una constante o coeficiente para hacer un nuevo sistema con una sola solución.
2. Cambiar una constante o coeficiente para hacer un nuevo sistema con un número infinito de soluciones.

Ejercicio\(\PageIndex{8}\)

Coincidir cada gráfica con su ecuación.

Figura\(\PageIndex{2}\): Cuatro gráficas, cada una con una línea en el plano x y. Gráfica A. La línea cruza el eje y en 3 y pasa por el punto negativo 1 coma 1. Gráfica B. La línea cruza el eje y en negativo 3 y pasa por el punto 1 coma negativo 1. Gráfica C. La línea cruza el eje y en 3 y pasa por el punto 1 coma 1. Gráfica D. La línea cruza el eje y en negativo 3 y pasa por el punto negativo 1 coma negativo 1.

1. \(y=2x+3\)
2. \(y=-2x+3\)
3. \(y=2x-3\)
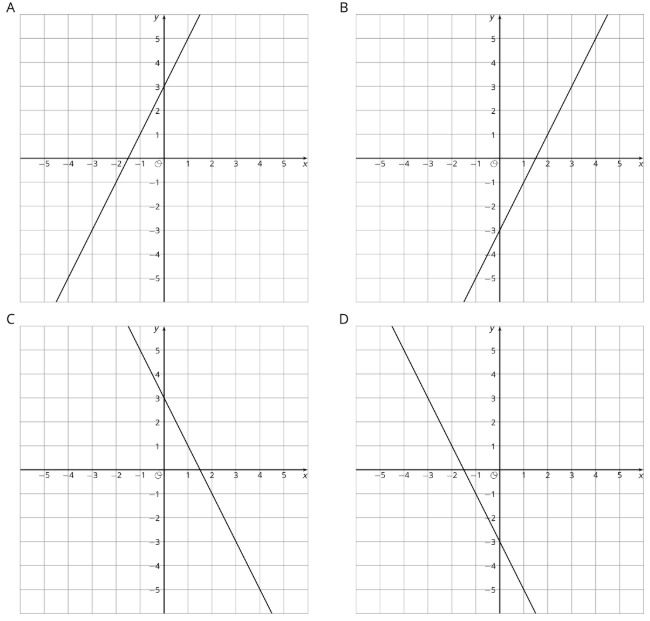
4. \(y=-2x-3\)

(De la Unidad 3.3.3)

Ejercicio\(\PageIndex{9}\)

Aquí hay dos puntos:\((-3,4)\),\((1,7)\). ¿Cuál es la pendiente de la línea entre ellos?

1. \(\frac{4}{3}\)
2. \(\frac{3}{4}\)
3. \(\frac{1}{6}\)
4. \(\frac{2}{3}\)

(De la Unidad 3.3.2)